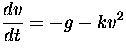 when
when 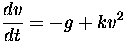 when
when
I did some more reading (N. de Mestre, The Mathematics of Projectiles
in Sport, Cambridge University Press 1990), and it turns out that the
physics of pop flies is rather more complicated than what I told you.
For balls and other objects used in most sports, air resistance is proportional
to speed only at extremely low speeds. At more typical speeds, it is
essentially proportional to the square of the speed. Since the direction
of the air resistance force is opposite to the velocity, this means the
differential equation for velocity can be written in the form
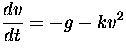 when
when ![]() ,
,
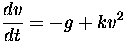 when
when ![]() , where k is a positive
constant.
In the case of a baseball, it appears that k is approximately
.0076 m-1.
, where k is a positive
constant.
In the case of a baseball, it appears that k is approximately
.0076 m-1.
The terminal velocity is calculated by setting the right side of the
equation for dv/dt to 0 and solving for v. Of course this requires
v < 0, so ![]() /sec approximately (but see below).
/sec approximately (but see below).
Now let's reconsider the pop fly. It starts out going up, with v = v0 at t = 0. The DE is nonlinear, but it is separable:
![]()
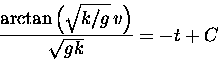
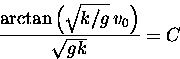
![]()
Note that v=0 when t=C, i.e. the ball reaches its maximum height
at time 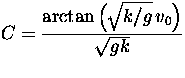 .
Since there will be other constants to consider later, I'll rename
this as t1 (and use C again for other constants of integration later).
.
Since there will be other constants to consider later, I'll rename
this as t1 (and use C again for other constants of integration later).
How high will the ball get? We must integrate v:
![]()
![]()
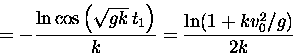
Now coming down, the equation is again separable, and we have
![]()
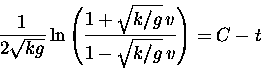
0 = C - t1
(the last equation coming from substituting t = t1, v = 0). We can solve for v: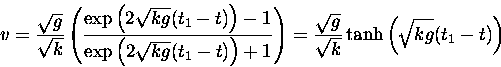
![]()
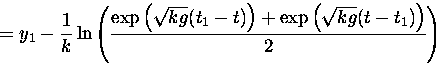
The ball comes back to y=0 at t = t2 > t1 where
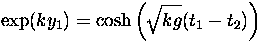 , but using the equation
for y1 we have
, but using the equation
for y1 we have ![]() . Thus
finally we obtain
. Thus
finally we obtain
![]()
For our 7-second pop fly, we solve t2 = 7 numerically for v0, obtaining v0 = 43.7 m/sec approximately. Moreover, with this value of v0 the maximum height of the ball is y1 = 59.8 m approximately. After all that, the numbers were not very different from those we obtained with linear air resistance.
However, there is a complication: at a certain critical speed, the flow of air past the ball becomes turbulent, and it turns out that this reduces the air resistance by about 56%. By the way, one reason that golf balls have dimples is that this reduces the critical speed. A smooth golf ball's critical speed would be above the typical speed of a drive, while a dimpled golf ball's is below. Thus a dimpled golf ball goes farther. As far as I know, for a baseball the critical speed is about 30 m/sec. Thus a better model for the pop fly would use k = .0076 m/sec for |v| < 30 and k = .0033 m/sec for |v| > 30.
Let's reconsider the terminal velocity in this new model.
If the speed is less than the critical speed and the net force is 0,
as we saw ![]() /sec. It appears that this is faster
than the critical speed. If that's the case, we must look for the
terminal velocity in the turbulent regime, with k = .0033. There
we get
/sec. It appears that this is faster
than the critical speed. If that's the case, we must look for the
terminal velocity in the turbulent regime, with k = .0033. There
we get ![]() /sec approximately. It makes
quite a difference, especially if you're catching the ball: this is
nearly 122 miles per hour (compare to Nolan Ryan's record fastball
pitch of 100.9 miles per hour).
/sec approximately. It makes
quite a difference, especially if you're catching the ball: this is
nearly 122 miles per hour (compare to Nolan Ryan's record fastball
pitch of 100.9 miles per hour).
Matters would be even more interesting if the critical speed sC
was between
36 and 54.5 m/sec
(it might even be true for baseballs, because that
30 m/sec was a very inexact figure).
That would mean that there would be two possible
terminal velocities, -36 and -54.5. A ball that starts off with
v > -sC would approach velocity
-36 m/sec as
![]() ,
while one that starts with v < -sC would approach -54.5.
,
while one that starts with v < -sC would approach -54.5.
If you started at exactly v = -sC it's not clear what would happen: the right side of the differential equation is not continuous there, so the existence and uniqueness theorem breaks down. Presumably this is the fault of our model rather than a feature of physics, and the transition to turbulent flow is not really discontinuous. If so, what happens at v = -sC would actually be an unstable equilibrium: if the velocity was exactly -sC it would be constant, but if otherwise it would either speed up or slow down and approach one of the stable equilibria.
As for our 7-second pop fly, it turns out not to exceed the critical speed on the way down. Thus there are three phases of its flight to consider: rising with speed greater than sC, rising with speed less than sC, and falling. The initial velocity v0 turns out to be about 39.7 m/sec, and the maximum height 59.3 m.