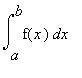 , where
, where
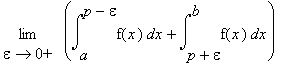 .
.
Function: PVInt - numerical principal value integral
Calling sequence:
PVint(f, x=a..b, p)
Parameters:
f - the integrand, expression in one variable x
x - name
a, b - real constants, the endpoints of the integration
p - real constant, location of a singularity in the interval of integration
Description:
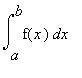 , where
, where
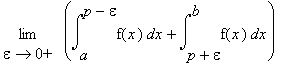 .
.
Examples:
> PVInt(tan(x), x = 0 .. 2, Pi/2);
![]()
This one could have been integrated symbolically.
> int(tan(x),x=0..2,CauchyPrincipalValue);
![]()
> evalf(%);
![]()
The singularity at
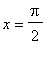 would cause ordinary numerical integration to fail.
would cause ordinary numerical integration to fail.
> evalf(Int(tan(x),x=0..2));
Error, (in evalf/int) numeric exception: invalid operation
The next one can not be integrated symbolically: presumably there is no closed form for the integral.
> int(1/(x+sin(x)),x);
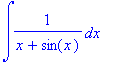
> PVInt(1/(x+sin(x)),x=-1..2,0);
![]()
The next one diverges.
> PVInt(1/(sin(x)^3+x^4), x=-1..2, 0);
![]()
The location of the singularity must be known exactly. A floating-point approximation would not be enough.
> p0:= fsolve(exp(x)-3*x,x=0..1);
![]()
> PVInt(1/(exp(x)-3*x),x=0..1,p0);
Error, (in evalf/int) unable to handle singularity
Since it depends on finding a finite number of terms with negative exponents in the Laurent series, PVInt will not work with singularities that are essential or non-isolated. For example, the following principal value integral is 0 by symmetry, but PVInt can't evaluate it.
> PVInt(exp(1/x)-exp(-1/x),x=-1..1,0);
Error, (in numapprox[laurent]) unable to compute Laurent series
See also:
int , int[numeric]
Maple Advisor Database R. Israel, 2000