Triple integral

Scroll down to the bottom to view the interactive graph.

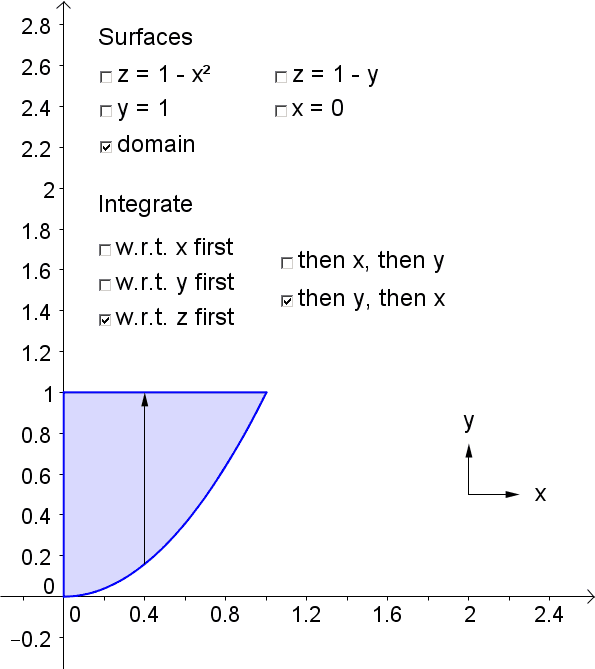
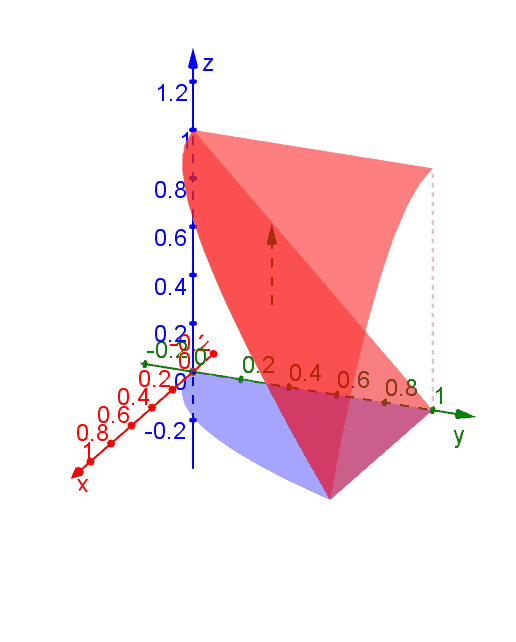
We consider the triple integral \[\iiint_E f(x,y,z) \,dV\] where \(E\) is the solid bounded by \(z = 1-x^2\), \(z = 1-y\), \(y = 1\) and \(x = 0\). There are six ways to write this triple integral as an interated integral in Cartesian coordinates: \[\int_0^1 \int_{1-z}^1 \int_0^{\sqrt{1-z}} f(x,y,z) \,dx \,dy \,dz\] \[\int_0^1 \int_{1-y}^1 \int_0^{\sqrt{1-z}} f(x,y,z) \,dx \,dz \,dy\] \[\int_0^1 \int_0^{\sqrt{1-z}} \int_{1-z}^1 f(x,y,z) \,dy \,dx \,dz\] \[\int_0^1 \int_0^{1-x^2} \int_{1-z}^1 f(x,y,z) \,dy \,dz \,dx\] \[\int_0^1 \int_0^{\sqrt{y}} \int_{1-y}^{1-x^2} f(x,y,z) \,dz \,dx \,dy\] \[\int_0^1 \int_{x^2}^1 \int_{1-y}^{1-x^2} f(x,y,z) \,dz \,dy \,dx\]

To view the interactive graph:

1. Make sure you have the latest version of Java 7 installed in your computer. Tablets and smartphones are not supported.
2. Download this file, tripleintegral.ggb.
3. Click here to open GeoGebra.
4. After you open GeoGebra, click "File" in the toolbar, then click "Open".
5. Choose the .ggb file you just downloaded and click the "Open" button.
6. Now you should be able to view the graph inside GeoGebra.

To rotate the graph, right click and drag.

Joseph Lo