Quadric surfaces

Scroll down to the bottom to view the interactive graph.

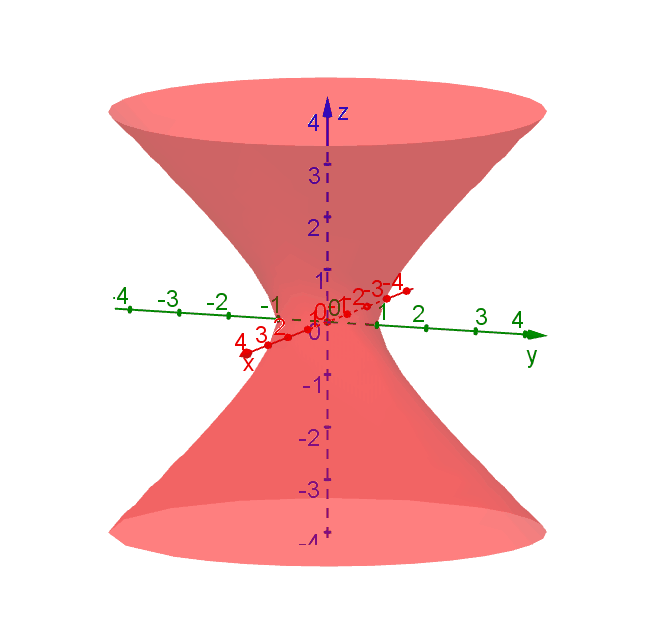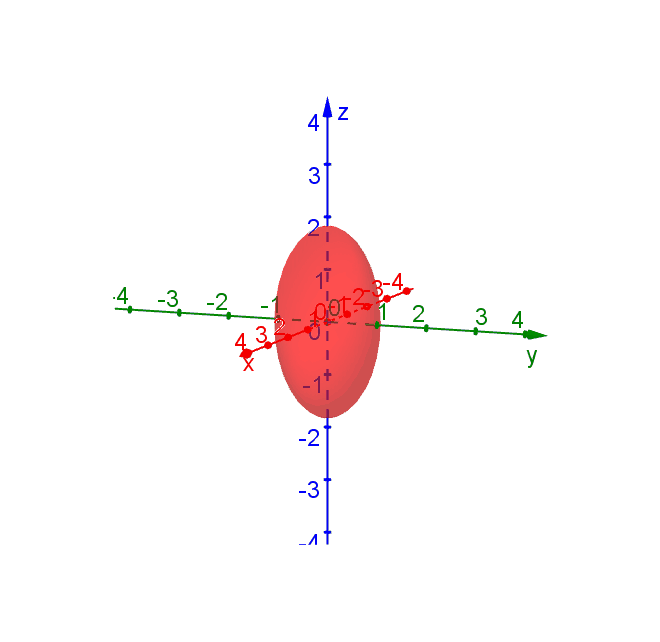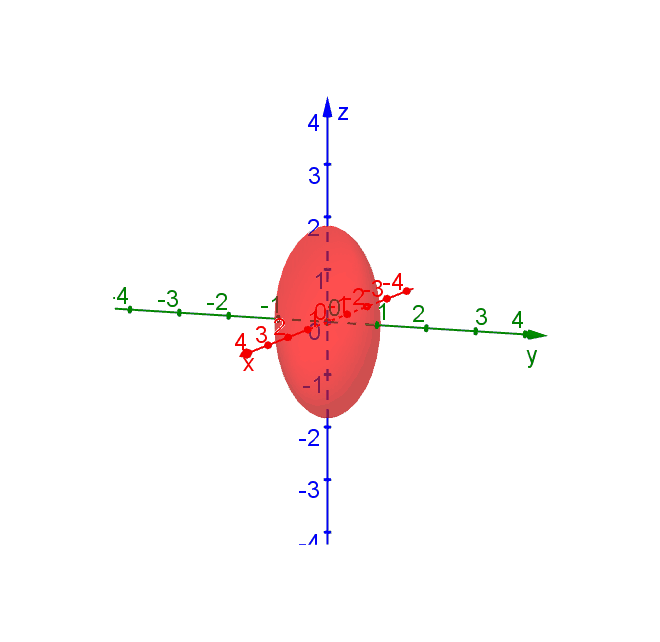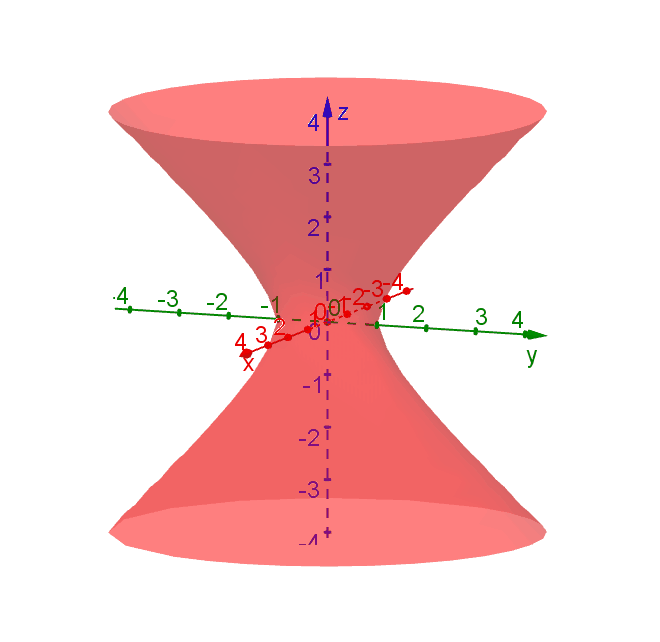
The signs of \(a\), \(b\) and \(c\) determine the shape of the quadric surface defined by \[ ax^2 + by^2 + cz^2 = 1.\] For example if we keep \(a\) and \(b\) positive, then a negative \(c\) gives a hyperboloid of one sheet with the centre axis along the \(z\)-axis, while positive \(c\) gives an ellipsoid (or a sphere if \(a = b = c\)). The following figure shows the transition from hyperboloid to ellipsoid by varying \(c\).

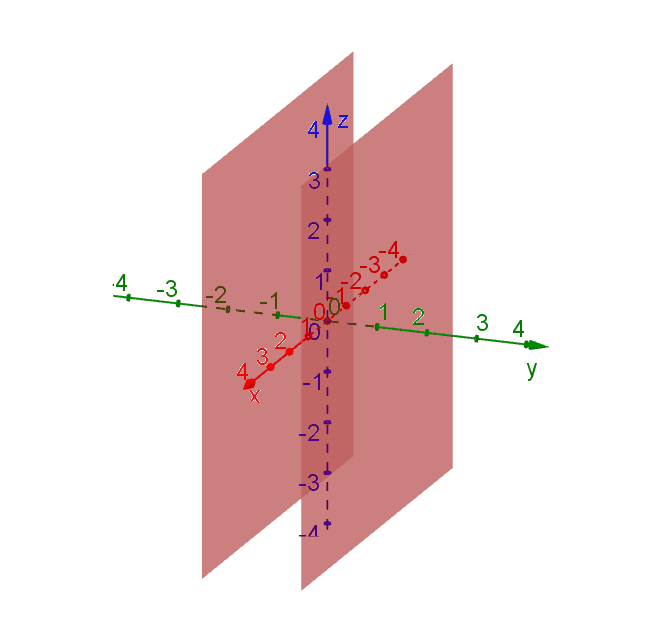
Can you determine the values of \(a\), \(b\) and \(c\) that give two parallel planes? You may explore using the interactive graph provided at the bottom of the page.

To view the interactive graph:

1. Make sure you have the latest version of Java 7 installed in your computer. Tablets and smartphones are not supported.
2. Download this file, quadric.ggb.
3. Click here to open GeoGebra.
4. After you open GeoGebra, click "File" in the toolbar, then click "Open".
5. Choose the .ggb file you just downloaded and click the "Open" button.
6. Now you should be able to view the graph inside GeoGebra.

To rotate the graph, right click and drag.

Joseph Lo