Scroll down to the bottom to view the interactive graph.
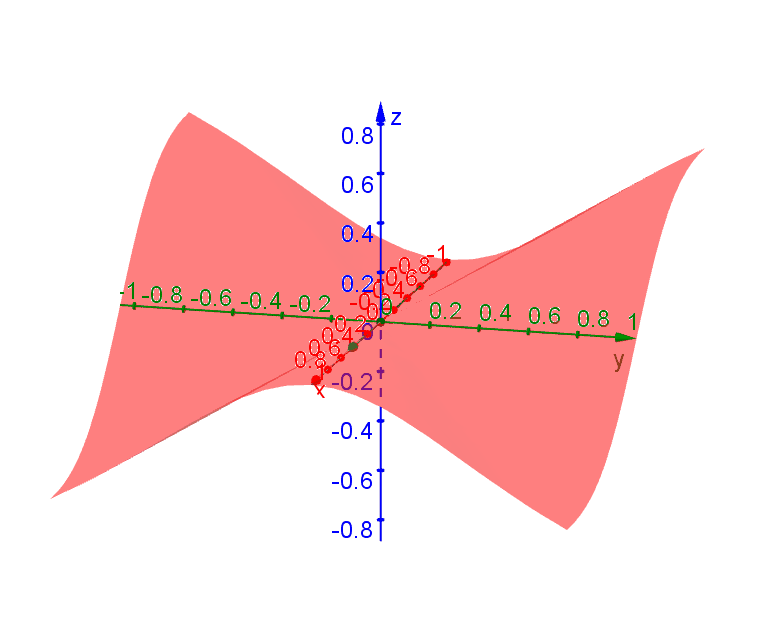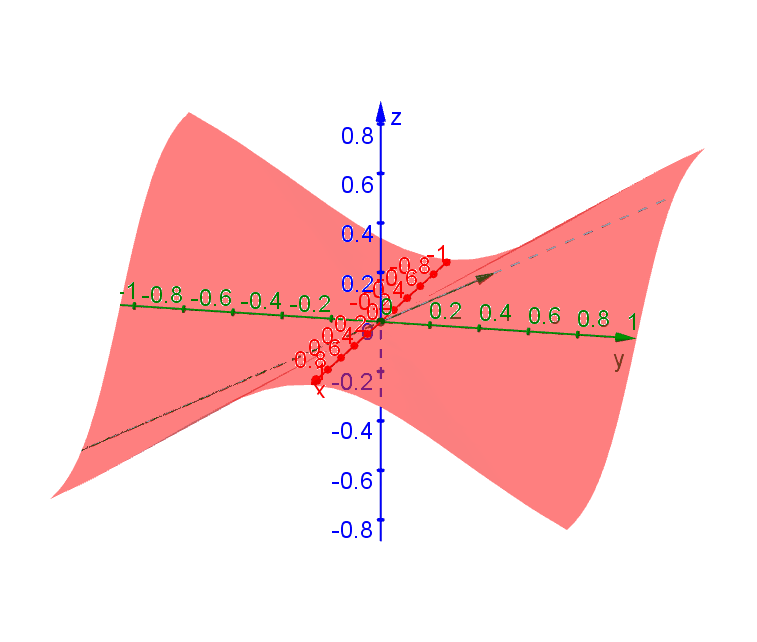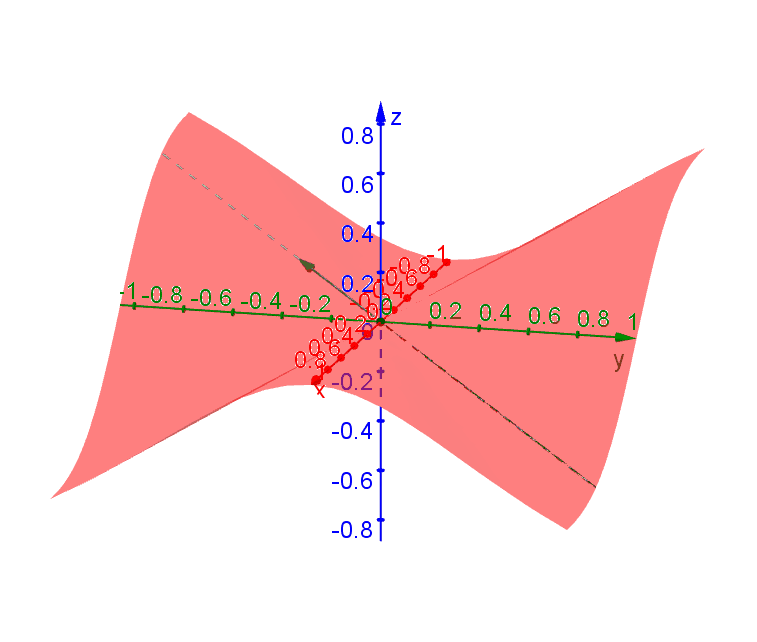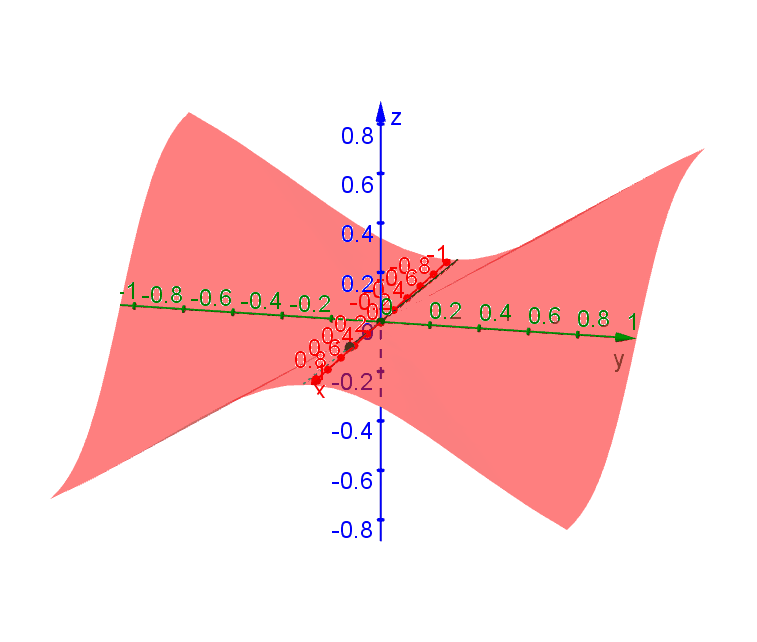
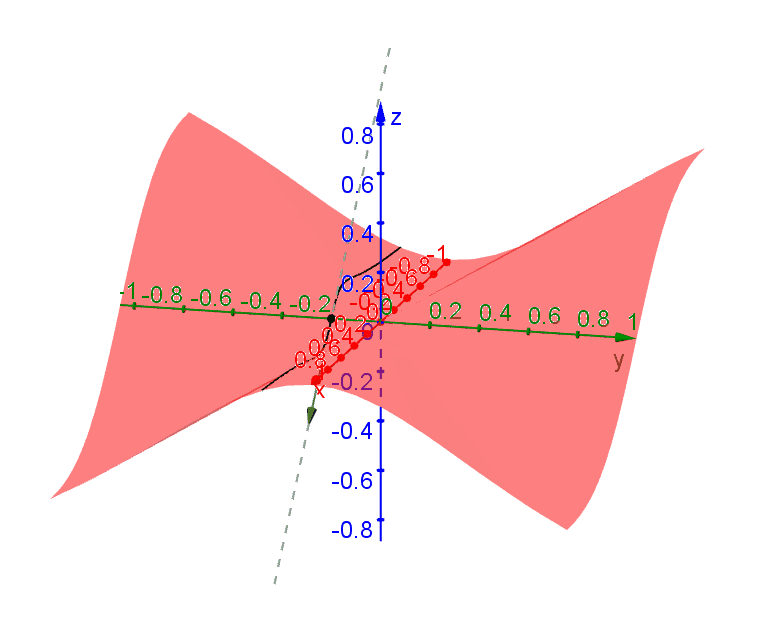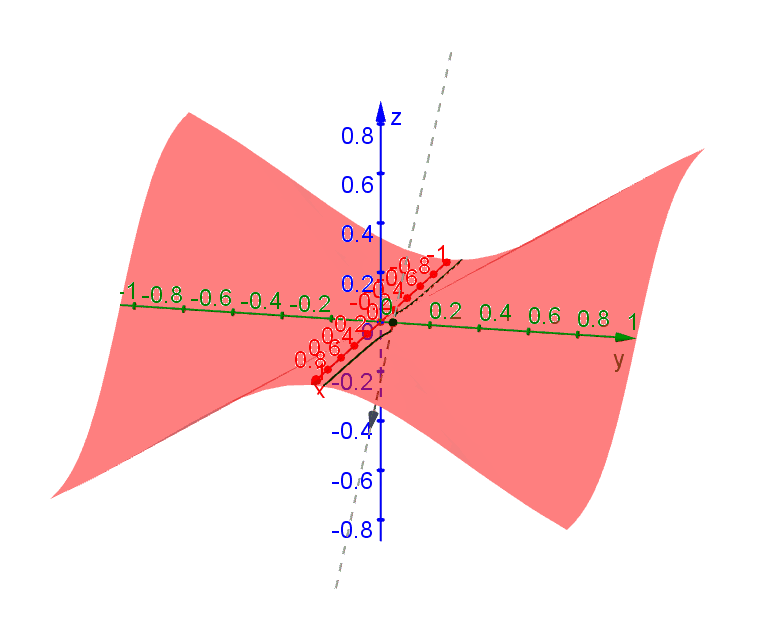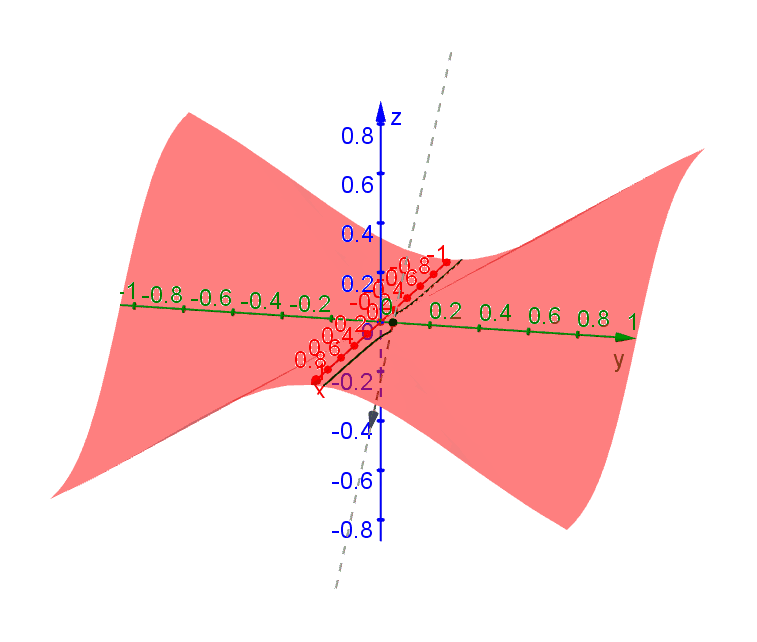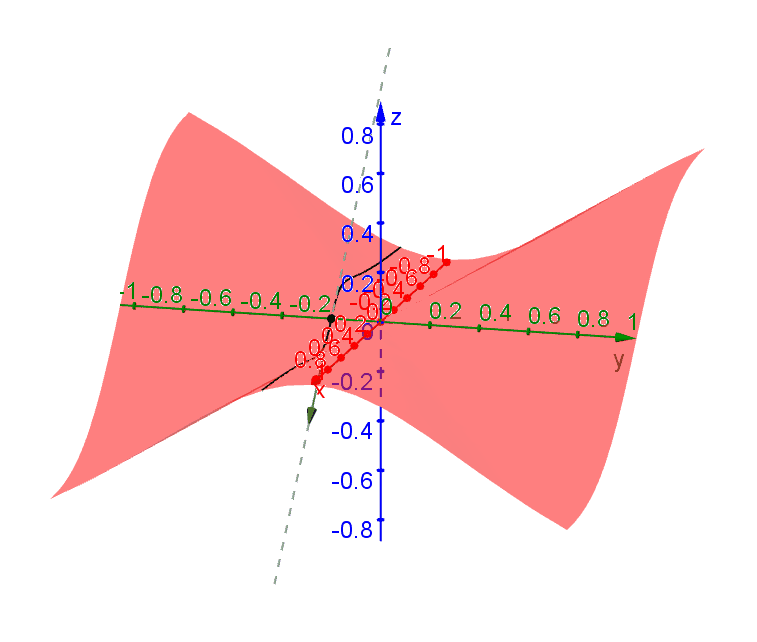
Consider the function \[f(x,y) = \begin{cases} -\dfrac{xy^2}{x^2+y^2} & x \neq 0 \\ 0 & x = 0\end{cases}\] Traces along all directions through \((0,0)\) have tangent lines (i.e. are differentiable) at \((0,0)\). However, there is no single plane that contains all these tangent lines. To see this, we can look at a few of these traces.
A trace passing through \((0,0)\) along the direction \(\theta\) (measured from the \(x\)-axis) can be represented by \((x,y) = (t\cos\theta,t\sin\theta)\). By plugging into \(f\) you get \[f(t\cos\theta,t\sin\theta) = -t\cos\theta\sin^2\theta\] after simplification. It follow that \(df/dt = -\cos\theta\sin^2\theta\).
Along the \(x\)-axis (\(y = 0, \theta = 0\)), \[\left.\dfrac{df}{dt}\right|_{t=0} = \left.\dfrac{\partial f}{\partial x}\right|_{(0,0)} = 0.\] Along the \(y\)-axis, (\(x = 0, \theta = \pi /2\)), \[\left.\dfrac{df}{dt}\right|_{t=0} = \left.\dfrac{\partial f}{\partial y}\right|_{(0,0)} = 0.\] Based on these partial derivatives, we may conclude that \(z = 0\) is the tangent plane. However, if we follow the trace along \(\theta = \pi/4\), then we find that the slope of this tangent line is \[\left.\dfrac{df}{dt}\right|_{t=0} = -\dfrac{1}{\sqrt{8}} \neq 0\] at \((0,0)\) and this tangent line certainly does not lie on the plane \(z = 0\).
The following diagram shows the tangent lines through \((0,0)\) along various directions.

Since there is no plane that can contain all these tangent lines, we conclude that a tangent plane at \((0,0)\) does not exist and \(f\) is not differentiable at \((0,0)\) even derivative exists in all directions.
If a function is non-differentiable at a point, then some of the partial derivatives must be discontinuous at that point. This is illustrated in the following diagram. For the above \(f\), \[\dfrac{\partial f}{\partial x} = \begin{cases} \dfrac{y^2(x^2-y^2)}{(x^2+y^2)^2} & (x,y) \neq (0,0) \\ 0 & (x,y) = (0,0)\end{cases}\] Along \(x = 0\), \[\left.\dfrac{\partial f}{\partial x}\right|_{(0,y)} = \begin{cases} -1 & y \neq 0 \\ 0 & y = 0 \end{cases}\] which says \(\partial f/\partial x\) is discontinuous at \((0,0)\).
To view the interactive graph:
To rotate the graph, right click and drag.
Joseph Lo