Critical Points of a differentiable function

Scroll down to the bottom to view the interactive graph.

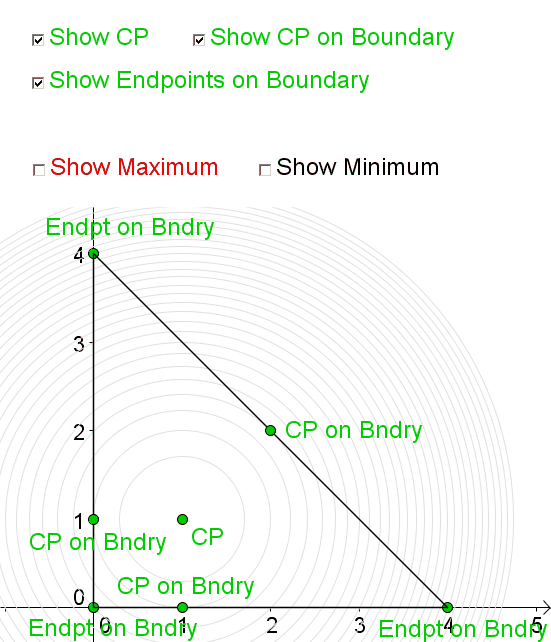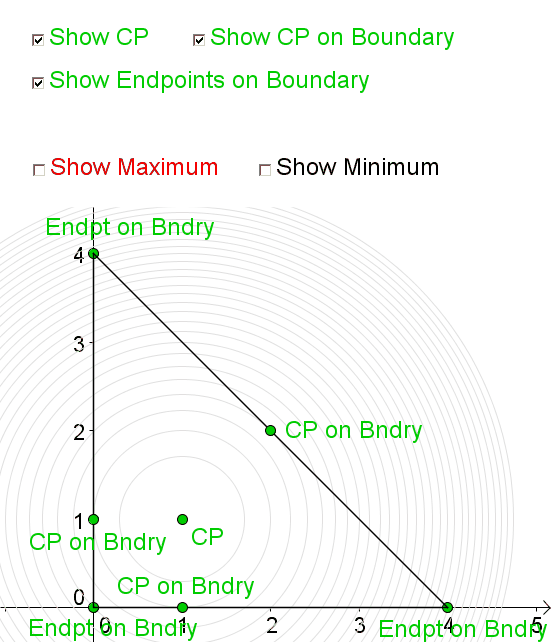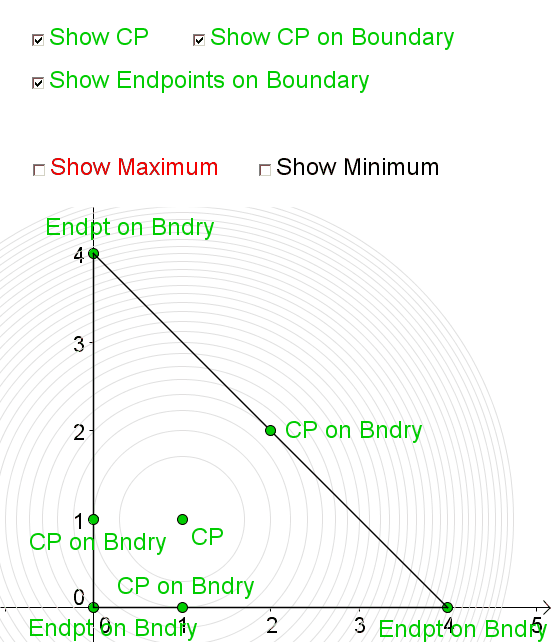
Consider the function \[f(x,y) = 1+x+y-\dfrac{1}{2}x^2-\dfrac{1}{2}y^2.\] We wish to find the absolute extrema of \(f(x,y)\) in the triangular region with vertices \((0,0)\), \((4,0)\) and \((0,4)\)

The following shows the critical points of \(f(x,y)\) both in the interior and on the boundary of the region as well as the endpoints of the boundary. The maxima and minima may occur at any of these points.

To view the interactive graph:

1. Make sure you have the latest version of Java 7 installed in your computer. Tablets and smartphones are not supported.
2. Download this file, maxmin.ggb.
3. Click here to open GeoGebra.
4. After you open GeoGebra, click "File" in the toolbar, then click "Open".
5. Choose the .ggb file you just downloaded and click the "Open" button.
6. Now you should be able to view the graph inside GeoGebra.

To rotate the graph, right click and drag.

Joseph Lo