Lines

 

Scroll down to the bottom to view the interactive graph.

 

Lines in 2D

A line in 2D is simple. You might have encountered equations of lines in different forms:

\(y = mx + b\)
   slope-\(y\)-intercept form
\(y - y_1 = m (x-x_1)\) or \(y = y_1 + m(x-x_1)\)
   point-slope form
\(Ax + By = C\)
   standard form, can also represent vertical lines
\(y - y_1 = \dfrac{y_2-y_1}{x_2-x_1} (x-x_1)\)
   two-point form
\(\dfrac{x}{a} + \dfrac{y}{b} = 1\)
   \(x/y\)-intercept form, not good for lines crossing the origin
  ... etc

Afterall, you are only dealing with one equation at a time. It is trivial (with minimial algebra) to show that all the above forms are equivalent to each other.

 

Lines in 3D

A lines in 3D space, however, is represented by a symmetric equation \[\dfrac{x-x_0}{a} = \dfrac{y-y_0}{b} = \dfrac{z-z_0}{c}.\] Noting that there are two equal signs, you are actually dealing with two separate equations: \[\dfrac{x-x_0}{a} = \dfrac{y-y_0}{b},\]\[ \dfrac{y-y_0}{b} = \dfrac{z-z_0}{c}.\] Each of these equations represents a plane, so the pair of equations together (or the symmetric equation) represents the intersection of the two planes (which is a line).

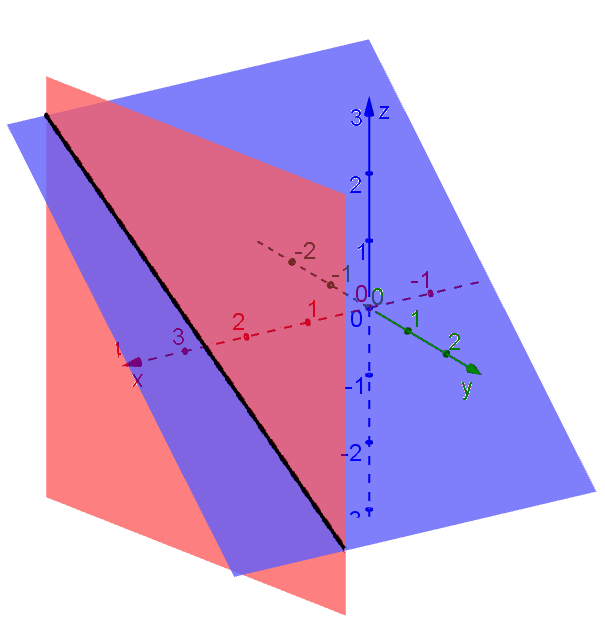
Let's think of an example (Example 2 in Section 12.5). The symmetric equation is given by \[\dfrac{x-2}{1} = \dfrac{y-4}{-5} = \dfrac{z+3}{4}.\] This is equivalent to the pair of equations: \[\dfrac{x-2}{1} = \dfrac{y-4}{-5}, \quad \text{or} \quad 5x+y = 14\tag{1}\] \[\dfrac{y-4}{-5} = \dfrac{z+3}{4}, \quad \text{or} \quad 4y + 5z = 1\tag{2}\]

Red: Plane (1); Blue: Plane (2)

The 3D graph shows the two planes, (1) and (2), and their intersection (which is the line described by the symmetric equation). Note that Plane (1) is parallel to the \(z\)-axis because there is no \(z\) in Eq. (1). For the same reason, Plane (2) is parallel to the \(x\)-axis.

Something you may ask: from the symmetric equation, can we extract an equation without \(y\) in it? Sure. A third equation can be found by equating the left and the right pieces, namely, \[\dfrac{x-2}{1} =\dfrac{z+3}{4}, \quad \text{or} \quad 4x-z = 11\tag{3}\]

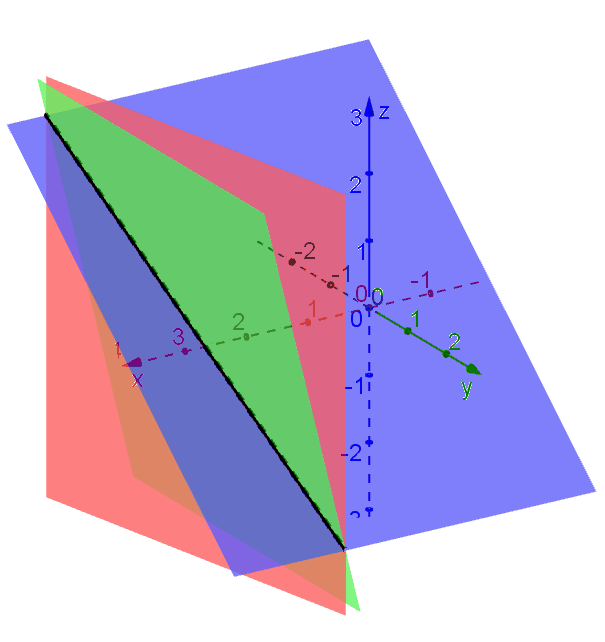
Red: Plane (1); Blue: Plane (2); Green: Plane (3)

All three planes intersect at the same line. You can define the line (intersection) by any two of the three planes. Indeed, there are infinitely many planes that crosses the same line. You can pick any two. For example, \[x+y+z=3 \tag{4}\] \[6x+2y+z=17\tag{5}\] together define the very same line.

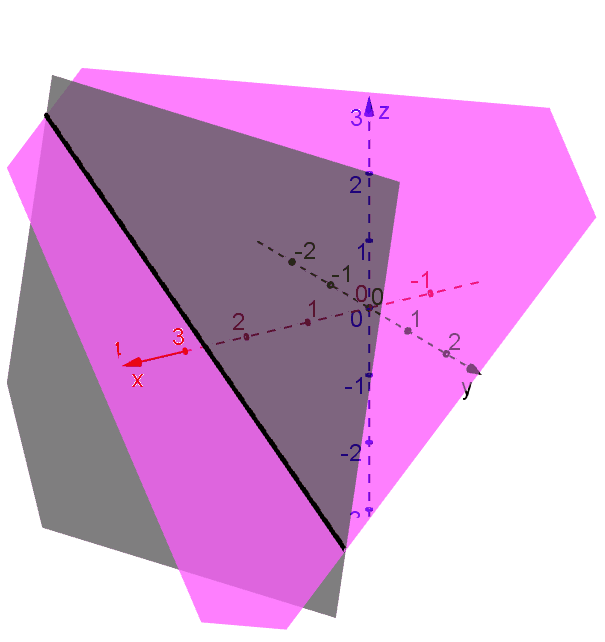
Magenta: Plane (4); Black: Plane (5)

 

Problem for you to solve:

Show that Eqs (4) and (5) together define the same line as the symmetric equation above.

 

 

To view the interactive graph:

  1. Make sure you have the latest version of Java 7 installed in your computer. Tablets and smartphones are not supported.
  2. Download this file, line.ggb.
  3. Click here to open GeoGebra.
  4. After you open GeoGebra, click "File" in the toolbar, then click "Open".
  5. Choose the .ggb file you just downloaded and click the "Open" button.
  6. Now you should be able to view the graph inside GeoGebra.

To rotate the graph, right click and drag.

Joseph Lo