Level surfaces

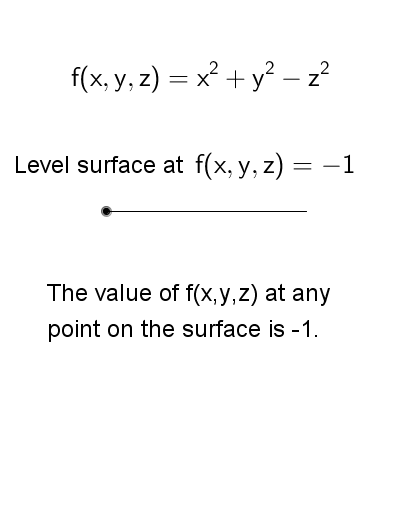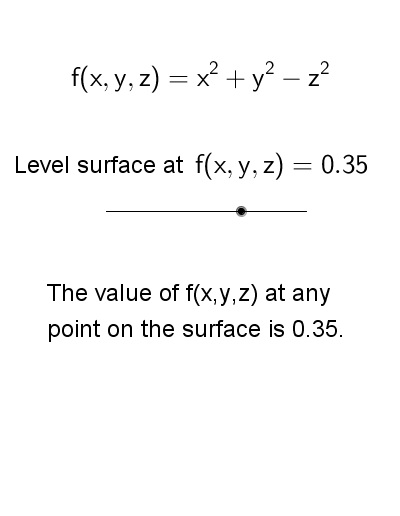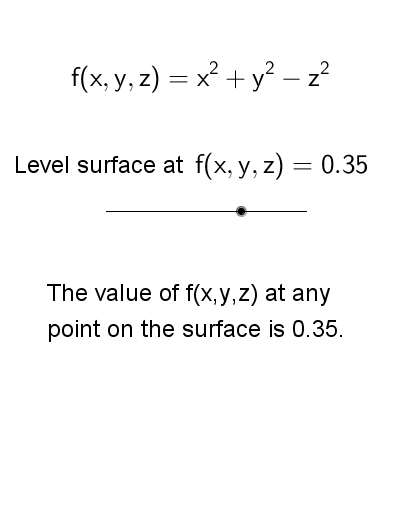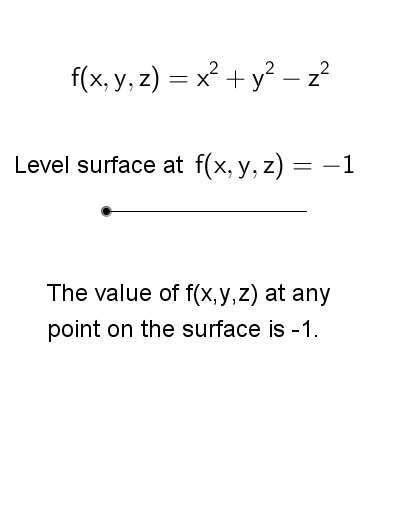
Scroll down to the bottom to view the interactive graph.

Level surface are basically the same as level curves in principle, except that the domain of \(f(x,y,z)\) is in 3D-space. Therefore, the set \(f(x,y,z) = k\) describes a surface in 3D-space rather than a curve in 2D-space.

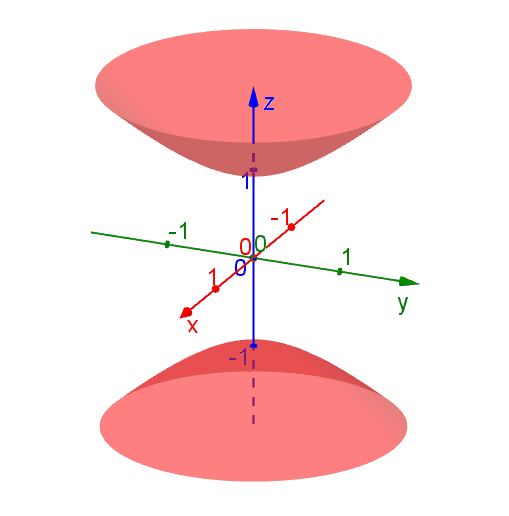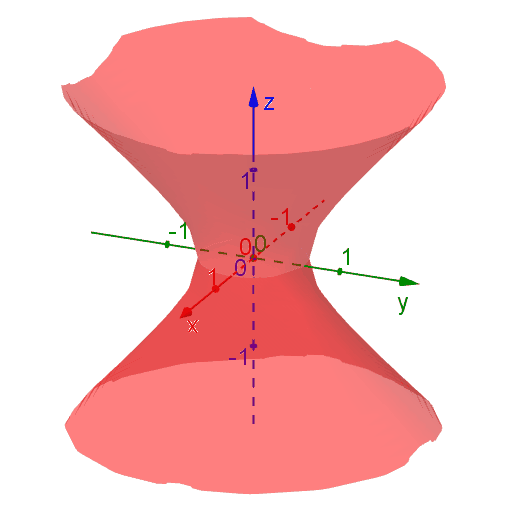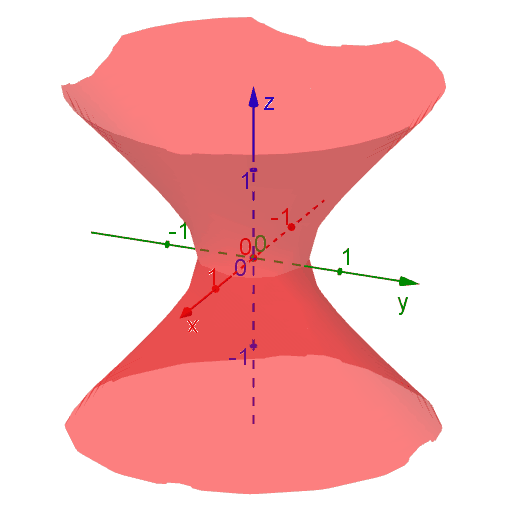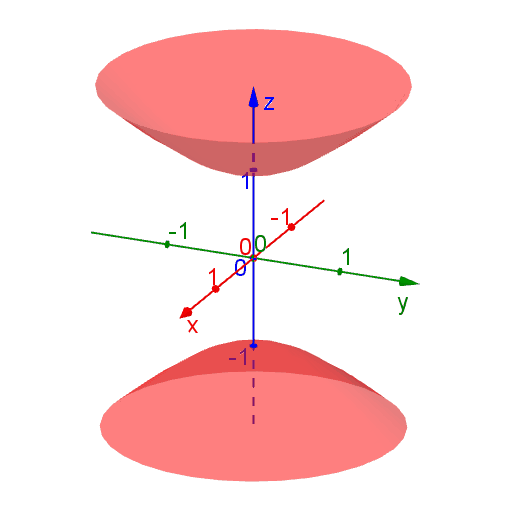
The following diagram shows the level surfaces \[f(x,y,z) = x^2 + y^2 - x^2 = k\] for various \(k\) values. The level surfaces are hyperbolas of one or two sheets, depending on the values of \(k\). Nevertheless, the value of \(f(x,y,z)\) stays the same at each points on a level surface.

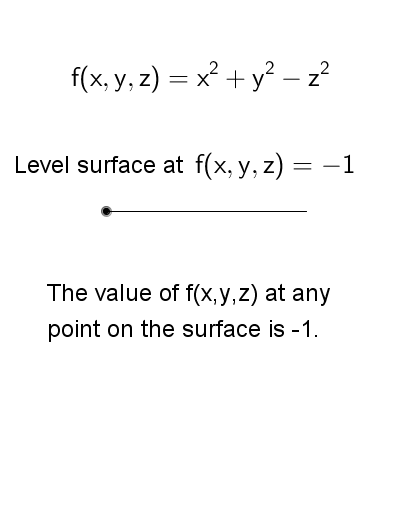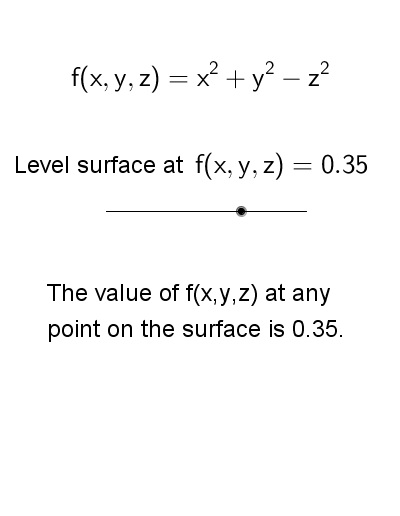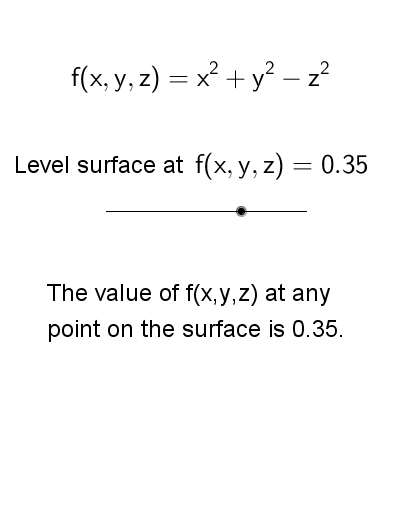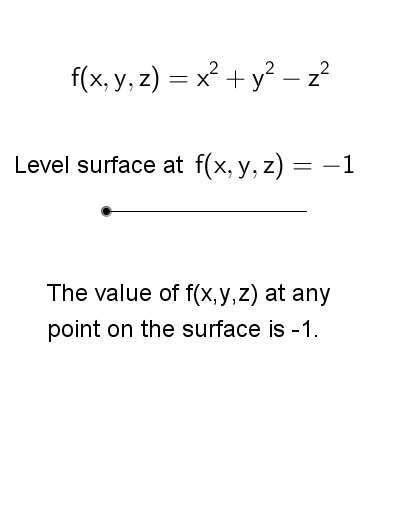
To view the interactive graph:

1. Make sure you have the latest version of Java 7 installed in your computer. Tablets and smartphones are not supported.
2. Download this file, levelsurface.ggb.
3. Click here to open GeoGebra.
4. After you open GeoGebra, click "File" in the toolbar, then click "Open".
5. Choose the .ggb file you just downloaded and click the "Open" button.
6. Now you should be able to view the graph inside GeoGebra.

To rotate the graph, right click and drag.

Joseph Lo