Scroll down to the bottom to view the interactive graph.
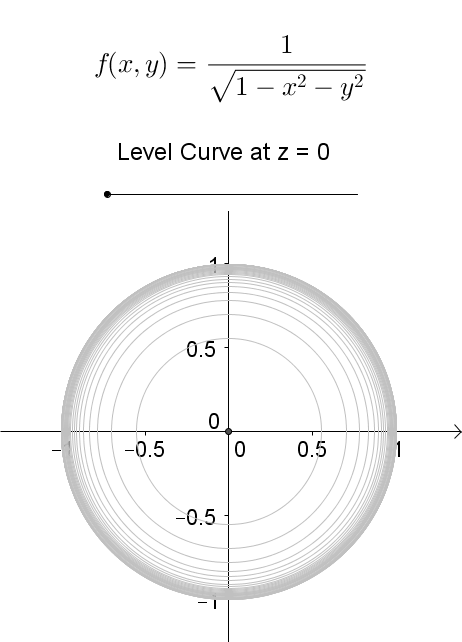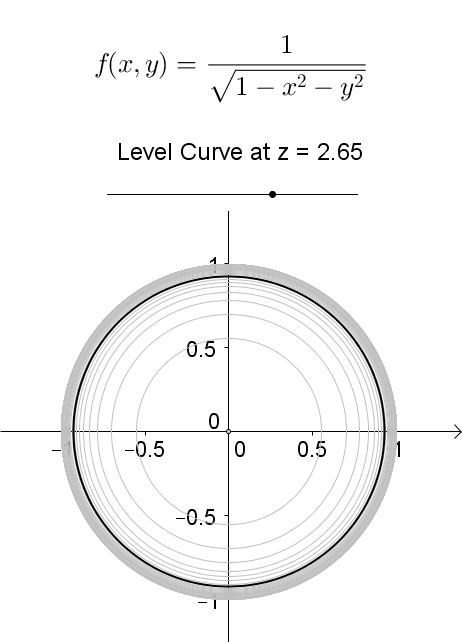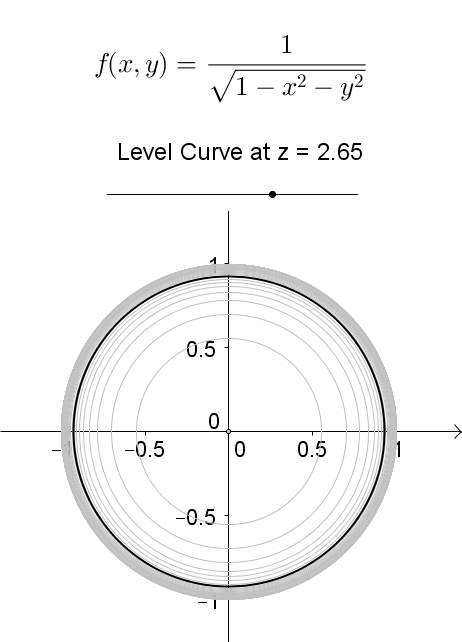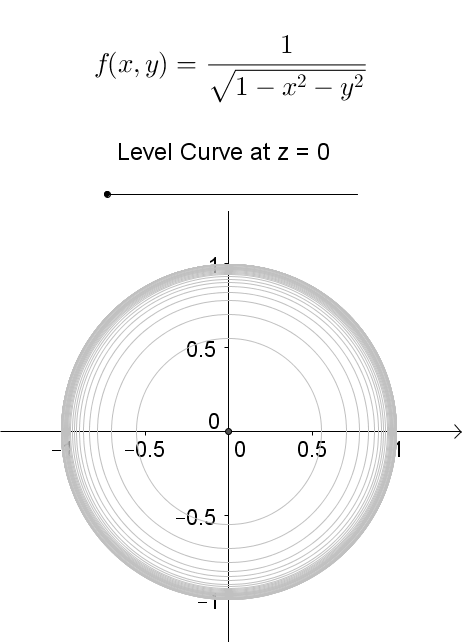
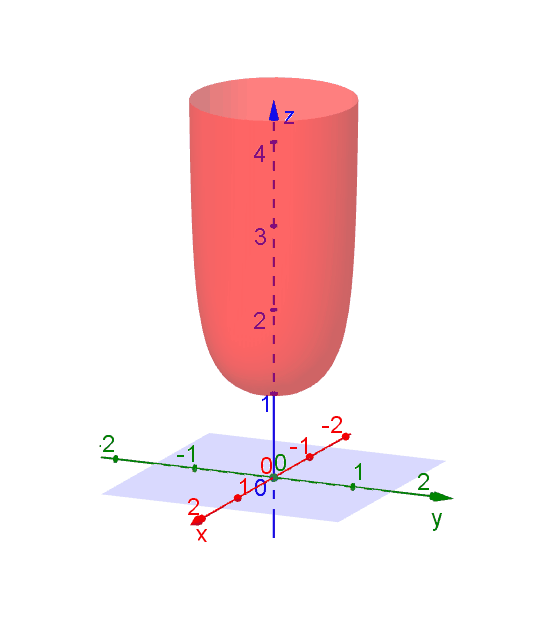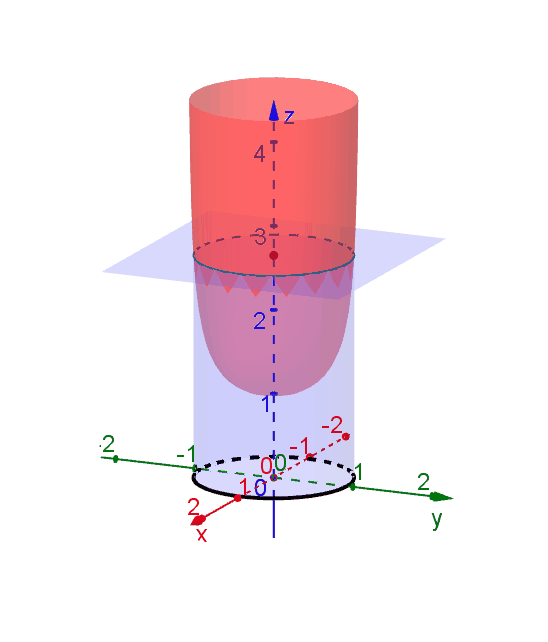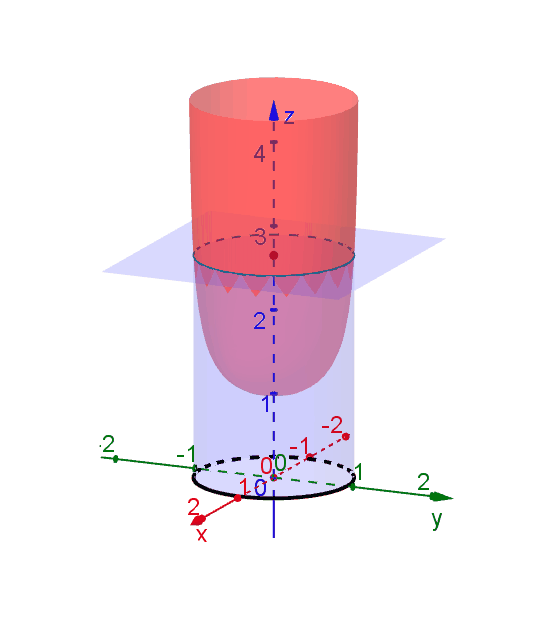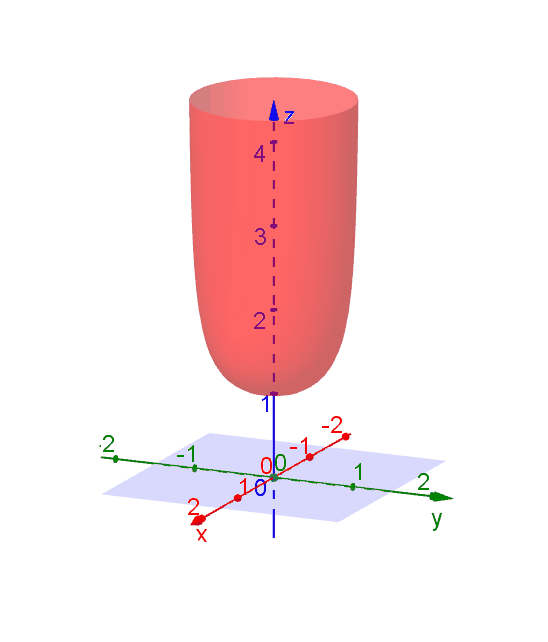
A level curve of \(f(x,y)\) is a curve on the domain that satisfies \(f(x,y) = k\). It can be viewed as the intersection of the surface \(z = f(x,y)\) and the horizontal plane \(z = k\) projected onto the domain. The following diagrams shows how the level curves \[f(x,y) = \dfrac{1}{\sqrt{1-x^2-y^2}} = k\] changes as \(k\) changes. Note that the level curves are circles given by \[x^2 + y^2 = 1-\dfrac{1}{k^2}\] for \(k \ge 1\), for which the radii never exceed 1. For \(k < 1\), the plane \(z = k\) does not intersect with the surface and hence there are no level curves.


To view the interactive graph:
To rotate the graph, right click and drag.
Joseph Lo