Hyperbolic paraboloid

Scroll down to the bottom to view the interactive graph.

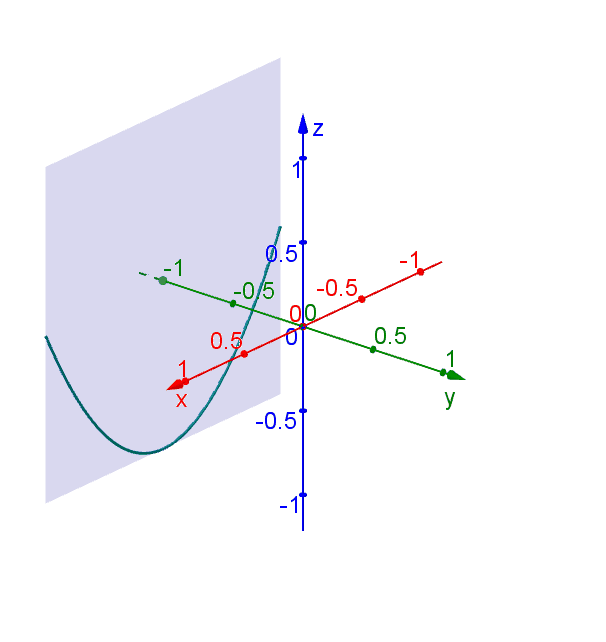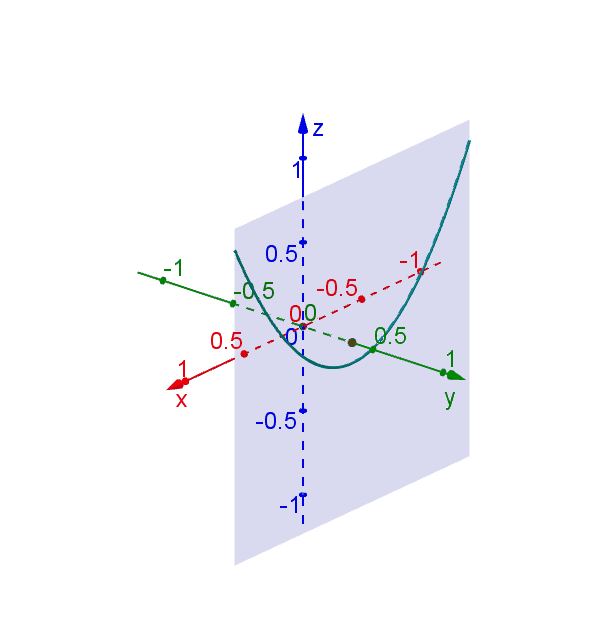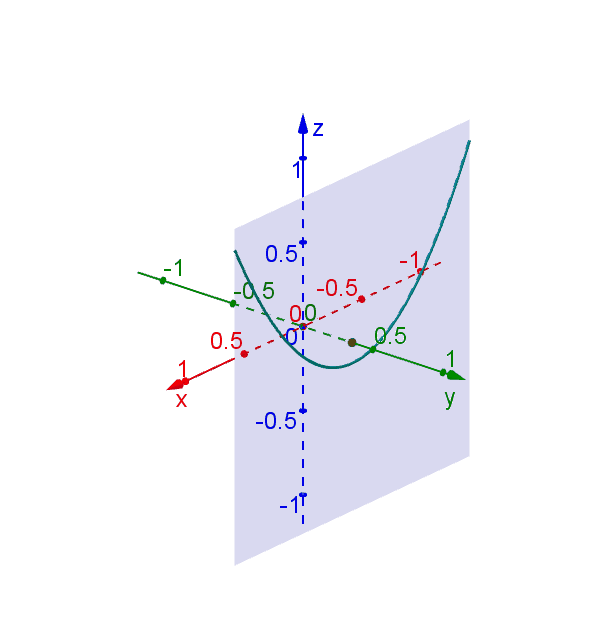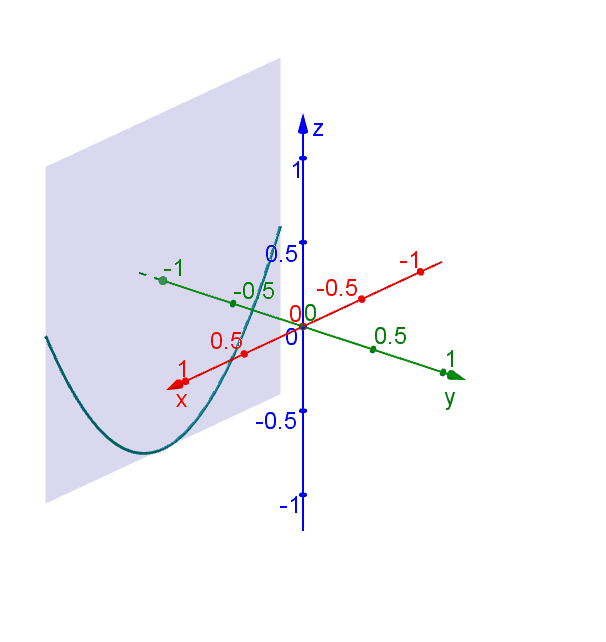
Consider the function \[f(x,y) = x^2 - y^2.\] To illustrate the surface \(z = f(x,y)\), we can try to imagine how the traces look like when fixing \(x\) or \(y\). For example, if we fix \(y\), i.e. set \[y = k = \text{constant,}\] then the trace along the surface is defined by \(z = f(x,k) = x^2 -k^2\), which is a parabola opening upward and shifted down by \(k^2\).

The shape of the surface will be apparent if we put all the traces together.

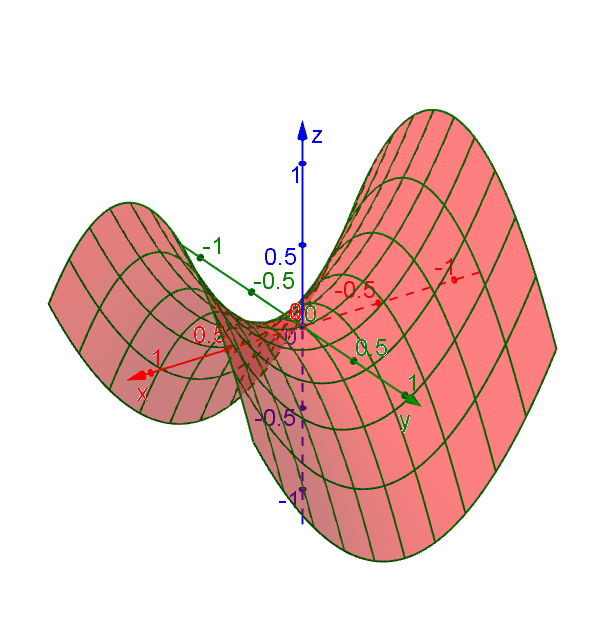
You may see this in 3D if you have a pair of red-cyan 3D glasses.

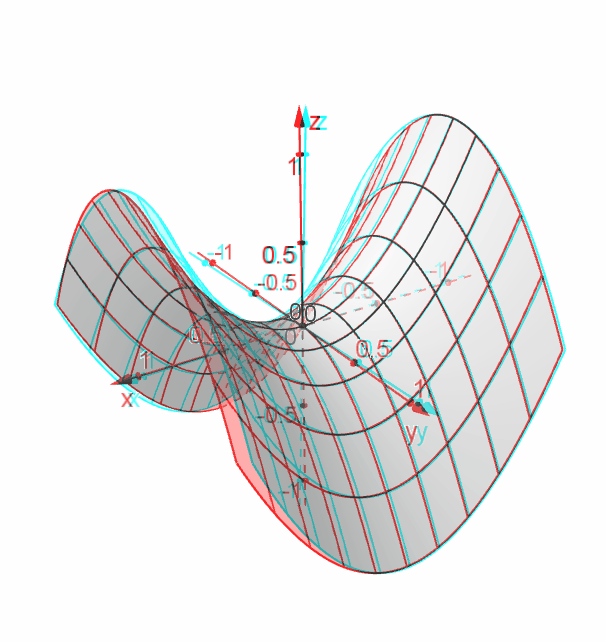
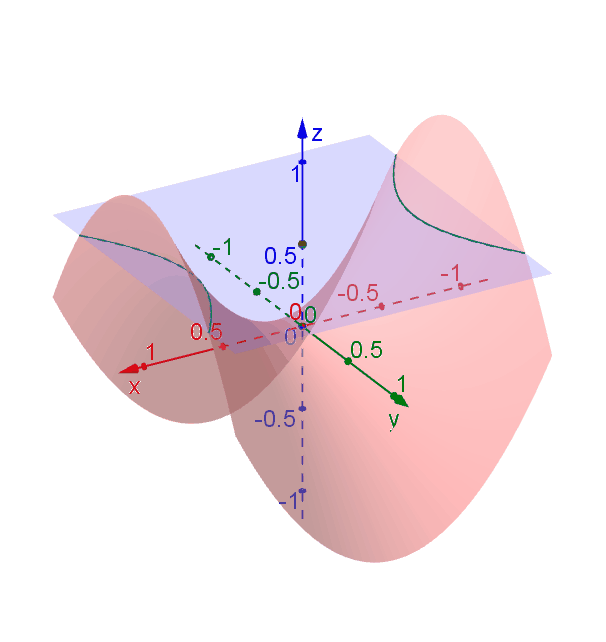
This surface is called a hyperbolic paraboloid because the traces parallel to the \(xz\)- and \(yz\)-planes are parabolas and the level curves (traces parallel to the \(xy\)-plane) are hyperbolas. The following figure shows the hyperbolic shape of a level curve.

To view the interactive graph:

1. Make sure you have the latest version of Java 7 installed in your computer. Tablets and smartphones are not supported.
2. Download this file, hyperbolic_paraboloid.ggb.
3. Click here to open GeoGebra.
4. After you open GeoGebra, click "File" in the toolbar, then click "Open".
5. Choose the .ggb file you just downloaded and click the "Open" button.
6. Now you should be able to view the graph inside GeoGebra.

To rotate the graph, right click and drag.

Joseph Lo