
Scroll down to the bottom to view the interactive graph.
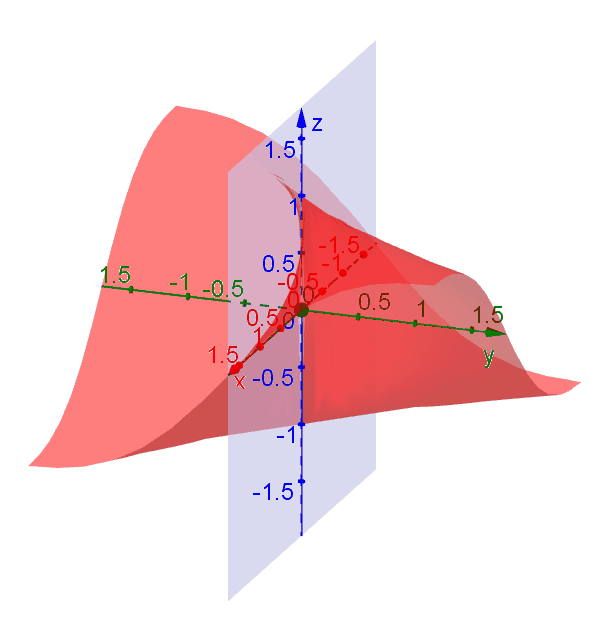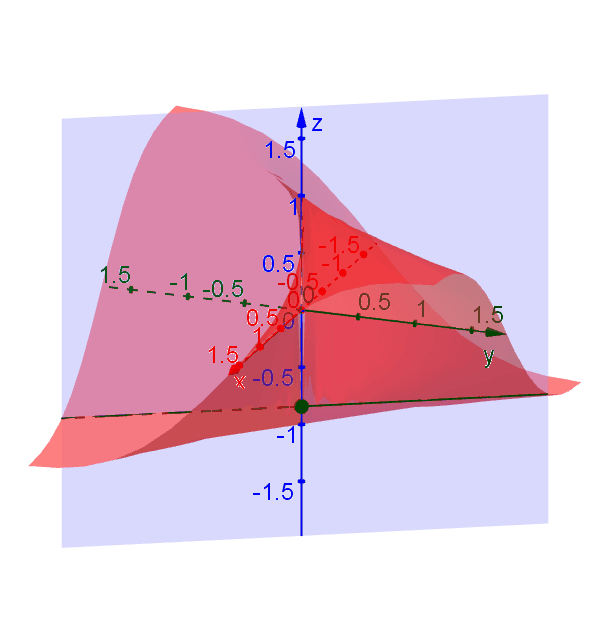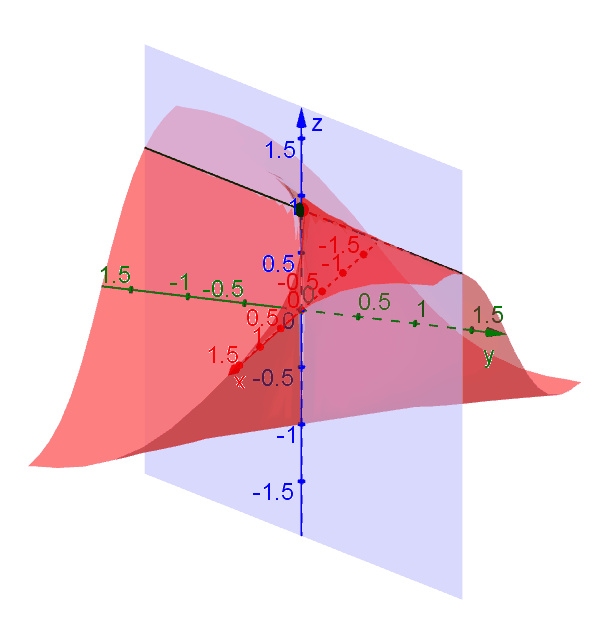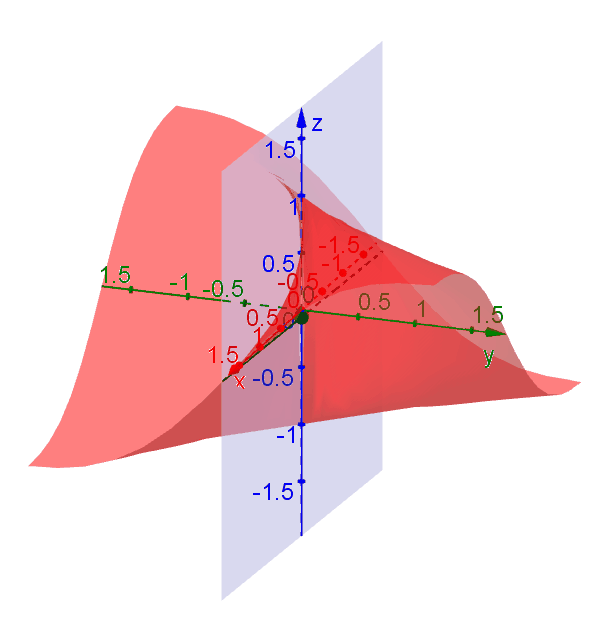
A function \(f(x,y)\) is continuous at a point \((x_0,y_0)\) if \[\lim\limits_{(x,y)\to(x_0,y_0)} f(x,y) = f(x_0,y_0).\] For example, the function \[f(x,y) = \dfrac{2xy}{x^2+y^2},\] is discontinuous at \((0,0)\) because \(f(0,0)\) is not defined. If we look more closely, however, we will notice that the function does not have a limit at \((0,0)\) either, but we could indeed find a limit no matter with direction we choose to approach to \((0,0)\).
Suppose we approach \((0,0)\) along the direction which makes an angle \(\theta\) with the \(x\)-axis. In this case the trajectory can be described by \((x,y) = (t\cos\theta, t\sin\theta)\) when \(t \to 0\). Plugging it in \(f\) gives \[f(t\cos\theta, t\sin\theta) = \dfrac{2t^2\cos\theta \sin\theta}{t^2\cos^2\theta + t^2\sin^2\theta} = \sin 2\theta.\] As \(t\to 0\), \(f \to \sin 2\theta\) which depends on \(\theta\). Since \(f\) approaches to different values along different trajectories, we say that the limit \(\lim\limits_{(x,y)\to(0,0)} f(x,y)\) does not exist.


To view the interactive graph:
To rotate the graph, right click and drag.
Joseph Lo