
Scroll down to the bottom to view the interactive graph.
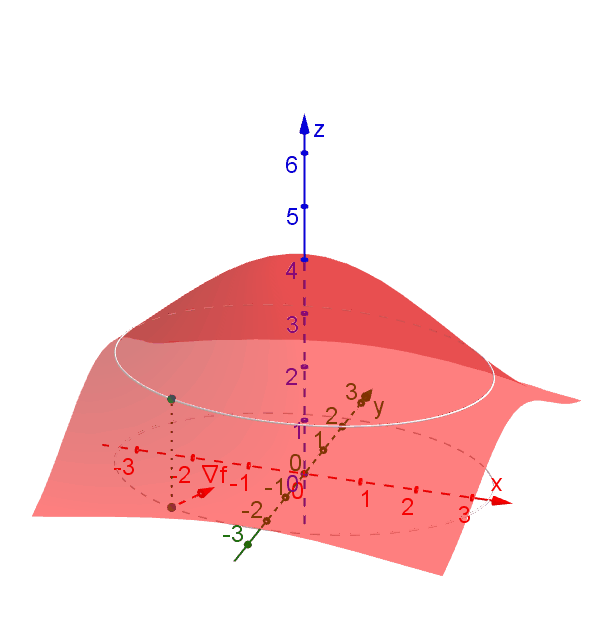
The directional derivative of a function \(f(x,y)\) at a point \(P_0 (x_0,y_0)\) in the direction \(\textbf{u} = \left\langle a,b \right\rangle\), denoted by \[D_{\textbf{u}} f(x_0,y_0),\] is recognized as the slope of the line tangent to the surface \(z = f(x,y)\) at \(P_0\) in the direction \(\textbf{u}\) on the domain.
As long as \(f\) is differentiable at \(P_0\), we can use the tangent plane to come up with a simple formula \(D_{\textbf{u}} f = \textbf{u} \cdot \left\langle f_x,f_y \right\rangle.\) This directional derivative is at its maximum value if \(\textbf{u}\) points to the direction \(\nabla f = \left\langle f_x,f_y \right\rangle\).
If \(\textbf{u}\) points to the direction tangent to a level curve, then we must have \(D_{\textbf{u}} f = 0\). This also holds when \(\textbf{u} \perp \nabla f\). As a result, the vector \(\nabla f\) points to the direction perpendicular to a level curve.


The sign of \(D_{\textbf{u}} f\) can be determined based on the angle \(\theta\) between \(\textbf{u}\) and \(\nabla f\). The derivative \(D_{\textbf{u}} f\) is positive if \(\theta \in [0,\pi/2)\) and is negative if \(\theta \in (\pi/2,\pi]\).


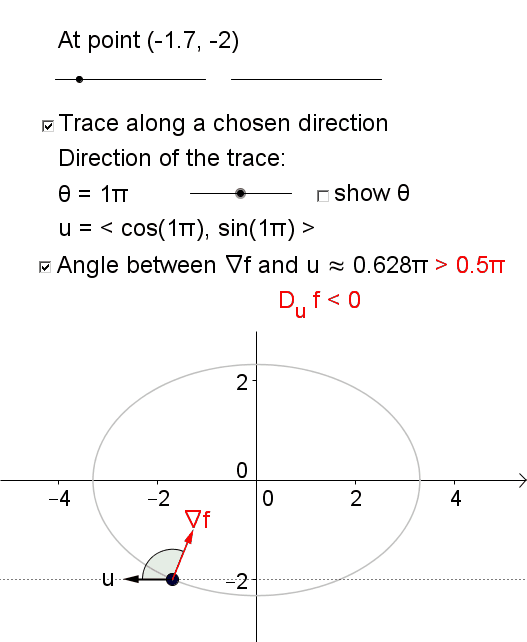
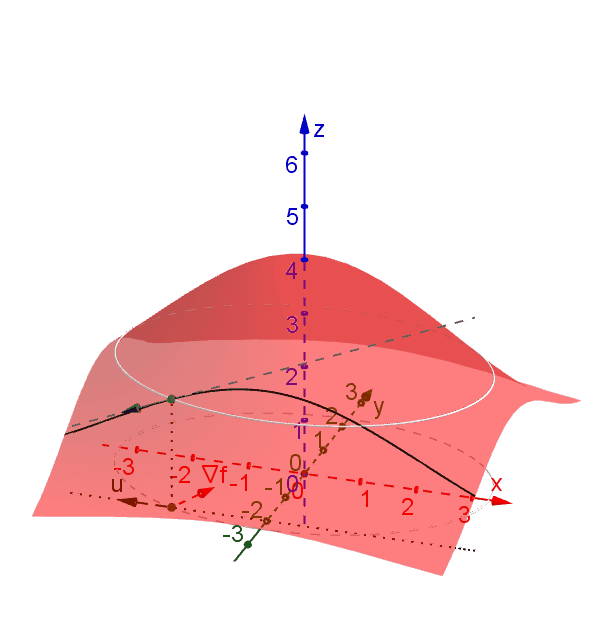
To view the interactive graph:
To rotate the graph, right click and drag.
Joseph Lo