Critical Points of a differentiable function

Scroll down to the bottom to view the interactive graph.

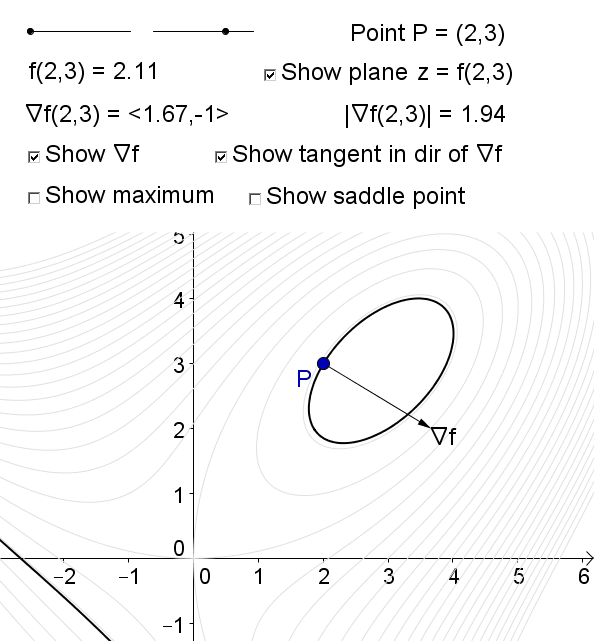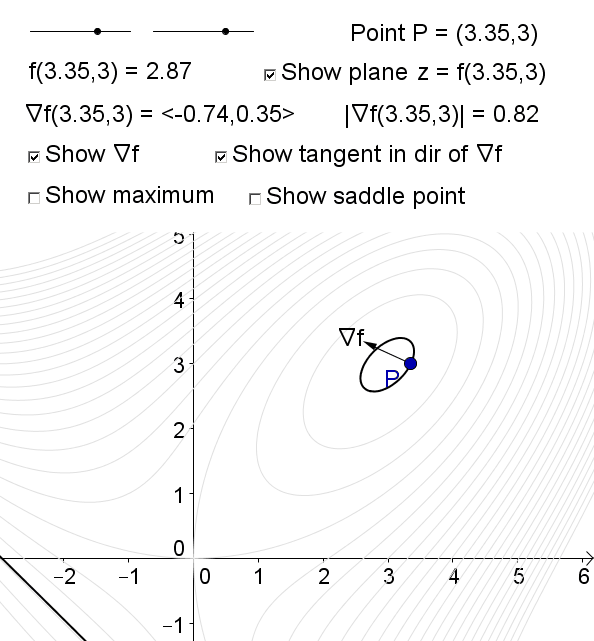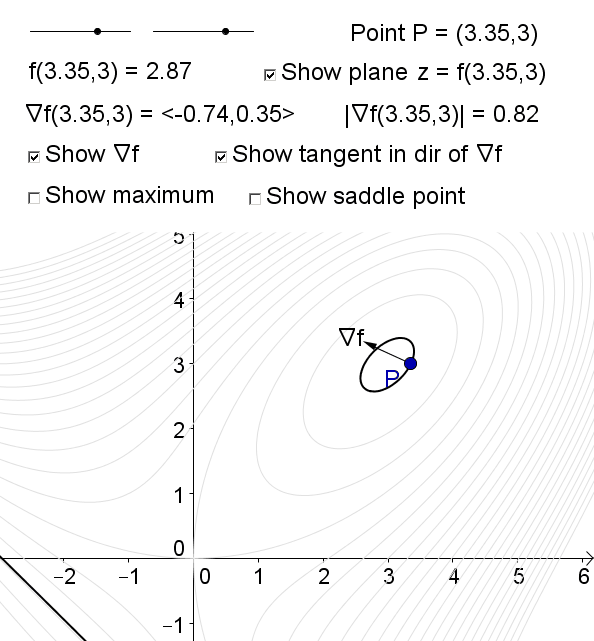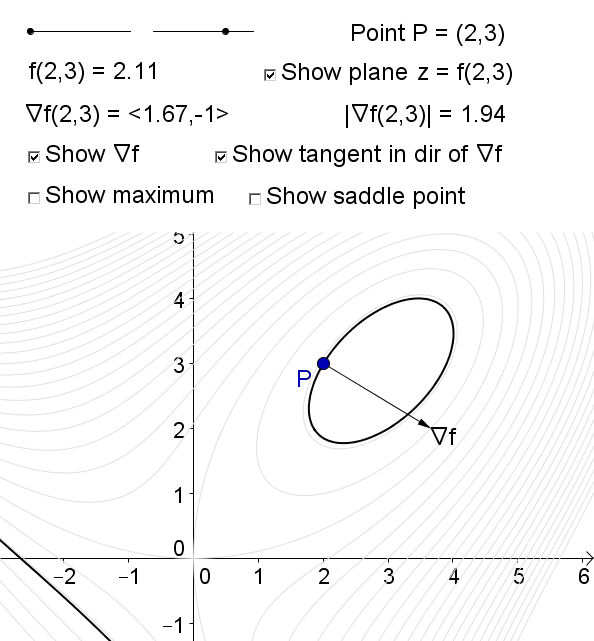
Consider the function \[f(x,y) = xy - \dfrac{1}{9} (x^3+y^3).\] The critical points (\((0,0)\) and \((3,3)\)) occur when \(\nabla f = \langle f_x, f_y \rangle = \langle 0, 0 \rangle\). There are no other critical points since \(f(x,y)\) is differentiable for all \(x\) and \(y\).

The diagram shows the surface of \(f(x,y)\) and its level curve containing the point \(P(x,y)\). As \(P\) approach the critical points, \(\nabla f \to \langle 0,0 \rangle\)

To view the interactive graph:

1. Make sure you have the latest version of Java 7 installed in your computer. Tablets and smartphones are not supported.
2. Download this file, criticalpoints.ggb.
3. Click here to open GeoGebra.
4. After you open GeoGebra, click "File" in the toolbar, then click "Open".
5. Choose the .ggb file you just downloaded and click the "Open" button.
6. Now you should be able to view the graph inside GeoGebra.

To rotate the graph, right click and drag.

Joseph Lo