|
The first interesting combinatorial result was found by Jacques Tits.
In principle, in showing that one word in S is
equivalent to another,
it could be necessary to inflate the sizes
of words as well as shrink them. Tits showed
around 1968 that no inflation was necessary.
Although this result will play no very practical role, the
result is useful in hand calculation,
and I will present here a slight modification of Tits' proof.
Changing Tit's terminology slightly, I define
reduction of a word in S
to be the process of iterating these two transformations of words:
- deleting a pair s # s;
- replacing one side of a braid relation by the other.
Here I use # to denote concatenation of words.
Let R(w) be the set of all words obtained by all reductions of w.
It is a finite set, although in general quite large.
It includes, for example, all reduced expressions for the element
represented by the word, which for even small groups can be huge.
The longest element of
H4, for example (a group of 14,400 elements whose longest
element has length 60) has, Du Cloux tells me,
1,852,659,333,124,308 reduced expressions!
At any rate, the number of such expressions for a long element can
be reasonably expected to be huge.
There are three properties of reductions that
are straightforward:
- If y lies in R(x) then R(y) is contained in R(x);
- if y lies in R(x) and l(x) = l(y) then R(y) = R(x);
- R(s # x) contains s # R(x).
Here, l(x) is
the length of x as a word, not as an element of W.
The third property is a special case of the more general fact
that reduction is context-free: that R(x # y # z) contains
x # R(y) # z.
Theorem 1. (Jacques Tits) In order for two words x and y to
be equivalent, it is necessary and sufficient that their reduction sets R(x)
and R(y) have an element in common.
Proof. If the intersection
is non-empty,
then certainly the two
are equivalent.
The non-trivial half of the Theorem
is to show that if x and y are equivalent
then R(x) and R(y) intersect.
We may assume that
l(y)  l(x).
Now, the points (i, j) with j l(x).
Now, the points (i, j) with j  i
look like this in the plane: i
look like this in the plane:

In particular, as the illustration shows,
there is a natural order in which to count such points,
and the proof proceeds by induction on
the index of the pair l(x), l(y).
If l(x) = 0 the assertion is trivial.
Suppose now that l(x) > 0, that l(y)  l(x).
Our induction assumption is that
the Theorem is true for all pairs x*, y* with
l(x*) < l(x) or l(x*) = l(x) but l(y*) < l(y). l(x).
Our induction assumption is that
the Theorem is true for all pairs x*, y* with
l(x*) < l(x) or l(x*) = l(x) but l(y*) < l(y).
Suppose that there exists z with l(z) < l(x) lying in R(x).
Of course z and y are equivalent.
If l(y) < l(x) than (z, y) < (y, x) since l(y) < l(x).
If l(y) = l(x) then (z, y) < (y, x) since l(y) = l(x)
but l(z) < l(y). Either way, we deduce by induction
that R(z) and R(x) overlap,
hence R(x) and R(y) as well.
So we may assume from now on that
- all elements of R(x) have the same length as x.
Since l(x) > 0, x = s # x* for some s.
If R(x*) contains elements of length less than that of x*,
then since R(x) contains s # R(x*) so does R(x)
contain elements of length less than that of x,
a contradiction. So we know that
- all elements of R(x*) have the same length as x*,
which is l(x) - 1.
Suppose that y = s # y*.
Then x*, y* satisfy the induction
hypothesis, so that R(x*) and R(y*) have an element in common.
But then so do s # R(x*), s # R(y*), hence R(x) and R(y).
So now we may assume that
- y = t # y* with t different from s.
In these circumstances, l(y) must be the same
as l(x).
For suppose that l(y) < l(x).
The elements s # y and x*
are equivalent. Therefore by the induction assumption
R(s # y) and R(x*) have a common element.
But since all elements in R(x*) have the same length,
l(s # y) = l(x*) = l(x) - 1. And R(s # y) = R(x*).
Therefore s # s  y lies in R(x),
and y lies in R(x). This contradicts our current assumptions. y lies in R(x),
and y lies in R(x). This contradicts our current assumptions.
So now we may assume (a) l(y) = l(x),
and (b) x = s # x*, y = t # y*, with s and t distinct.
Since x and y are equivalent, as elements in W they satisfy
sx < x, tx < x, sy < y, ty < y.
Therefore they are longest in
their common Ws, t-coset.
Hence there exists a distinguished z in Ws, t with x, y equivalent to
ss, t z, where sz > z, tz > z, ss, t the longest element
in Ws, t. Then y* is equivalent to s # t ... z,
x* is equivalent to t # s ... z, and by induction
R(y*) = R(s # t ... z),
R(x*) = R(t # s ... z), and
R(x) = R(s # x*) = R(s # t  s ... z),
R(y) = R(t # y*) = R(t # s s ... z),
R(y) = R(t # y*) = R(t # s  t ... z).
But the last two are equivalent according to the braid relation,
hence R(x) = R(y). QED t ... z).
But the last two are equivalent according to the braid relation,
hence R(x) = R(y). QED
Because of the potentially huge size of R(x), it is definitely not usually
practical to calculate it. Nonetheless, Tits' reductions are
easy enough to carry out by hand in simple cases,
and his Theorem assures that this effort will not be fruitless.
Also, in principle Tits' algorithm tells us
how to calculate products. For this,
choose an ordering of the elements of S
(or, equivalently, index S). Assign to
each element in W its unique
ShortLex word. Calculating the product
of two words x and y means finding the ShortLex expression
of the concatenation z of the words. We can do this
by calculating R(z) and listing in order in order all
those words in it of shortest length. There are standard
computer algorithms to do all these operations
fairly efficiently,
given the essential inefficiency
of the process itself.
Exercise 2.
(A minor research problem) Turn this proof
into an algorithm that starts with a chain
of relations allowing either insertions or deletions
and winds up with a pair of reductions.
|
|
I believe, for reasons that will be laid out
later on, that regular expressions will prove to be unavoidable
in understanding important phenomena associated to Coxeter groups.
How important remains to be seen. Nonetheless, for this reason
it seems useful to look at them in more detail. There are many
points that haven't been touched upon yet, and a few that haven't
been made very precise.
I should also point out that by no means
all
interesting languages are regular. The simplest example
is that of balanced left and right parenthetical
expressions. The point is that
a regular language has only a limited memory, whereas
whether or not a parenthesis `)' is balanced somewhere in an expression
by a `(' may involve searching back to the beginning
of the expression.
Deterministic automata
The following are examples of how one normally writes
positive rational numbers:
13, 2/4, 20/47, 1/24.
These are not:
13/1, 02/4, 0/0 .
Note that we are not restricting ourselves to reduced fractions.
We can put together
a recipe for expressing a positive rational number:
(1) To write a positive integer we
write a sequence of non-negative digits, starting
with a positive one.
(2) To write a positive rational number,
write a positive integer,
followed optionally by a slash /
followed by a positive integer other than 1.
This recipe is not trivial to read, and for most
people it is easier to understand if we
encode it in a diagram:
This looks like a finite automaton, but there is a
new feature - the red nodes. The point is
that not all paths in this diagram lead to
an acceptable expression for a fraction. The prefix of a valid expression
for a fraction may not be itself valid.
For example, the empty string is not acceptable.
Also, a single 1 in the denominator is not acceptable.
In this diagram, only those paths leading to
a yellow node correspond to acceptable
expressions.
The yellow nodes are said to be the accepting states
of the automaton.
So we have a precise definition:
a deterministic automaton is a directed graph together with
an alphabet (also called the set of imput symbols).
The edges in the graph are labeled by symbols
from the alphabet, and there is at most
one edge with a given label leaving any node.
Some of the nodes are designated as accepting states
and one of them as the start state. To such a graph
is associated a language in the alphabet S, namely
those words accepted by a path in the automaton.
A path is a sequence of node n0, n1, ... , nm
and it accepts the word s1 ... sm if (a) n0 is the start
state; (b) nm is an accepting state;
(c) there is an edge from nk-1 to nk labeled by sk.
If the graph is finite,
the language is called regular.
This is a crucial restriction, since for any language
we can make a recognizing automaton from the tree of all
words in the language, which I call the tautologous
automaton of the language.
Exercise 4.
Design a finite automaton that represents real numbers.
Why can't we expect a finite automaton to recognize reduced fractions?
Whether an expression is recognized by a finite automaton depends on
its form, not its content - its syntax, not its semantics.
Deciding whether a fraction is reduced or not involves
thinking about the meaning of fractions, not just their form.
We shouldn't expect anything as simple
as a finite automaton to handle this sort of thing. Syntactical
analysis is often, however, a preliminary to semantic interpretation.
Non-deterministic automata
There are also non-deterministic automata.
Or, more properly, not-necessarily-deterministic automata.
I abbreviate the term as NDA.
There are three modifications: (1) There may be several starting
states; (2) there may be unlabeled edges; (3) there may
be several edges with a given label leaving a node.
If s1 ... sm is a word in the alphabet, a path accepting this string
is a sequence of nodes n0, n1, ... , nm in the automaton
such that (a) n0 is one of the start states;
(b) nm is one of the accepting states;
(c) from nk-1 to nk there is a directed sequence of edges,
one labeled by sk and the rest unlabeled. What is new is that the path
is not determined by the word; there may
be several paths all accepting the same word.
Such diagrams are technically very useful,
but do not actually enlarge the meaning
of the term `regular expression'.
Equivalent automata are those that recognize the same words in
the same alphabet.
Proposition 2.
Every finite NDA is equivalent to a finite deterministic one.
Proof.
Suppose given an automaton A.
How is an equivalent deterministic one constructed? First of all,
nodes in the new automaton are going to be
defined as certain subsets of nodes in the original,
which I'll call A. And there are two simple auxiliary constructions
to be applied in the course of the construction.
(a) If X is any set of nodes in A,
define its saturation S(X) to be the union of X
and all nodes reachable from X by an unlabeled edge.
A set is called saturated if it is its own saturation.
(b) If X is a saturated set of nodes in A and s an input
symbol, define X # s to be the saturation of
the set of nodes which are the target of
an edge labeled by s leading from a node in X.
It is entirely possible that X # s = X # t for distinct s
and t.
The nodes of the new automaton are the saturated subsets of
the nodes of A. There is an edge labeled by s from X
to X # s. The start state is the saturation of the set of start
states of A. A node is accepting if it contains an accepting node from
A. I leave it as an exercise to verify that this equivlent to A.
The new automaton may be huge. In practice, most of the
new nodes may be thrown away, because they are not
attainable from the start state. As an extreme example, if
A is itself deterministic then the only attainable nodes are
the singletons. The standard algorithm for constructing
the new automaton constructs only those new nodes
which are attainable.
The potential exponential growth does occasionally happen.
Construction of the deterministic automaton
Irredundant automata
A node in an automaton is called redundant if no path
from a start state reaches it. Eliminating these produces
an equivalent automaton.
Dead states
An automaton is called complete if
for each node n and each input symbol s there exists
an edge from n labeled by s.
Any automaton A can be converted easily into an equivalent complete
one by adding to it a dead state.
This new node is not accepting, and all edges from it lead to itself.
If n is a node of A without an edge from it labeled by s,
then in the new automaton there will be an edge labeled by s
leading to the dead state.
Inversion
The usefulness of non-deterministic automata becomes clear when
one tries to build an automaton recognizing the same strings as
an automaton A, but read backwards. We simply define a new automaton
to have as its nodes the same nodes of A.
Its starting states are the accepting states of A, the single
accepting state of the new automaton is the start state of A,
and edges in the new automaton are reversed from those of A.
That is to say, to an edge from x to y in the original
corresponds an edge from y to x in the new one, with
the same label.
This is a very simple construction, but almost always the new automaton will be
non-deterministic. Thus:
Proposition 3. The inverted words of a regular language also
form a regular language.
This accounts for the result that InverseShortLex is a regular language if ShortLex is.
Concatenation
If X and Y are languages, then the concatenation of
the two is the set of all words x # y constructed by concatenating
a word x from X with on from Y. It is denoted X # Y.
Proposition 4.
The concatenation of two regular languages is again regular.
Proof. Let X and Y be the two languages,
A and B recognizing automata.
We want to construct an automaton
recognizing X # Y in simple terms from A and B.
An example will motivate the construction,
which might otherwise seem mysterious.
Suppose X is the language containing just the words
a and ab, while Y is that containing just
b and bc. Then X # Y is made up
of ab, abb, abc, abbc. The minimal deterministic
automata for these three languages are
The problem is that there is no way to see how the automata for
X and Y are related to that for X # Y. The source
of the difficulty is that the b in abb
is different from that in abc - one comes from X and
the other from Y. There is apparently no
direct way to build a deterministic automaton directly from
the two components, but there is nonetheless a
simple solution: instead of trying to build a deterministic
automaton recognizing X # Y we shall build a non-deterministic one.
The dual source of the letter b will be dealt with
(at least implicitly) by allowing two edges from
a given source labeled by b. The actual construction for an arbitrary
X and Y is this:
Make up a new version of A by adding to a copy of it
a new terminal node z, with
unlabeled transitions to it from
each accepting state in A. Now add on to this in turn
a copy of B, with unlabeled transitions from z
to any of the starting states of B (only one, of
course, if B happens to be
deterministic). The accepting nodes of the
new automaton are just the accepting states of B.
Repetition
If X is a languages, then the repetition of X is
the language of all words obtained by concatenating
0 or more words from X.
It is denoted X*.
Proposition 5.
The repetition of a regular language is again regular.
Proof. Suppose A recognizes X.
Add two nodes to a copy of A, at the beginning
and end. From the first add unlabeled edges to
all start states of A, and from each of the accepting states
add an unlabeled edge to the last.
From the last back to the first also
add an unlabeled edge.
Make each of the new nodes
accepting, as well as those of A.
Add the first to the start states.
Alternation
If X and Y are languages, then the alternation of
the two is the set of all words w which lie in either X or
Y.
It is denoted X | Y.
Proposition 6.
The alternation of two regular languages is again regular.
Proof. Suppose X, Y, A, B as above.
Make up a new automaton by starting
with copies of A and B. Add in a single new node,
with unlabeled edges leading from it to
all start states of either A or B. Make it the single
start state of the new automaton.
Negation
If X is a regular language,
then the words in the same alphabet which are not in E
also make up a regular language. This new language is
called the negation of the original language X
and is denoted !X.
Keep in mind that this negation is with respect to
the given alphabet.
Proposition 7. The negation of a regular language is regular.
Proof.
Suppose that A
is a complete automaton recognizing X.
The recognizing automaton for its negation
has the same nodes, edges, and start state as A, but its
accepting states are the complement of the accepting states
in A.
Intersection
If X and Y are languages, then the intersection of
the two is the set of all words simultaeously in
both languages.
It is denoted X & Y.
Proposition 8.
The intersection of two regular languages is again regular.
Proof.
It is the negation of the alternation of their negations.
Minimal automata
Any language is recognized by a unique smallest automaton.
There is an efficient algorithm to compute the equivalent minimal
automaton from any given finite one.
Here's an example we have seen already. The tautologous automaton recognizing
reduced words for A1~ is
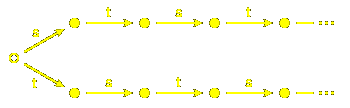
But now some of the nodes are equivalent in the sense that
the paths out of these nodes are the same - i.e. the options for continuing
a word from that node are the same. In this picture, all the nodes
coloured green are equivalent since all paths out of any of them
is just a repeated st ... , and all those coloured blue are
also equivalent:
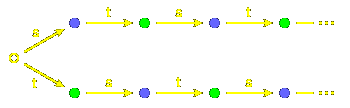
We can collapse all of the same colour to a single point, to get
a new equivalent automaton:
This construction is always valid, but a bit of care is
required. It is not the full set of words leaving a node
which is important, but just those which lead to acceptable
nodes. For example, a few extra edges could always be added to
a dead state without changing things substantially.
If A is any automaton, define two
nodes n1 and n2 to be equivalent if they have the following property:
a word w leads from n1 to
an accepting state in A
if and only if it leads from n2 to an accepting state.
Define a new automaton whose nodes are the equivalence classes of nodes in A.
It start state is the class containing the start state of A. Its accepting states
are those classes containing accepting nodes of A. There is an edge
labeled s from a class N1 to a class N2 if there is
an edge from n1 in N1 to n2 in N2 labeled by s.
I leave it as an exercise to verify that this is an equivalent deterministic automaton.
The minimization algorithm
There is an algorithm for producing the minimal
automaton equivalent to a given one which is remarkably efficient.
To explain it, I begin by putting the problem more constructively.
Let A be the given automaton, which for the moment I assume complete.
Nodes n1 and n2 of A are called equivalent if
for every word w in the alphabet of A the nodes
n1 # w and n2 # w are either both
accepting or both not. Break this down into more a more explicit
test. Divide the nodes into two blocks, the accepting nodes
and the rest. Call two nodes equivalent of order 0 if they
are both in the same block. Inductively, call node n1 and n2 equivalent
of order m+1 if they are equivalent of order m and the nodes
n1 # s and n2 # s are also equivalent of order m for all
symbols s. Thus they are equivalent if they are equivalent of
all orders.
Suppose we have already found the blocks B of elements equivalent of order m,
and suppose there are k input symbols. Then we partition each block
B into smaller blocks BC1, ... , Ck,
where BC1, ... , Ck is the set of b in B
such that b # si lies in the block Ci, for each i = 1, ... , k.
If there are N blocks of order m equivalence, then a priori there
might be as many as Nk+1 blocks of order m+1, a potentially disastrous super-exponential
growth.
In fact there exists an algorithm with time dependence
O(k n log n) if n is the number of states in the original automaton.
This works because most of the blocks BC1, ... , Ck
will be empty, so the idea is to find away of going from
one order to the next by somehow automatically excluding the empty ones.
This algorithm solves a slightly more general problem,
one which occurs when dealing with Coxeter groups.
Suppose we are given a collection of maps fi, i
varying over a set S, and a partition of a set X into
blocks Xi. Two elements x and y are called
equivalent if any iteration of the f's applied to them finds them
in the same block. We shall call an element dead if all the f's take it to
itself.
It works like this,
in a rough description:
|
Start with the partition into two blocks, accepting and non-accepting.
Maintain a list of pairs (B, s), to be processed in the order in
which they are put on the list, and start the list off by
putting all (B, s) on the list where B is the block of
accepting states and s ranges over all the input symbols.
While this list is not empty: take a pair (B, s) off the list.
For each node y in B look at all nodes x with x # s = y.
Record the block Bx in which x appears. After all y have been examined,
look at each of the blocks B* that have been met in this way. If the total
number of times they have been encountered is not equal to
the total number of elements in B*, then divide
B* into two parts, the x such that x # s lies in B#, and the rest.
Let C be the smaller of these two subsets of B*. Put (C, s)
on the process list for all input symbols s. Loop.
In implementing this, before beginning make for each y and s a list of all
nodes x with x # s = y. As we process the elements y of
a block B we maintain a list of all x we meet with x # s in B
as well as the block to which x belongs. We also maintain a list
of those Bx, but each one listed only once. After we have examinedd all
y in B, we go through the list of the B* met, comparing it to
the set of x in it. If we do create a new block
C by removing elements from B* we do one of two things: put (C, s) on the process
list if (B*, s) is on that list; or if not then we put the smaller
of (C, s) and (B*, s) on the list.
|
|
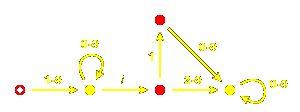
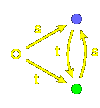
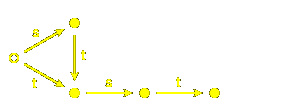
Let's look at the
ShortLex
words for a more complicated infinite Coxeter group,
that with Coxeter diagram 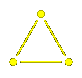 .
It is an affine group, and we shall look at it as generated by affine reflections.
There are three generators, which I write as 1, 2,
3. Each element of the group is represented by a
ShortLex word, hence a path of coloured arrows
from the chamber C to the chamber wC.
Because of uniqueness, the paths all together
make up a tree with C as its root. .
It is an affine group, and we shall look at it as generated by affine reflections.
There are three generators, which I write as 1, 2,
3. Each element of the group is represented by a
ShortLex word, hence a path of coloured arrows
from the chamber C to the chamber wC.
Because of uniqueness, the paths all together
make up a tree with C as its root.
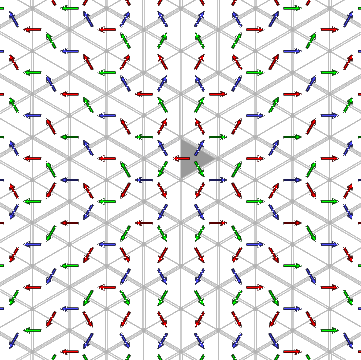
Certain things are not difficult to see in this image.
Every non-empty ShortLex expression starts with
one of the three symbols 1, 2, or
3, so the chambers other than C are partitioned
into three corresponding regions of the plane. Because of the ordering of
the three,
(1) the w starting with
1 are those chambers on the side of
the line of reflection a1 = 0 opposite to C;
(2) those w starting with
2 are those chambers on the side of
the line of reflection a2 = 0 opposite to C,
but not already in the first region;
(3) those starting with 3 are those
chambers on the side of
the line of reflection a3 = 0 opposite to C,
but not already in either of the previous two.
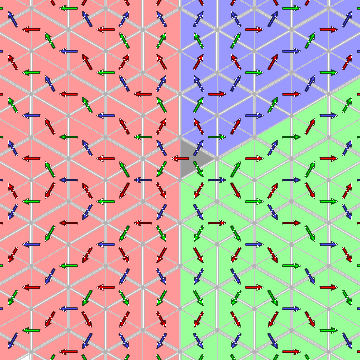
It is significant that each of these regions is convex.
Indeed, it appears that all of the regions
comprised of a single chamber together with its
successors in the tree are convex. We shall why this is
so in a moment.
The question is whether we can recognize in this tree a repetition of
patterns similar to that in the tree for A1~. The answer is that we can.
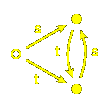
For example, there exist some simple cycles
132 ...

There are lots of such cycles - in the following picture,
each yellow chamber represents the same position in such a cycle:

But there are more interesting repetitions:
Start out at C and move by 3.
You arrive at essentially the same pattern if you follow this by
1213.
What do I mean by `the same pattern'? That the tree of paths leading out
of the two chambers are congruent. If you pick up
one of these trees, so to speak, and shift
it rigidly to the other chamber, you can then lay it down upon the
tree leading out of the second. (Of course I am not claiming to
prove this, but all evidence is in favour of the assertion.)
There are other chambers equivalent to these two, too.
All such positions are shown here:

Two chambers will be called ShortLex congruent
if the pattern of transitions in the ShortLex tree
out of each of them is the same. If this happens,
then there exists an element of the Weyl group
transforming one of these patterns onto the other.
It turns out for A2~ as for A1~
(although we have only suggested that it is true, certainly not proven it)
that the set of all
ShortLex expressions for this group is a regular language,
or in other words that there are a finite number of congruence classes.
Here is the corresponding finite automaton:
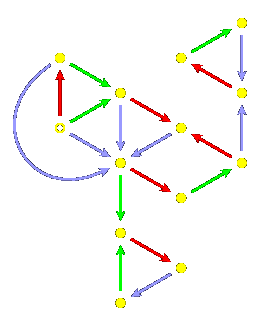
Note that there are indeed loops
132
and
1213,
as well as
123.
This is not an isolated case. It is a very beautiful result of
Brigitte Brink and Bob Howlett that:
Theorem 9. For any
Coxeter group, there are finite automata recognizing
ShortLex expressions, InverseShortLex expressions, and reduced words
in the group.
We shall look at the proof in subsequent sections.
That InverseShortLex is a regular language follows formally
from the regularity of ShortLex,
since it is just the reversed language.
It is reasonable to think of both of
these as lacking in significance,
perhaps to be considered results in applied rather than pure
mathematics. But that reduced words should also
be recognized by a finite automaton must be
a fundamental property of Coxeter groups.
For finite and affine groups it is not a very deep result;
it is equivalent to other more familiar properties
of these groups. But for other groups
it is not at all a trivial fact, and that it has taken so long to
be discovered is likely just a sign that not much
work has been devoted to these groups.
Here is the finite automaton recognizing reduced words for A2~:
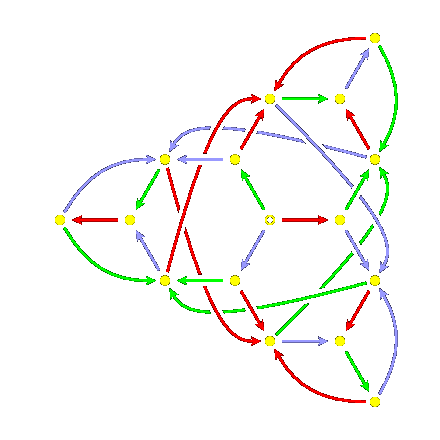
Its symmetry arises from the symmetry of the Coxeter diagram.
Embedded in it are three hexagons, which are the finite automata
for the dihedral
groups of two generators, each of order 6. The minimal finite
automaton recognizing reduced words for a finite
Coxeter group is always the same size
as the group itself - this is essentially because all
words terminate in the longest element.
Exercise 5.
Prove this last assertion - that any finite automaton recognizing
the reduced expressions for a finite Coxeter group
have to have size at least that of the group itself.
|
The key to the proof of the Theorem of Brink and Howlett
is a more fundamental result of theirs
about the roots of a Cartan realization of a Coxeter group.
One positive root b is said to dominate another positive root
a if the two roots are distinct and the intersection of the half-space a > 0
with the Tits cone  is entirely contained
in the half-space b > 0. In other words, if whenever
wC lies in the region a > 0 then it also lies in the region b > 0,
equivalently if whenever
w-1a > 0 then w-1b > 0 also.
I call a root minimal
if it does not dominate any roots. (This notion was first
applied seriously by Bob Howlett and Brigitte
Brink. Their terminology differs from mine -
In their joint paper they use
the term elementary, and Howlett still prefers this.
In a subsequent paper Brink uses the term
dominance minimal, to take account of the distinction
between the partial ordering on roots determined by dominance
and another one to be introduced later on.) For finite groups,
the Tits cone is all of V,
so there is no dominance and all positive roots are minimal. For affine groups
the concept is also simple. In this case the positive roots are of the form
a + c for all positive roots a of
the associated finite root system and non-negative
integer constants c, as well as -a + c where a is positive and c is
a positive integer. Thus whenever one root dominates another the
root hyperplanes must be parallel.
The basic ones are the basic roots of the finite system
together with -a + 1, where a is what is common
called the dominant root (although there is no relation
with the dominance defined here).
The minimal roots are those of the form a or -a + 1
where a is positive in the finite system. But for other groups
the concept is more subtle. Here is what happens for
the group with Coxeter diagram is entirely contained
in the half-space b > 0. In other words, if whenever
wC lies in the region a > 0 then it also lies in the region b > 0,
equivalently if whenever
w-1a > 0 then w-1b > 0 also.
I call a root minimal
if it does not dominate any roots. (This notion was first
applied seriously by Bob Howlett and Brigitte
Brink. Their terminology differs from mine -
In their joint paper they use
the term elementary, and Howlett still prefers this.
In a subsequent paper Brink uses the term
dominance minimal, to take account of the distinction
between the partial ordering on roots determined by dominance
and another one to be introduced later on.) For finite groups,
the Tits cone is all of V,
so there is no dominance and all positive roots are minimal. For affine groups
the concept is also simple. In this case the positive roots are of the form
a + c for all positive roots a of
the associated finite root system and non-negative
integer constants c, as well as -a + c where a is positive and c is
a positive integer. Thus whenever one root dominates another the
root hyperplanes must be parallel.
The basic ones are the basic roots of the finite system
together with -a + 1, where a is what is common
called the dominant root (although there is no relation
with the dominance defined here).
The minimal roots are those of the form a or -a + 1
where a is positive in the finite system. But for other groups
the concept is more subtle. Here is what happens for
the group with Coxeter diagram 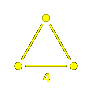 : :
In this and a few other simple cases the minimal roots all touch the chamber C,
but that does not always happen.
The fundamental result of Brink and Howlett ,
upon which all their non-trivial results depend, is that:
Theorem 10.
For any Coxeter group there are only
a finite number of minimal roots.
Bob Howlett remarks somewhere that he thinks this is
a fundamental fact about Coxeter groups,
even though there seem to be few
applications of it to other properties, and I agree
with him.
I am not going to prove the theorem of Brink and Howlett here,
but I shall explain some more elementary properties of minmal
roots.
There are two interesting order relations among positive roots.
One is dominance, which we have seen already.
The other is more closely related to
how the positive roots are generated. Every positive root
is equal to the transform of a basic root
by and element of W. Define the depth
of a root p to be the least length of a w such that w-1 p < 0.
This is also 1 less than the least length of
a w such that w-1 p is a basic root.
Geometrically, it is the length of the least gallery
starting at C with terminal
chamber in the region p < 0.
Thus the depth of a basic root is 1.
Define p  q if q = w p,
where the depth of q is equal to the sum
of the depth of p and the length of w.
We thus have a labeled directed graph: there is
an edge from p to q labeled by s in S
if d(q) = d(p) + 1 and s p = q, and p q if q = w p,
where the depth of q is equal to the sum
of the depth of p and the length of w.
We thus have a labeled directed graph: there is
an edge from p to q labeled by s in S
if d(q) = d(p) + 1 and s p = q, and p  q if
there exists a sequence of edges in this root graph
from p to q. q if
there exists a sequence of edges in this root graph
from p to q.
1. The minimal roots are minimal in this order.
2. If p is a minimal root and s in S,
then exactly one of these holds:
(a) p = as, and s p < 0;
(b) s p is another minimal root;
(c) s p dominates as.
Thus we get the minimal root
reflection table.
In cases (a) we write s p = -, in case (c)
we write s p = +, else s p = q.
The minimal root reflection table is an important tool
in algorithms involving Coxeter groups.
The root hyperplanes p = 0 and q = 0 intersect in
 if and only if the group generated
by sp and sq is contained in
the conjugate of some finite dihedral
group Ws, t. The product st will thus be of order
dividing ms, t. if and only if the group generated
by sp and sq is contained in
the conjugate of some finite dihedral
group Ws, t. The product st will thus be of order
dividing ms, t.
Lemma. If p dominates q and wq is
a positive root then wp is also a positive root
and wp dominates wq.
If p  q and p is minimal then so is q.
If p dominates q then thedepth
of p is greater than or equal to to that of q. q and p is minimal then so is q.
If p dominates q then thedepth
of p is greater than or equal to to that of q.
Brink's thesis.
Coxeter distance.
Different definitions of depth.
Structure of the root graph?
|



 y
y





 .
It is an affine group, and we shall look at it as generated by affine reflections.
There are three generators, which I write as 1, 2,
3. Each element of the group is represented by a
ShortLex word, hence a path of coloured arrows
from the chamber
.
It is an affine group, and we shall look at it as generated by affine reflections.
There are three generators, which I write as 1, 2,
3. Each element of the group is represented by a
ShortLex word, hence a path of coloured arrows
from the chamber 





