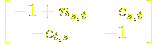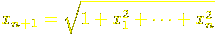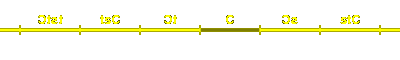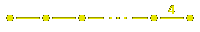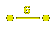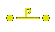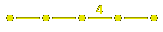|
[ Main page | Part II. Word processing | Part III. Multiplication | Part IV. Closures ] |
Coxeter groups
Part I. Geometry and combinatorics
by Bill Casselman
|
If $S@ is any set, a
$m_{t,s} = m_{s,t} > 1@ for distinct $s@ and $t@. There are naturally occurring cases where $S@ is infinite, but in these notes $S@ will be assumed to be finite. We shall see eventually that this is not a serious restriction.
Associated to a Coxeter matrix is a
For example, if the Coxeter matrix is
The
This simple definition conveys, without elaboration, no idea of how interesting such groups are. They are among the most intriguing of all mathematical structures. |
More precisely, the definition sets $W@ to be the set of
words in $S@ (i.e. finite sequences $s_{1} ... s_{n}@ of elements of $S@)
modulo an equivalence relation.
Words $x@ and $y@
are equivalent if $x@ is obtained from $y@ by a chain of these
elementary transformations:
$stssts=stts@, $stts=ss@, $ss=1@.
If a Coxeter diagram decomposes into two components
$S_{1}@ and $S_{2}@, then the corresponding group
is a direct product of the groups
parametrized by $S_{1}@ and $S_{2}@.
All words in an equivalence class have the same parity - either even or odd.
The
A word is said to be
If $T@ is a subset of $S@, then the inclusion of $T@
in $S@ induces a canonical map from $W_{T}@ to $W_{S}@.
It is not clear a priori that this
is an embedding, although it will turn out that this is so,
or that a shortest expression of an element
in the image by elements of $T@ will also be one by elements of $S@.
For the moment, all we can see easily is that
|
|
It is possible to develop the subject of Coxeter groups entirely
in combinatorial terms (this is done - well, at least thoroughly attempted - in
the book by Bourbaki), but certain geometric representations
of Coxeter groups, in which the group acts discretely
on a certain domain, and in which the generators are
represented by reflections, allow one to visualize nicely
what is going on.
Recall that a
There are other kinds of reflections, too, but they reduce to
linear ones. They are discussed at the end of this section.
The hyperplane fixed by the reflection is where $a = 0@, and $a^{v}@ is mapped to its negative as long as $< a , a^{v} > = 2@. The function $a@ and vector $a^{v}@ are unique up to non-zero scalar multiples. If $a@ is replaced by $ca@ then $a^{v}@ is replaced by $c^{-1}a^{v}@.
Often a reflection will be orthogonal with respect to
some inner product
In this situation, the dot product induces
a linear map from $V@ to the linear dual space $V^{*}@, and $a@ is the image of
$2 a^{v} / (a^{v}
The group $GL(V)@ acts by its definition on $V@,
and on $V^{*}@ according to
the prescription $< ga, gv > = < a, v >@.
(If vectors are column vectors, then linear functions are row vectors
and the canonical pairing is the matrix product $a v@.
If $g@ is represented by the matrix $M@ then $g@ takes
$v@ to $Mv@ and $a@ to $a M^{-1}@.)
At any rate, the group $GL(V)@ acts transitively on pairs $(a, a^{v})@,
hence all reflections are conjugate to each other.
Let $s@ and $t@ be a pair of reflections, say corresponding to
$a, a^{v}@ and $b, b^{v}@.
Define associated real constants
Let $(s_{1}, t_{1})@ and $(s_{2}, t_{2})@ be pairs of reflections, conjugate
under the linear transformation $g@. Then
for some non-zero constants $c_{a}@ and $c_{b}@, and
consequently $c_{s2, t2} = (c_{b}/c_{a}) c_{s1, t1}@,
$c_{t2, s2} = (c_{a}/c_{b}) c_{t1, s1}@.
The constants $c_{s, t}@ and $c_{t, s}@ are therefore not
conjugation-invariant,
but the product $n_{s,t} = c_{s, t}c_{t, s}@ is.
For generic pairs it will turn out to possess a simple interpretation.
One way to understand conjugation-invariant phenomena
is to consider geometrical configurations - for example,
how the various hyperplanes and lines relate qualititatively to each other.
One possibility is that in which
the reflection hyperplanes of $s@ and $t@ are the same.
In this case we may take $a = b@. Then
We are especially interested in the case where $n_{s, t} = 4@ but
$a@ and $b@ are linearly independent.
If $L@ is the intersection of the kernels of
$a@ and $b@, then $s@ and $t@ induce reflections
on the two-dimensional quotient $V / L@. In this plane
$a^{v}@ and $b^{v}@ are linearly dependent. We have
$c_{s, t}c_{t, s} = < a, b^{v} > < b, a^{v} > = 4@,
and we can scale $a@ so that in fact
$c_{s, t} = c_{t, s}@, both being equal to
$2@ or $-2@. In either case, $a^{v}@ and $b^{v}@ lie on a single line through
the origin, and both $s@ and $t@ transform a vector $v@ in a direction parallel to that line.
In particular the products $st@ and $ts@ are shears along that line.
The region on one side of that line and in between the two lines
$a=0@ and $b=0@ will be a fundamental domain for the group acting
on the corresponding open half-plane.
If we choose the signs of $a@ and $b@ correctly we may assume that
this region is that where $a > 0@ and $b > 0@. In that case, with our normalization,
$c_{s , t} = c_{t, s} = -2@.
From now on, suppose that $n_{s, t}@ is not equal to $4@.
Then the vectors $a^{v}@ and $b^{v}@ span a plane transversal
to the intersection of the kernels of $a@ and $b@, and in effect we
may restrict ourselves to dimension $2@. In these circumstances,
reflections fix lines.
There is one other exceptional collection of cases
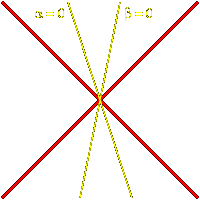
to deal with - when $n_{s, t} = 0@. This happens only when either
$c_{s, t} = < a, b^{v} > = 0@ or $c_{t, s} = < b, a^{v} > = 0@. If both are equal to
$0@, then $s@ and $t@ are a commuting pair of reflections whose product
amounts to multiplication by $-1@. The group generated by $s@ and $t@
has four elements, and any one of the four quadrants is a fundamental
domain.
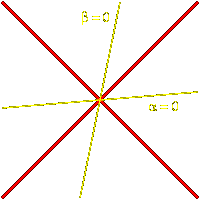
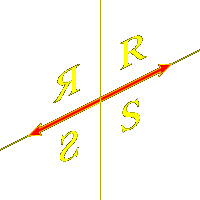
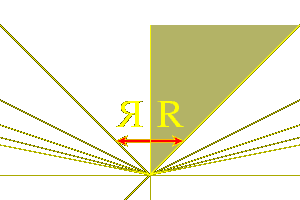
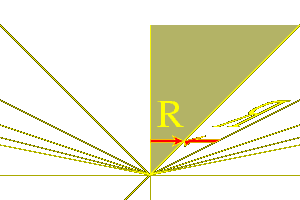
Otherwise, suppose that $< a, b^{v} > = 0@,
but $< b, a^{v} >@ is not equal to $0@.
We may arrange that $< b, a^{v} >@
is in fact positive.
Then the line $a = 0@ is fixed by both $s@ and $t@.
The reflection $s@ interchanges the two sides of this line, but $t@
preserves it.
The pair of reflections $t@ and $sts@
now both stabilize each side of the line $a = 0@, and the $n@-invariant
of this pair is $4@, since they share the eigenvector $b^{v}@.
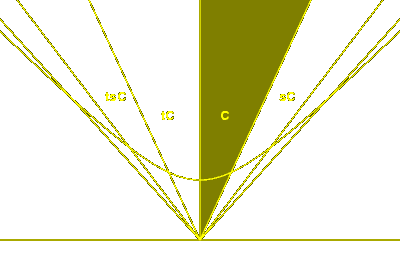
Therefore from what have already learned in this case,
we know that with a suitable choice of sign for $b@
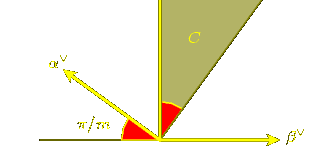
the region $C@ where $b > 0@ and $sb > 0@ on the side
of the line where $a > 0@ is a fundamental domain
for the group generated by $t@ and $sts@. Furthermore,
the reflection $s@ takes $C@ to $-C@. Note also
that the vector $a^{v}@ lies in its interior, as shown in the figure.
Later on we shall need a simple consequence of this
clear picture of how the pair $s@ and $t@ act:
in this case the region where $a > 0@, $b > 0@ is not
a fundamental domain for the group generated by $s@
and $t@. Or, in other words, if $n_{s, t} = 0@ and this region is
a fundamental domain then $s@ and $t@ are
a commuting pair of reflections, and $c_{s, t}@ and $c_{t, s}@ both vanish.
From now on, we assume $n_{s, t}@ to be neither $0@ nor $4@.
As one consequence, $-2 + n_{s,t}@ is the trace of $st@,
hence clearly conjugation-invariant.
Since $n_{s, t}@ is not $0@, neither $c_{s, t}@ nor $c_{t, s}@ vanish.
Therefore the single number $a^{v}
The matrix of the quadratic form is
In order for the form to be definite, it is necessary
and sufficient that $c_{s, t}@ and $c_{t, s}@ have
the same sign, and that the determinant be positive.
Therefore we must have $0 < n_{s, t} < 4@.
The picture accompanying the last assertion is this:
Suppose now that $n@ is not $4@, and that
$s@ and $t@ generate an infinite group.
We want again to see when the region $a > 0@, $b > 0@ is
a fundamental domain. From one of the Propositions just proven,
we must have $n > 4@ or $n < 0@.
In summary:
In the last two cases, $c_{s, t}@ and $c_{t, s}@ are both negative.
for some linear function $a@ and constant $c@. The linear function $a@
is the
An affine reflection is a special case of a linear one, through
the familiar trick of embedding an affine space of dimension
$n@ into a vector space of dimension $n+1@. Thus $v@ in $V@
maps to $(v, 1)@ in a larger space $V_{#}@.
Let $
The non-Euclidean space $H_{n}@ of $n@ dimension is the component
$Q(x) = x_{n+1}^{2} - x_{1}^{2} - ... - x_{n}^{2} = 1@, $x_{n+1} > 0@ of
the hyperbolic sphere,
which can be parametrized by Euclidean space $E_{n}@ according to the formula
It is taken into
itself by the connected component of the orthogonal group of $Q@
and there is a unique Riemannian metric on it invariant
under this group and restricting to the Euclidean metric
at $(0, 0, ... , 0, 1)@. There are two models of this
in Euclidean space of $n@ dimensions,
the familiar Poincaré model and the slightly less familiar Klein model.
(There is also, for $n=2@, the upper half-plane, but that is another
story.)
Both models identify $H@ with the interior of the unit ball
in $E_{n}@ centred at the origin.
For the Klein model, this ball
is identified with the intersection of the slice
$x_{n+1} = 1@ of the region $Q(x) > 0@
(the interior of a homogeneous cone). A point $x@ on $H@ maps to
$x_{*} = x/x_{n+1}@. It happens that a non-Euclidean geodesic line
between two points $x@ and $y@ is the intersection with
$H@ of the plane through the origin
containing $x@ and $y@, and this intersects the slice in a line
between $x_{*}@ and $y_{*}@. Thus in the Klein model.
points of $H@ are identified with points of the interior
of a unit ball, and geodesics between such points are line segments in the ball.
The Poincaré model is a transformation of the Klein model.
A point $x@ in the interior of the unit ball in $E_{n}@
maps to the point above it on the upper hemisphere in $E_{n+1}@,
then by South pole stereographic projection back onto the equator.
In this transformation, geodesics become arcs of circles
perpendicular to the boundary of the unit ball.
The point for us is that non-Euclidean reflections
are those induced on the hyperbolic
sphere, or either of its models, by linear reflections in $E_{n+1}@.
For both models, we start with a hyperplane $a = 0@ which intersects the
region $Q(x) > 0@ and a vector $a^{v}@ transverse to it. In the Klein model,
we take a point $x@ in the slice $Q(x) > 0@, $x_{n+1} = 1@ to
$x - < a, x > a^{v}@ and then project it back onto the slice.
We have seen examples of this also in the discussion above of pairs
of linear reflections with $n > 4@.
In the Poincaré model we unravel by stereographic projection, reflect, and ravel again.
|
|
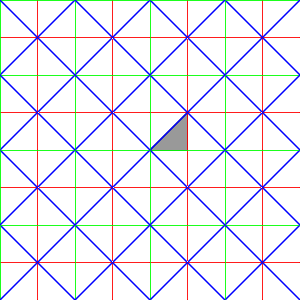
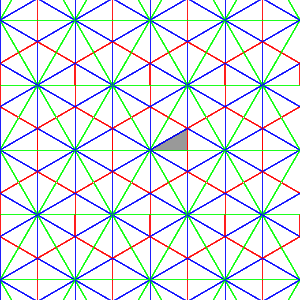
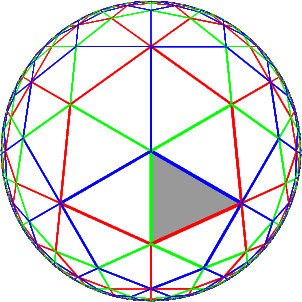
In this section we shall look at some Coxeter groups defined geometrically.
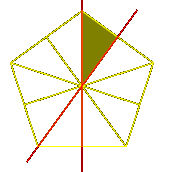
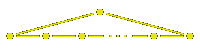
Rotations are not its only symmetries, since any line through the center of any of its sides and the origin, or any of its corners and the origin, is an axis of mirror symmetry. Since any symmetry must take a corner into some other corner, and can either preserve or reverse orientation, there are $2m@ symmetries altogether, in which the rotations form a subgroup of order $2@.
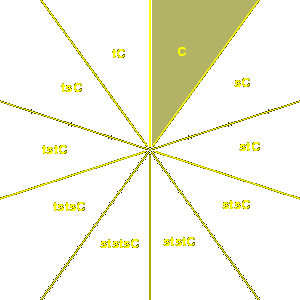
This should be clear from the picture. The generators $s@ and $t@
should be chosen to be reflections in neighbouring axes of symmetry,
as the red lines in the figure.
They are orthogonal reflections, with the angle between their
lines of reflection equal to $
The $2m@ elements of the group can be expressed as
We can see how these elements match up with transforms of $C@ in this
picture:
It is an infinite Coxeter group with two generators, say $s@ and $t@,
and with $m_{s, t}@ infinite.
As we have already seen, the realization by affine reflections
is the restriction to a line of
a linear Coxeter group in dimension $2@.
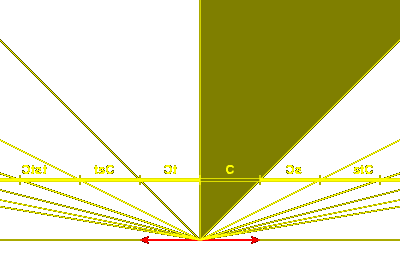
Again, if $a@ and $b@ are chosen correctly, the region where
$a > 0@ and $b > 0@ is a fundamental domain for the group.
The elements of the group can be expressed as
In brief, the argument for this is that if $sw > w@
then $w = ts .. @, and the shortest
We know that the standard
representation preserves a metric in which
$|a_{i}|^{2} = 1@ for all $i@ and $a_{i}
Here is a table of cases of possible values of the $m_{i, j}@
in weakly increasing order:
|
|
A
Every Coxeter group possesses at least one realization, as we shall see in a moment. Geometric properties of realizations translate naturally to combinatorial properties of the group. From the geometry of the simplices neighbouring a fundamental domain, for example, you can read off the Coxeter matrix. This is because if $L@ the intersection of two walls, then the configuration in the neighbourhood of $L@ is essentially that in a realization of the group generated by the two reflections in those walls. This is a special case of a very general result proven in most generality by MacBeath around 1964.
Given a realization, make a choice for each $s@ in $S@ of a
pair $a_{s}@, $a_{s}^{v}@ defining reflection in
the wall of the fundamental domain parametrized by $s@.
The sign of each function $a_{s}@
can (and always will) be made so that $a_{s} > 0@ in the interior
of the given fundamental domain. Such a linear function $a_{s}@ is
determined up to a positive scalar multiple, and its equivalence class
under such multiplications will be called a
The
Any Cartan matrix clearly gives rise to a representation
of the associated Coxeter group. In fact:
This will be proven in the next section.
One consequence is that every Coxeter group has at least one realization, since there
exists always the
Cartan matrices with integral matrices determine
Kac-Moody Lie algebras. In this case the representation
of its Weyl group on the lattice of roots is the one associated to this Cartan matrix.
Coxeter groups which occur as the Weyl groups
of Kac-Moody algebras are called
Two Cartan matrices $C_{1}@ and $C_{2}@
will give rise to
isomorphic representations of
a Coxeter group
if and only if there exists a positive diagonal
matrix $D@ with $C_{2} = D C_{1} D^{-1}@.
In particular, those Cartan matrices giving rise to realizations equivalent to
the standard one are
Distinct classes can give rise
to realizations with very different geometric properties.
We have seen this already in the case of the infinite
dihedral group,
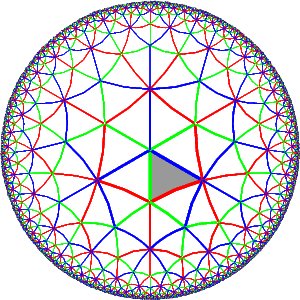
and here are the pictures for two
different realizations of the Coxeter group whose Coxeter
diagram is
The first of these is associated to the standard Cartan matrix,
and the second to the integral matrix
which is that of a certain hyperbolic Kac-Moody Lie algebra.
It is the second, therefore, which is likely to have intrinsic significance.
|
|
For the moment, fix a Cartan matrix.
It gives rise to a representation of its associated Coxeter group,
in which the elements of $s@ act by reflections.
This will be called for the moment a The principal result connecting combinatorics and the geometry of a Coxeter group is this:
This generalizes what we have already seen for groups of rank two.
The proof is somewhat intricate.
This result will be made more precise later on,
where we discuss the cosets $W_{T}\W@ in more detail.
We now prove Theorem 3 by induction on $l(w)@.
If $w = 1@ there is no problem. Suppose $l(w) > 1@.
If $x = sw < w@ it must be shown that
$a_{s}@ is negative on $wC@. But then $wC = sxC@;
by induction $a_{s}@ is positive on $xC@,
hence $sxC@ lies in the region where $a_{s} < 0@.
Now suppose $sw > 0@. It must be shown that
$a_{s} > 0@ on $wC@.
Choose $t@ such that $tw < w@. Find $u@ in
$W_{s,t}@ and $x@ in $W@ satisfying the conditions of the Lemma.
Since $tw < w@, $l(x) < l(w)@. Since $sx > x@ and $tx > x@,
induction lets us see that
$xC@ is contained in the region $C_{s,t}@ where $a_{s} > 0@ and $a_{t} > 0@.
Since $l(w) = l(u) + l(x)@, $l(su) = l(u) + 1@,
and this is still valid if $l@ is the length
in $W_{s,t}@. From the discussion on groups
of rank two, we see that $a_{s} > 0@ on
the region $uC_{s,t}@, hence on $wC = uxC@ as well.
|
|
A
The point is that the chamber $C@ is not intersected by
a root hyperplane.
This result follows immediately from Theorem 3. A reformulation:
In other words, every Cartan representation is a realization of the group
as a subgroup of $GL(V)@. If we restrict the realization to
the subgroup generated by $T@, we see that
$W_{T}@ embeds into $W@, too.
For a subset $T@ of $S@, let $C_{T}@ be the region in
the boundary of $C@ where the basic roots $a_{t} = 0@ for
$t@ in $T@, $a_{s} > 0@ for $s@ not in $T@.
Every point of $C_{T}@ is fixed by $t@ in $T@,
hence all elements of the subgroup $W_{T}@. Conversely:
In other words, each face of a chamber is labeled by
a unique subset $T@.
A
For $w@ in $W@, let
Let $R^{+}@ be the set of positive roots,
$R_{T}@ those generated by $W_{T}@ from the $a_{t}@ with $t@ in $T@.
Let $W^{T}@ be the set of these distinguished coset representatives.
These last will be left as exercises.
|
|
The chambers are parametrized by elements of $W@,
and the geometrical structure of
the complex they make up mirrors the structure of $W@.
These chambers are simplicial cones embedded in the
vector space $V@, and the left action of
$W@ on $V@ is compatible
with the left action of $W@ on itself.
But there is also a right action of $W@ on itself,
and this corresponds to a right action of $W@ on the
set of chambers. If $C_{*} = xC@ is a chamber then
$C_{*}w = xwC@ defines the right transform of $C_{*}@ by $w@.
Thus $xC = Cx@. The right action of
generators is particularly simple: $C_{*}@ and $C_{*}s@ share
a wall of codimension one labeled by $s@.
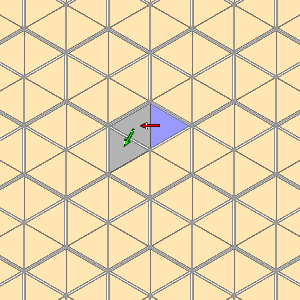
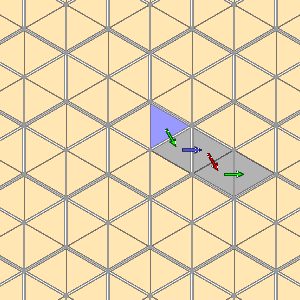
The following pictures illustrate how this works on the affine Weyl group of $A_{2}@. The chambers are really three dimensional simplicial cones, and we are looking at a slice through them, in which the generators are represented by affine reflections.
If $w = s_{1}s_{2} ... s_{n}@, then this word representation of $w@ corresponds in a simple fashion to a gallery from the fundamental chamber $C@ to $wC@ - namely, the chain of chambers $C@, $s_{1}C@, $s_{1}s_{2}C@, ... , $s_{1}s_{2} ... s_{n}C@, in that order. We read the path from left to right. |
|
Define $
It is called the
|
|
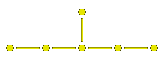
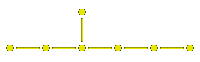
These are the Coxeter diagrams for those irreducible
Coxeter groups which are finite:
This is justified in VI.4 of the book by Bourbaki.
The basic idea is to check when the standard
realization preserves a positive definite quadratic form.
These are the cases when the Tits `cone' is the whole
vector space. The starting point is that the Coxeter diagram
cannot contain any circuits.
Another easy remark is that the number of branches
from any point can be at most $3@. But from there
the argument is complicated. The argument of Bourbaki
uses the criterion that $W@ is finite if
and only if the quadratic form
left invariant by $W@ in the standard
realization is definite. An argument along different
lines can presumably be put together
using ideas of Kac and Vinberg.
These are the Coxeter diagrams for those irreducible Coxeter groups which can be interpreted as affine reflections:
This also is in the book by Bourbaki.
These are the cases when the Tits `cone' is
a half-space.
|
|
 then its Coxeter diagram is
then its Coxeter diagram is
 .
.

 ,
,
 ,
,