More precisely, the definition sets W to be the set of
words in S (i.e. finite sequences s1 ... sn of elements of S)
modulo an equivalence relation.
Words x and y
are equivalent if x is obtained from y by a chain of these
elementary transformations:
- deleting a pair ss;
- inserting a pair ss;
- replacing one side of a braid relation by the other.
Multiplication is defined by concatenation of words.
The word 1 of length 0 is allowed, and corresponds to
the identity element.
Suppose for example that S has two elements s and t, and that ms,t = 3.
The braid relation is sts = tst. Thus (st)3 = ststst can be transformed successively to
ststst=stssts,
stssts=stts,
stts=ss,
ss=1.
Exercise 1.
Verify that if w = s1 ... sn then
w-1 = sn ... s1.
Exercise 2.
Verify that W is always a group.
Exercise 3.
Verify in general that for all s and t the product st satisfies (st)ms,t = 1.
Exercise 4.
Verify that we could have stipulated W to
be defined by relations (st)ms,t = 1.
If a Coxeter diagram decomposes into two components
S1 and S2, then the corresponding group
is a direct product of the groups
parametrized by S1 and S2.
Exercise 5.
Verify this last claim.
All words in an equivalence class have the same parity - either even or odd.
The sign of w is defined to
be 1 if its parity is even, -1 if odd. The sign
is a homomorphism from W to the multiplicative group
of 1, -1.
A word is said to be reduced if it is of minimal
length in its equivalence class. The length l(w) is
the common length of all the reduced words of w. The following is
an immediate consequence of this definition:
Proposition 1. The length has these properties:
- l(xy)
 l(x) + l(y); l(x) + l(y);
- l(w-1) = l(w);
- l(w) = 0 if and only if w is the identity;
- l(w) = 1 if and only if w lies in S (more properly, has a representative in S);
- sign(w) = (-1) l(w);
- l(ws) = l(w) + 1 or l(w) - 1;
- l(sw) = l(w) + 1 or l(w) - 1;
The last two assertions are proven by a simple parity argument.
The right weak Bruhat order on W is defined by the condition
that ws > w if l(ws) = l(w) + 1,
therefore also ws < w if l(ws) = l(w) - 1.
Similarly for the left order.
Exercise 6.
Verify this claim.
Exercise 7.
Suppose that S has two elements s and t.
Let m = ms,t .
(a) If m is finite,
verify directly from the definition that W has
2m elements, and that exactly one of them has two expressions
as reduced words.
(Hint. It is straightforward to see there are no
more than 2m elements. To see that there are exactly
that number, represent the group
by permutations of 2m elements, effectively that corresponding
to left multiplication on the group itself. )
(b) If m is infinite,
verify that every element of W has exactly one reduced expression,
and that elements of W - other than the identity - correspond bijectively to
sequences st ... and ts ... with no repetitions.
If T is a subset of S, then the inclusion of T
in S induces a canonical map from WT to WS.
It is not clear a priori that this
is an embedding, although it will turn out that this is so,
or that a shortest expression of an element
in the image by elements of T will also be one by elements of S.
For the moment, all we can see easily is that
- if w is an element of WT with image
w* in WS, then l(w*)
 l(w). l(w).
|
In this section we shall look at some Coxeter groups defined geometrically.
Finite dihedral groups
Suppose P to be a regular polygon in the plane. That is to
say, it is a polygon of m sides for some m > 2, centred at the origin,
and invariant under rotations by 2  / m. / m.
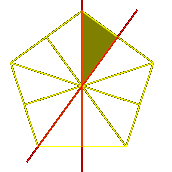
Rotations are not its only symmetries,
since any line through the center of any of its sides
and the origin, or any of its corners and the origin,
is an axis of mirror symmetry. Since any symmetry must take
a corner into some other corner, and can either preserve
or reverse orientation, there are 2m symmetries altogether,
in which the rotations form a subgroup of order 2.
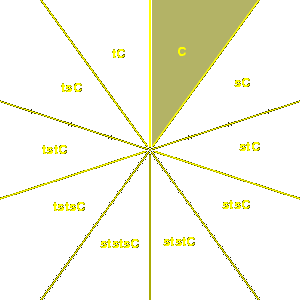
Proposition 9. The symmetry group of
a regular polygon of m sides is a Coxeter group
with two generators, say s and t. We have ms, t = m.
This should be clear from the picture. The generators s and t
should be chosen to be reflections in neighbouring axes of symmetry,
as the red lines in the figure.

They are orthogonal reflections, with the angle between their
lines of reflection equal to  /m. Choosing the signs
of av and bv correctly, we have av /m. Choosing the signs
of av and bv correctly, we have av  bv = -2 cos ( bv = -2 cos ( /m).
The region where a > 0 and b > 0 is a fundamental domain
C for the symmetry group. /m).
The region where a > 0 and b > 0 is a fundamental domain
C for the symmetry group.
The 2m elements of the group can be expressed as
1, s, t, st, ts, ... , st ... = ts ... (m terms)
We can see how these elements match up with transforms of C in this
picture:
Affine dihedral groups
Now we look at the group generated by affine reflections in the
points at the end of a line segment in one dimension.
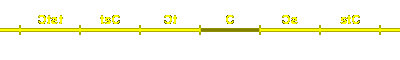
It is an infinite Coxeter group with two generators, say s and t,
and with ms, t infinite.
As we have already seen, the realization by affine reflections
is the restriction to a line of
a linear Coxeter group in dimension 2.
Again, if a and b are chosen correctly, the region where
a > 0 and b > 0 is a fundamental domain for the group.
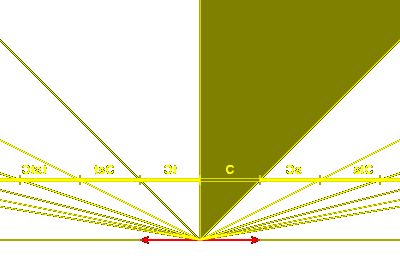
The elements of the group can be expressed as
1, s, t, st, ts, sts, tst, ...
Hyperbolic dihedral groups
Now we look at the group generated by two hyperbolic reflections
in the ends of a segment on the hyperbola Q(x, y) = 1,
where Q is an indefinite non-degenerate quadratic form.
It, too, is an infinite Coxeter group with two generators.
And again, if a and b are chosen correctly, the region where
a > 0 and b > 0 is a fundamental domain for the group.
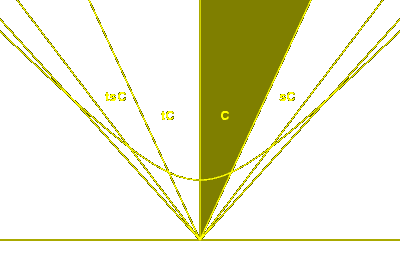
An observation about groups of rank two
The examples we have just examined exhaust the possible
representations of rank two Coxeter groups
with the property that the region C where
a > 0, b > 0 is a fundamental
domain.
An observation we shall need later, based on
observation of these cases, is that
Proposition 10. In these circumstances,
if s is a generator in S then
sw > w if and only if C and wC lie on the same side of
the line as = 0.
.
In brief, the argument for this is that if sw > w
then w = ts .. , and the shortest gallery
(sequence of contiguous chambers) from C to swC through chambers
is the reflection of the one from C to wC, except that
it starts with an extra transition from C to sC.
To be more explicit, the shortest gallery from C to wC is
the sequence
C, tC, stC, ... and is reflected into the longer
gallery C, sC, stC, stsC, ...
Groups of rank 3
Suppose now that s0, s1, and s2 generate
a Coxeter group W of rank 3 with Coxeter matrix
(mi, j) for i, j = 1, 2, 3.
I assume that all the mi, j are finite,
so that all
the dihedral groups Wi, j are finite.
How can we tell whether W is finite?
We know that the standard
representation preserves a metric in which
|ai|2 = 1 for all i and ai  aj = -cos ( aj = -cos ( /mi, j)
for i distinct from j. If we assume that
the indexing is chosen so that m1, 2 differs from 2,
then by choosing coordinates suitably (so that the finite Coxeter
group generated by the first two reflections stabilizes the (x, y)-plane)
we can arrange this metric to be x2 + y2 + c z2
with c = 1, 0, or -1, and a1 = (1, 0, 0),
a2 = (-cos /mi, j)
for i distinct from j. If we assume that
the indexing is chosen so that m1, 2 differs from 2,
then by choosing coordinates suitably (so that the finite Coxeter
group generated by the first two reflections stabilizes the (x, y)-plane)
we can arrange this metric to be x2 + y2 + c z2
with c = 1, 0, or -1, and a1 = (1, 0, 0),
a2 = (-cos  /m1,2, sin /m1,2, sin  /m1,2, 0). In order to
find a3 we have to take into account the conditions /m1,2, 0). In order to
find a3 we have to take into account the conditions
- |a3|2 = 1
- a3
 a1 = - cos a1 = - cos  /m1, 3 /m1, 3
- a3
 a2 = - cos a2 = - cos  /m2, 3 /m2, 3
We may assume that a3 = (x, y, z) with z > 0.
So these equations become
- x2 + y2 + c x32 = 1
- (x, y, z)
 (1, 0, 0) = - cos (1, 0, 0) = - cos  /m1,3 /m1,3
- (x, y, z)
 (-cos (-cos  /m1, 2, sin /m1, 2, sin  /m1, 2, 0) = - cos /m1, 2, 0) = - cos  /m2, 3 /m2, 3
or
- x = - cos
 /m1,3 /m1,3
- cos
 /m1, 3 cos /m1, 3 cos  /m1, 2 + y sin /m1, 2 + y sin  /m1,2 = - cos /m1,2 = - cos  /m2, 3 /m2, 3
- cz2 = 1 - x2 - y2
Proposition 11.
Let r = 1 - 1/m1, 2 + 1/m1, 3 + 1/m2, 3.
Then
- if r < 0 then c > 0 and W is finite;
- if r = 0 then c = 0 and W stabilizes a half-plane, and it acts by affine
reflections on a plane parallel to its boundary;
- if r > 0 then c < 0 and the group acts by non-Euclidean reflections.
Proof. It all depends on how  - -  /m2, 3 compares to /m2, 3 compares to
 /m1, 2 + /m1, 2 +  /m1, 3. For example, if they are equal, then
the cosine sum formula allows us to set y = sin /m1, 3. For example, if they are equal, then
the cosine sum formula allows us to set y = sin  /m1, 3.
This gives us x2 + y2 = 1,
c = 0, z arbitrary. The group preserves the whole (x, y) plane.
Etc. /m1, 3.
This gives us x2 + y2 = 1,
c = 0, z arbitrary. The group preserves the whole (x, y) plane.
Etc.
Here is a table of cases of possible values of the mi, j
in weakly increasing order:
| Finite: |
2, 3, 3; |
2, 3, 4; |
2, 3, 5; |
| Affine: |
3, 3, 3; |
2, 4, 4; |
2, 3, 6; |
The regular solids
The classification of the finite Coxeter groups in three
dimensions is intimately related to
the classification of the regular solids.
Exercise 14.
Verify that the Coxeter subgroup with values of m
equal to 2, 3, 3 is the symmetry group of the regular
tetrahedron.
Exercise 15.
Verify that the Coxeter subgroup with values of m
equal to 2, 3, 4 is the symmetry group of the
cube and the regular octahedron.
2, 3, 4
Exercise 16.
Verify that the Coxeter subgroup with values of m
equal to 2, 3, 5 is the symmetry group of the icosahedron
and the dodecahedron.
Exercise 17.
Prove directly that the symmetry group of any
regular polyhedron is a Coxeter group.
Exercise 18.
Verify that the symmetry group of the regular simplex in
n dimensions is a Coxeter group.
Exercise 19.
Verify that the symmetry group of the cube in
n dimensions is a Coxeter group.
Affine Coxeter groups of rank 3

|
|
Affine A2
|
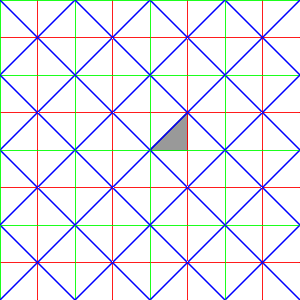
|
|
Affine B2
|
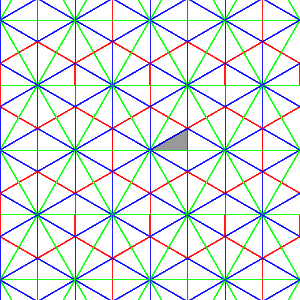
|
|
Affine G2
|
A hyperbolic Coxeter group of rank 3
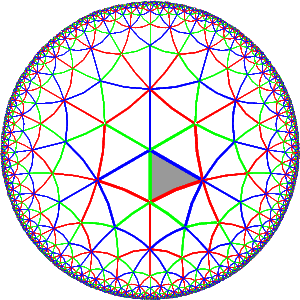
|
|
Poincaré model
|
|
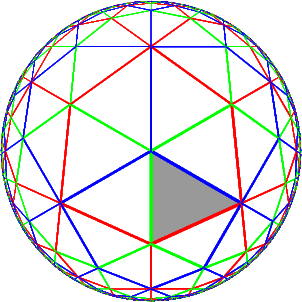
|
Klein model
|
|
|
A polyhedral realization of a Coxeter group
is a linear representation in which
- The group possesses a fundamental domain C
which is a polyhedral cone;
- the generators in S are represented by reflections in the walls of
this cone.
I do not exclude the case where the cone is invariant under translation.
This for a group with a single generator a single hyperplane
is admissible in any dimension.
In these notes, we shall use only
simplicial realizations
where the polyhedral cone is simplicial, its walls
parametrized by S. The dimension of a simplicial realization
must be at least the rank of the group.
Every Coxeter group possesses at least
one realization, as we shall see
in a moment.
Geometric properties of realizations translate naturally to
combinatorial properties of the group. From the geometry
of the simplices neighbouring a fundamental
domain, for example, you can read off the Coxeter matrix.
This is because if L the intersection of two walls, then the configuration
in the neighbourhood of L is
essentially that in a realization of the group
generated by the two reflections in those walls.
This is a special case of a very general result
proven in most generality by MacBeath around 1964.
Given a realization, make a choice for each s in S of a
pair as, asv defining reflection in
the wall of the fundamental domain parametrized by s.
The sign of each function as
can (and always will) be made so that as > 0 in the interior
of the given fundamental domain. Such a linear function as is
determined up to a positive scalar multiple, and its equivalence class
under such multiplications will be called a basic root of the realization
(and implicitly also of the choice of fundamental domain).
The half-space As where as > 0 is determined by this class,
and will be called
a basic geometric root of the realization.
The hyperplane as = 0 will be called a basic root hyperplane.
This terminology is not common, but for
general Coxeter groups this notion of
root is entirely natural, since the particular choice
of as has no intrinsic significance. This is not the case
if the Coxeter group is the Weyl group
of a Kac-Moody Lie algebra,
since in that case the roots themselves
are part of the structure of the Lie algebra.
The Cartan matrix associated to
a choice of functions as is the matrix cs, t = < as, atv >.
If the as are chamnged to dsas then cs, t is cahmnged
to ds cs, t dt-1. This gives rise to a new matrix
DCD-1 where D is a diagonal matrix with
positive entries. But the numbers ns,t = cs, tct, s
depend only on the realization itself. The next result
is a consequence of observations made earlier about
conjugacy classes of pairs of reflections:
Theorem 12. In any realization, the Cartan matrix satisfies these conditions:
- cs, s = 2;
- cs, t = 0 if and only if ct,s = 0;
- cs, t is either 0 or a negative number;
- if ns, t lies between 0 and 4 then
it is equal to 4 cos2 (
 /ms, t). /ms, t).
This theorem is apparently due originally to Vinberg.
A real matrix C satisfying these conditions
for a given Coxeter matrix is called an abstract Cartan
matrix. It determines
a Coxeter matrix in a natural way. The numbers
ns, t will always be non-negative; the finite
values of ms, t are determined by conditions
(2) and (4) for the
values of ns, t lying in [0, 4); and ms, t is
infinite for n which are 4 or larger.
Any Cartan matrix clearly gives rise to a representation
of the associated Coxeter group. In fact:
Theorem 13. The representation of a Coxeter group
determined by any abstract Cartan matrix is a realization of
the associated Coxeter group.
This will be proven in the next section.
One consequence is that every Coxeter group has at least one realization, since there
exists always the standard Cartan matrix
cs,t = -2 cos( /ms,t) . /ms,t) .
Cartan matrices with integral matrices determine
Kac-Moody Lie algebras. In this case the representation
of its Weyl group on the lattice of roots is the one associated to this Cartan matrix.
Coxeter groups which occur as the Weyl groups
of Kac-Moody algebras are called crystallographic,
and are distinguished by the property
that for them the numbers ms, t are either
2, 3, 4, 6 or infinite.
Two Cartan matrices C1 and C2
will give rise to
isomorphic representations of
a Coxeter group
if and only if there exists a positive diagonal
matrix D with C2 = D C1 D-1.
In particular, those Cartan matrices giving rise to realizations equivalent to
the standard one are symmetrizable.
Proposition 14.
If each ms, t is finite, then the isomorphism classes of
Cartan realizations are parametrized by H1(  , R)
(where , R)
(where  is the Coxeter diagram). is the Coxeter diagram).
Proof.
If all ms, t are finite, then
all Cartan matrices are of the form
cs, t ds, t where cs, t = -2 cos2 /ms, t
and ds, t is an arbitrary matrix of positive
real numbers with dt, s = 1/ds, t.
Two of these will give isomorphic represntations of W
when the entries differ by factors ds/dt, with all ds > 0.
But the assignment of ds, t to (s, t) defines
a cocycle on the Coxeter graph with values in the multiplicative group
of positive real numbers, and assignments ds/dt are
coboundaries. Conclude by applying the logarithm. /ms, t
and ds, t is an arbitrary matrix of positive
real numbers with dt, s = 1/ds, t.
Two of these will give isomorphic represntations of W
when the entries differ by factors ds/dt, with all ds > 0.
But the assignment of ds, t to (s, t) defines
a cocycle on the Coxeter graph with values in the multiplicative group
of positive real numbers, and assignments ds/dt are
coboundaries. Conclude by applying the logarithm.
Corollary. If W is finite,
then the Coxeter diagram has no circuits.
Proof. Because if the diagram were not a tree, the group would possess
a continuous family of non-isomorphic representations of dimension r.
Distinct classes can give rise
to realizations with very different geometric properties.
We have seen this already in the case of the infinite
dihedral group,
and here are the pictures for two
different realizations of the Coxeter group whose Coxeter
diagram is 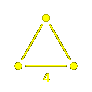 : :

|
|
The Klein model of the standard realization
|

|
|
The Kac-Vinberg realization
|
The first of these is associated to the standard Cartan matrix,
and the second to the integral matrix

which is that of a certain hyperbolic Kac-Moody Lie algebra.
It is the second, therefore, which is likely to have intrinsic significance.
Exercise 20.
Does the Coxeter group of rank 3 with all ms, t = 3 have
non-equivalent Cartan matrices?
Exercise 21.
(This is a research problem! ) Prove that the boundary
of the second is non-smooth everywhere
(i.e. even though it does have tangent lines everywhere, it
will not likely be C2). (This conjecture is consistent with,
but not directly related to, a curious result of Kac & Vinberg,
which asserts that if the boundary of the slice
we are looking at is smooth, it is an ellipse.
This problem will appear more reasonable after we have looked at the role
of finite automata in the geometry
of Coxeter groups.)
|
|
For the moment, fix a Cartan matrix.
It gives rise to a representation of its associated Coxeter group,
in which the elements of s act by reflections.
This will be called for the moment a Cartan representation.
The principal result connecting combinatorics and the
geometry of a Coxeter group is this:
Theorem 15. Suppose w in W, s in S. Suppose that
as is a basic root in
a Cartan representation of W. Then sw > w if and only if
wC lies entirely in the region as > 0.
This generalizes what we have already seen for groups of rank two.
The proof is somewhat intricate.
Proof. It begins with
Lemma.
If T is a subset of S and
w is any element of W, then
there exists u in WT and x in W
such that (a) tx > x for all t in T;
(b) l(w) = l(u) + l(x).
This result will be made more precise later on,
where we discuss the cosets WT\W in more detail.
Proof of the Lemma. The following algorithm
computes u and x:
x := w
u := 1
while tx < x for some t in T
x := tx
u := ut
Since the length of x decreases in every iteration of
the loop, the algorithm certainly stops. When it does so,
tx > x for all t in T. In order to prove
the Lemma, it suffices to verify that conditions (b)
and (c) hold, and also that w = ux, whenever entry into the loop
is tested. They certainly hold at the first test, so it
remains to see that they are not destroyed
in the loop. Equality w = ux is certainly preserved.
Since l(w) = l(u) + l(x) to start
and l(w) = l(ut tx), we also have
l(u) + l(x) is at most l(ut) + l(tx).
But since tx < x, ut > u, and we must have
l(ut) + l(tx) = l(u) + l(x). Thus at the end of the loop
we still have l(w) = l(u) + l(x).QED
We now prove Theorem 3 by induction on l(w).
If w = 1 there is no problem. Suppose l(w) > 1.
If x = sw < w it must be shown that
as is negative on wC. But then wC = sxC;
by induction as is positive on xC,
hence sxC lies in the region where as < 0.
Now suppose sw > 0. It must be shown that
as > 0 on wC.
Choose t such that tw < w. Find u in
Ws,t and x in W satisfying the conditions of the Lemma.
Since tw < w, l(x) < l(w). Since sx > x and tx > x,
induction lets us see that
xC is contained in the region Cs,t where as > 0 and at > 0.
Since l(w) = l(u) + l(x), l(su) = l(u) + 1,
and this is still valid if l is the length
in Ws,t. From the discussion on groups
of rank two, we see that as > 0 on
the region uCs,t, hence on wC = uxC as well.
QED
|
|
A root
of a realization is the transform of one
of the basic roots by an element of W.
If b = w(as) is a root
then g s g-1 is reflection in the hyperplane
b = 0. Thus if b is a root so
is -b. The fundamental chamber C
of the representation is the intersection of all the root
half-spaces as > 0.
A root is called positive
if it contains the chamber C,
negative if its opposite contains C.
Proposition 16. Every root is either positive or negative.
The point is that the chamber C is not intersected by
a root hyperplane.
This result follows immediately from Theorem 3. A reformulation:
Proposition 17. If wC intersects C then w = 1.
Proof. If w is not equal to 1, then there exists s
with sw < w. But then C and wC lie on opposite
sides of the hyperplane as = 0.
In other words, every Cartan representation is a realization of the group
as a subgroup of GL(V). If we restrict the realization to
the subgroup generated by T, we see that
WT embeds into W, too.
For a subset T of S, let CT be the region in
the boundary of C where the basic roots at = 0 for
t in T, as > 0 for s not in T.
Every point of CT is fixed by t in T,
hence all elements of the subgroup WT. Conversely:
Proposition 18. 3. Let  be the closure of C.
If w be the closure of C.
If w intersects intersects  then the intersection equals the closure of
CT for some T, and w lies in WT. then the intersection equals the closure of
CT for some T, and w lies in WT.
Proof. By induction on l(w). If w = 0 or 1, no problem. Otherwise,
say sw < w and w = sx for l(x) < l(w). Then as  0 on x 0 on x while aa
while aa 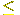 0 on w 0 on w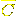 . Therefore the intersection
of C and wC lies in as = 0. But then
the intersection of x . Therefore the intersection
of C and wC lies in as = 0. But then
the intersection of x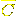 and and 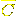 is non-empty,
so we can apply the induction hypothesis. We deduce
that the intersection of x is non-empty,
so we can apply the induction hypothesis. We deduce
that the intersection of x and and  is equal to the
the closure of some CT, and x lies in WT.
But then sC intersects CT as well, and s lies in T also.
Hence w lies in WT. is equal to the
the closure of some CT, and x lies in WT.
But then sC intersects CT as well, and s lies in T also.
Hence w lies in WT.
Corollary. Any face of a chamber of a realization
is the W-transform of a unique face of C.
Proof. If xCU = yCT, then y-1xCU = CT.
But then y-1x must lie in WT.
In other words, each face of a chamber is labeled by
a unique subset T.
A gallery is a sequence of chambers Ci
with each successive pair sharing a face of codimension one. If
w = s1 ... sn then the sequence
C, s1C, s1s2C, ... , s1s2 ... snC is a gallery.
The chambers C and sC share a face labeled by s, and hence
wC and wsC do, too. Minimal galleries correspond to reduced words.
For w in W, let Lw be the set
of positive roots r such that w-1r is negative - i.e. r > 0
on C but r < 0 on wC. This means that the root hyperplane r = 0
separates C from wC. In any gallery
linking C to wC it must be one of the walls
between two successive chambers in the gallery. Therefore:
Proposition 19. The root hyperplanes for r in Lw
are those separating C from w-1C.
A minimal gallery from C through xC to xyC can be split into
two disjoint pieces, one from C to xC, the other from
xC to xyC. The second is the x-transform by x
of a gallery from C to yC. Therefore:
Proposition 20. If l(xy) = l(x) + l(y) then
Lxy is the disjoint union
of Lx and xLy.
Corollary. The length l(w) is the cardinality of Lw.
Corollary. The length of w is the number of root hyperplans
separating C from wC.
Proposition 21. An element w lies in WT if and only if
Lw is contained in T.
Let R+ be the set of positive roots,
RT those generated by WT from the at with t in T.
Proposition 22.
An element of WT permutes the roots in R+ - RT+.
Proposition 23. A reduced word for w in WT is one also in
W.
Proposition 24. In every coset WT \ W there exists a unique element
x such that tx > x for all t in T. For any w in this coset,
l(w) = l(wx-1) + l(x).
Let WT be the set of these distinguished coset representatives.
Proposition 25. Any element w can be expressed as w = xy
with x in WT and y in WT.
These last will be left as exercises.
|


 / m
/ m


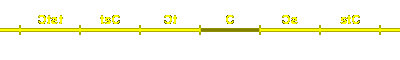


 /ms,t) .
/ms,t) .