Mathematics 309
Part II - Introduction to light
2. Simple refraction
When light passes from one substance to another, it changes direction. This effect is familiar to all of us from observations in bath tubs and swimming pools, and it is called refraction. The effect is usually dealt with as if light were rays that literally bend in direction as they pass through the boundary, but in fact the elegant explanation of what happens relies on the wave theory of light.Light travels at a finite constant speed in every homogeneous substance, at some fraction of the velocity with which it travels in a vacuum. In a substance S the index of refraction nS is the inverse of that fraction, which is therefore a number greater than or equal to 1. It varies with the colour of the light (this effect is called dispersion), and it is generally larger for blue light than red (which has the lower frequency). Of course in air this index is very close to 1, but in water it is about 1.33 for red light and about 1.34 for blue.
Snell's Law
Here is the effect of refraction explained in terms of rays. A ray strikes the surface between substance Si and substance Sr. The angle i between the first ray and the normal vector at the boundary is called the angle of incidence, and the angle r between the second and the normal vector on the opposite side is called the angle of refraction.
Snell's Law says that ni sin i = nr sin r. For red light in air hitting water this gives sin r = sin i/1.33
This rule has a peculiar effect on obesrving the world above the surface of water when viewed from below.
Huygen's explanation
It turns out that Snell's Law is a simple consequence of the assumption that light ravels in waves perpenicular to the apparent direction of the rays. The geometry of the wave motion changes from one substance to another, but the period (or frequency) of the waves cannot change. Since
ci = 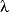 i/T
i/T
cr = 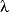 r/T
r/T
T
= 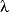 i/ci
=
i/ci
= 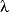 r/cr
r/cr
so that the ratio ni/nr
of velocities is the same as
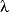 i/
i/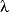 r.
By the geometry of the way the waves on each side meet at the boundary
r.
By the geometry of the way the waves on each side meet at the boundary
sin i = 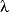 i / d
i / d
sin r = 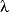 r / d
r / d
d = 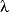 i / sin i =
i / sin i = 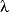 r / sin r
r / sin r
Explicit calculations
In tracing rays of light through an optical system, it will be important to have at hand several simple conventions. First of all, a ray is determined by an initial point P together with a direction vector v, which we shall assume to be of unit length. The ray itself will be the half line we get by parting from P in the direction of v and going off to infinity. This is the set of all points P+tv where t is a non-negative scalar. When the ray hits the boundary between two different substances, it will refract, and begin a new ray.
The new point P* will be the point where it hit, and the new direction v* the one determined by refraction.
The direction v* is determined from v by rotation through i-r. In the image above, this is in a clockwise direction, but exactly how it works in general must be explained more carefully.
Let n be the unit vector perpendicular to the boundary where the ray hits, the one that lies in more or less in the same direction as the ray. Let n* be what you get by rotating it through a right angle counter-clockwise. Then we can write v as a sum of components parallel to n and n*.
In fact v = (cos i) n + (sin i) n* . The angle i can be calculated from this, since cos i and sin i are thus also the dot products v . n and v . n*. And finally v* = (cos r) n + (sin r) n* .
Summary of how to calculate v*
- Find the unit vector N perpendicular to the boundary facing in the direction of the ray. Calculate N*, which is equal to the rotation of N by 90 degrees in the plane spanned by N and v.
- Calculate v . N and v . N* to get cos i and sin i, then i.
- Let r = arcsin(ni sin i / nr ).
- Then v* = (cos r) N + (sin r) N*.
- Alternatively, calculate the rotation of v by i-r in the negative direction relative to N and N*.