Mathematics 309
Part I - The elementary geometry of wave motion
3. Affine functions
Two dimensions
An affine function in 2D is a scalar-valued function of the form Ax+By+C. The level curves of the function are the curves where the function takes a fixed value. For example, if the function is x+y then some of the level lines look like this:
Of course the level lines of the function Ax+By are the same as those of Ax+BY+C, but with different constants. So we may as well assume C=0, and the level lines are of the form Ax+By=k. If the coefficient B is not 0 then the equation Ax+By=k can be solved to get the equation y = (k-Ax)/B, the more familiar equation from elementary mathematics. From this equation we can figure out the slope and the y-intercept, and then plot the curve, which is actually a straight line. The level curves that escape thsi are those where B=0, or x=k/A, which are vertical. But it is unnecessary to distinguish cases. Here we want to explain more directly the geometric properties of the level curves.
- The line Ax+By=k is perpendicular to the vector [A,B].
- The distance of the line Ax+By=k from the origin is |k|/| [A,B] |.
- The line Ax+By=k lies on the same side of the origin as the vector [A,B] precisely when k > 0.
The line x+y=1 is perpendicular to [1,1],
on the same side of ther origin as [1,1],
and at distance 1/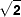 from the origin.
from the origin.
< Why are these things true?The first on eis easy. If P = (Px, Py) Q = (Qx, Qy) are points on the line AX+By=k, then
A Px+B Py=k
A Qx+B Qy=k
A(Px-Qx)+B(Py-Qy)=0
which means that the dot-product of [A,B] and P-Q equals 0, or that they are perpendicular. Since P-Q lies in the direction of the line, that's the first assertion.
There will be a unique scalar multiple t[A,B] which lies on the line Ax+By=k. This will be the case when
A(tA)+B(tB) = t(A2+B2) = k
t = k/(A2+B2).
The length of the vector t[A,B] is then k/| [A,B] |, and this proves the second assertion. The last one follows from the sign of t, i.e. of k.
Three dimensions
An affine function is of the form Ax+By+Cz+D. The points (x,y,z) where this has a constant value is a plane Ax+By+Cz+D=k. Here:- The plane Ax+By+Cz=k is perpendicular to the vector [A,B,C].
- The distance of the plane Ax+By+Cz=k from the origin is |k|/| [A,B,C] |.
- The line Ax+By+Cz=k lies on the same side of the origin as the vector [A,B,C] precisely when k > 0.