
Laser eye surgery has become increasingly popular to help those with shortsightedness. Many have underwent this procedure and are able to see without glasses. But one of the side effects of corrective eye surgery is the occurence of seeing halos around lights at night time. This makes it difficult for one to see clearly at night.

|
The follow picture illustrates how a halo around a light at night time would appear to a person with eye surgery |

|
A normal person without eye surgery, looking at the same light would see a a much clearer view. |
To understand this phenomena, we'll first look at how the eye works and then a shortsighted person's eye, before they undergo any surgery.
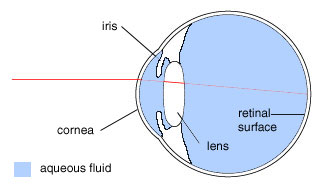
The eye has a transparent, outer surface at the front called the cornea. This is where light enters the eye. The cornea is spherical in shape, allowing it to refract light.
The iris acts like an aperature, narrowing or widening its circular opening, controlling the amount of light that enters the lens. The lens acts as an optical lens that can change its curvature to refract light rays by different amounts, so an in-focus image forms at the retinal surface. The image at the retinal surface is interpreted by the brain to create the image one sees.
The remaining interior of the eye is filled with aqueous fluid, having a composition close to water.
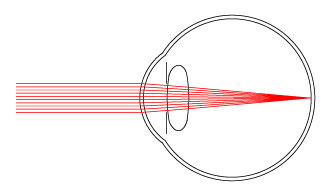
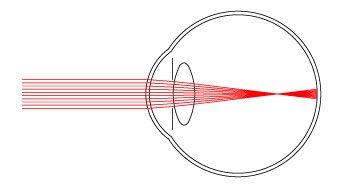
As light rays hit the cornea, they refract and bend towards the center. This is because of Snell's law, so light rays going from the air to the cornea, refract towards the surface normal, because light travels slower in the cornea and has a higher index of refraction that air. When the rays reach the lens, they are refracted again and focus on the retinal surface at the back of the eye. Light rays from a distance object are focused to one point that lies on the retina, creating a sharp image.
To mathematically model the eye as a system of optical lenses, we'll use a linear approximation involving matrices.
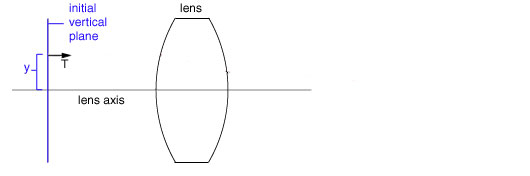
Each ray starts at an initial vertical plane and has a height y on the plane, and angle q between the ray and lens axis. For further simplification, we replace the direction q with T = nq , where n is the current index of refraction. Thus (y,T) is a ray starting at the vertical plane.
A linear matrix can be used to describe the transformation of a ray (y, T), as it refracts at a surface or travels (translates) through a medium.
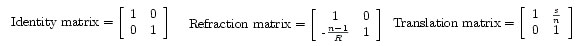
In the refraction matrix, n = current index of refraction, R = radius of curvature of the lens, with a positive curvature being convex to the left. In the translation matrix, s = horizontal distance the ray travels, and n = current index of refraction.
We apply our matrices as follows. Our new ray (y*,T*) is computed by applying it to one of the above matrices.
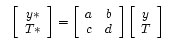
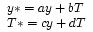
So the ray (y,T) = (0.4, 0) in the previous picture, has the index of refraction in air n = 1.0 and the radius of curvature of the first lens surface R = 1. The resulting refracted ray is
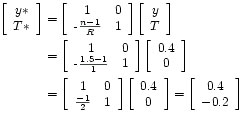
So the path of ray so far look like:
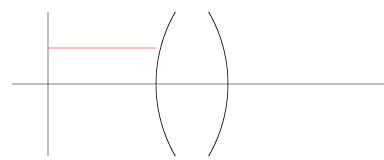
If we continue with the computation, we get the following picture, showing where the ray eventually will focus.
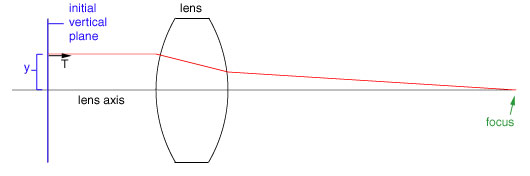
The myopic eye can't focus light from far away, (parallel light rays (y,0) ), but can focus light from close objects. Since the lens in the eye cannot change its curvature enough to focus light rays at the retina, we'll look at changing the curvature of the cornea, which is done in refractive eye surgery.
The 4 matrices describing the refraction at the outer and inner surface of the cornea and translation of rays through to the lens are shown below. M is the transfer matrix describing the cornea.
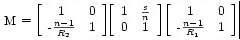
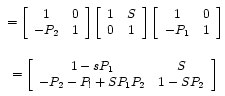
The index of refraction of the cornea is 1.37 and its outer radius of curavature, R1 = 7.8mm. Its inner radius of curvature is smaller than its outer curvature and the corneal thickness is 0.5mm. Given this information, we can compute the values of P1, P2 and S, in the matrix and the final matrix for the cornea.

The corneal lens matrix M, will be represented by the matrix to help simplify the notation.
To understand how a myopic eye focusses light, we'll look at conjugate planes. The light at a point on an object infront of the eye focusses at some point on the retina, so these two points define the conjugate planes for each other. Two planes are conjugate if light from a point on one plane focusses on some other point on the other plane.
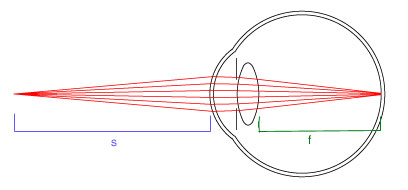
To see why the focus in a myopic eye is infront of the retina, we must look at the lens system for conjugate planes. The resulting transfer matrix for this conjugate plane system is
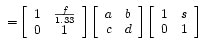

In terms of matrices, incoming light rays have a height y = 0, and a resulting height y* = 0. So in terms of the resulting transfer matrix.
Ay + BT = y* = 0
BT = 0 so B = 0 because y* is independent of T , since changing T has no effect on y*.
Now we solve B=0 from the conjugate plane matrix and derive a formula for the focus in terms of the object's distance s.
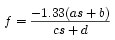
Substituing in for a,b,c and d the values of the corneal lens system, the focal equation becomes:
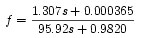
We can see that as you increase s, the distance between the object and the eye, the denominator increases quicker than the numerator, so f, the focal distance decreases. So as a short-sighted person attempt to view objects further away, the image will focus a some point infront of the eye, creating an out-of-focus image on the retina
So how does flattening the cornea help one to focus light from far away so they are in-focus at the retina? Lets look at the matrix describing the focus of the corneal lens.

Since we have parallel rays from infinity, T = 0 and the resulting rays focus at some point where y* = 0. So
in terms of the transfer matrix for the system
Ay + BT = y* = 0
Ay = 0, so A=0
Solving for A = 0, the upper left term in the transfer matrix, we get the following focal equation for the corneal lenses.
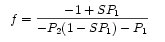
If we wish to make f, the focal length larger, so that the image will focus at the retina, we can try to change P1, by changing R1, the radius of curvature for the outer surface of the cornea. As we flatten the cornea, R1 increases making P1 decrease.
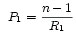
SP1 and SP2 are small terms since S is minute in value, so we can ignore these terms when considering the effect of changing P1. As P1 decreases, the denominator becomes less and less negative. Since the numerator is dominately negative, f increases positively as P1 decreases. This is why laser eye surgery flattens the cornea to obtain a greater radius of curvature in the outer cornea. The amount by which you flatten the cornea depends upon the required curvature needed to focus light properly at the retina.
This is what the cornea look like after surgery: The central cornea is flatter than the peripheral corneal, so light focusses correctly at the retina.
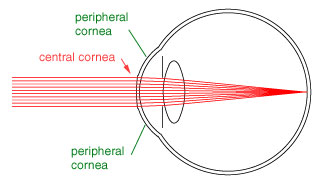
Now we look at how this relates to halos. The iris acts like an aperature that restricts the amount of light that reaches the lens and eventually the retina. If the eye is receiving alot of light, the iris constricts itself to reduce the amount of light entering. If it's dark, then the iris will open larger to allow more light to enter the eye. Halos around lights are seen when it is dark, because the iris open wider, allowing light from the peripheral area of cornea to reach the lens. Light from these regions will focus infront of the retina, since the eye was original myopic.
To determine what one actually sees, we'll look at where light rays passing through the peripheral regions of the cornea that end up hitting the retina.
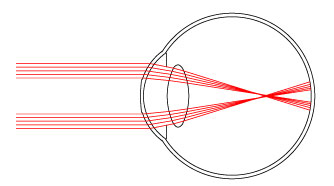
We can see these rays focus at the old focus of the myopic eye, so when they reach the retina, the rays become out-of-focus. The two bands of light rays that reach the retina create the fuzzy, halo of light, as depicted at the beginning of our discussion.
Combining all the rays, refracting through the flattened cornea and the peripheral cornea, one sees the following:
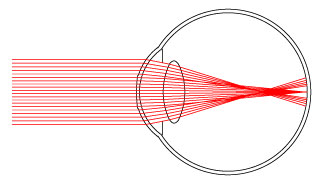
There is a sharp focus of the image of the light source at the retina, so one sees the light unblurred, but the two extra bands of rays, surround the sharp image of the light, blurring the clarity of the light.
Krachmer, Jay H. MD, ed., Basic Science, Refraction, and Pathology (Elsevier Science, 2002).
Azar, Dimitri T., Excimer Laser Photorefractive Keratectomy (Williams & Wilkins 1997).
Seiler, T, Beckmann, W, and Maloney, RK "Effective spherical aberration of the cornea as a quantitative descriptor in corneal opography," Journal or Cataract & Refractive Surgery Vol 19, 1993, (Suppl): 155-165.
Yuan-Chieh Lee, Fung-Rong Hu and I. -Jong Wang "Quality of vision after laser in situ keratomileusis: Influence of dioptric correction and pupil size on visual function," Journal of Cataract & Refractive Surgery Vol 29, Issue 4, April 2003, 769-777.
Birgit Lackner et al., "Glare and halo phenomena after laser in situ keratomileusis", Journal of Cataract & Refractive Surgery Vol 29, Issue 3, March 2003, 444-450 .
Author: Lyndon Hiew
80624992
Created: April 28, 2003