Assignment 2

• Brief notes on PostScript
  
  

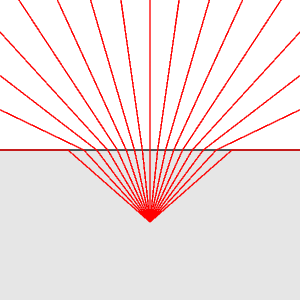
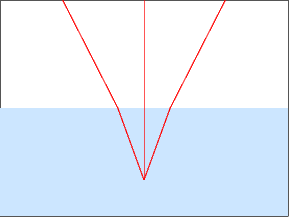
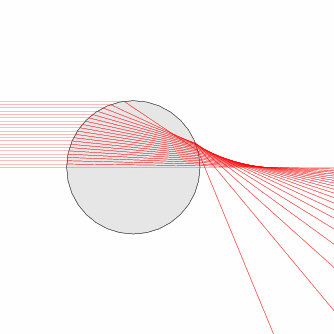
The first picture below shows the paths of ray coming from underwater to the air above. The second shows the paths of rays of red light reflecting inside a raindrop, and the one on the right shows what happens if these same rays pass through. Doing this will involve using the basic commands discussed in the notes above, together with a small collection of special commands designed for the task. They are contained in the file lenses.inc, which you should download onto your machine. Then, at the beginning of your PostScript program you should include the line (lenses.inc) run, which will cause this file to be included in your program if your environment has been set up satisfactorily. This may involve fooling around with the options in your PostScript viewer. For one thing, you should click off the option SAFER in GSView.

The package of procedures in lenses.inc includes commands

• roots
  [A B C] roots returns an array of 0, 1, or 2 roots of the equation A x² + Bx + C = 0, in order. [1 -3 2] roots will leave [1 2] on the stack.

  Many of the routines described here return an array of numbers. There are a number of reasons for this. In order to access the numbers inside, you must give that array a name, and then use get. For example,
  
  /r [1 -3 2] roots def
  r 0 get
  
  defines r to be the array of roots and puts the first on the stack.

• reflection
  n v reflection returns the reflection of the unit vector v with respect to the unit normal vector n. In other words, you use this in the follwoing way: you have calculated the unit normal vector at a point on a surface (say with gradient and normalized, described below). If v is a direction (unit length) vector, n v will leave on the stack the new direction of the reflected ray. As in the discussion of roots above, you'll want to give that new direction vector a name with def.
• refraction
  n v index refraction returns the refracted direction as a unit vector [x y]. (See the discussions of roots and reflection above, too).
• vadd
  u v vadd returns the vector sum of the 2D vectors u and v. Thus
  
  [1 1] [-1 1] vadd
  
  leaves [0 2] on the stack.
• asin
  x asin returns the arc sin of x. You can use this one even in drawing the first (and simplest) picture above, in order to figure out exactly what the minimum and maximum angles in the cone of rays are.
• vscale
  v c vscale returns cv. Thus
  
  [1 2] -1 vscale
  
  leaves [-1 -2] on the stack.
• hit
  [x y] [vx vy] [cx cy] R hit returns the point where the ray P + tv = [x y] + t[vx vy] hits the circle with radius R and centre [cx cy]. The vector [vx vy] is the direction of the ray. This procedure will return an empty array if the ray misses the circle. Thus
  
  /P1 [-5 0] [ 1 0] [0 0] 1 hit def
  
  defines P1 to be [-1 0]. And
• gradient
  [cx cy] [x y] gradient returns the gradient vector at the point [x y] for the function (x-cx)²+(y-cy)². This is changed from an earlier version which had three arguments.
• normalized
  [x y] normalized returns the normalized vector with length 1. These two should be combined with reflection and refraction. Thus
  
  /P1 [-5 0.5] [1 0] [0 0] 1 hit def
  /n [0 0] 1 P1 gradient normalized def
  /v1 n [1 0] reflection def
  
  finishes by letting v1 be the direction of a ray reflected from the unit circle, with centre at the origin, where the horizontal ray from [-5 1/2] hits it.

  PostScript is simple-minded but wordy.

• vlength
  [x y] vlength returns the vector length.
• The package stores the indices of refraction of red and blue light as red-index and blue-index.
• line-intersection
  P v [A B C] line-intersection returns the point where the line through P in the direction of v intersects the line Ax+By+C=0. As an array of two numbers.

A start:

Click on image to see the PostScript source.

In order to understand exactly what this program does, you should read especially the section on the stack in the notes. In order to complete the drawing, you have to figure out what angle is the most extreme one visible from above the pool, the one that corresponds to a ray horizontal along the water surface. Use the law of refraction to figure this out with a calculator, say. We'll talk about all of these things on Monday.

Then to begin on the other two figures. This will require that you import the file lenses.inc into your own file and use the routines defined there.