Math309 Assignment 1 Name: Sandy Chan and Tomoko Kitagawa

Part 2 Wave function in 1D

simple periodic motion can be seen in cosine wave.

Parameters used in here are (wave length): is the distance over which the wave pattern repeats, as measured at a fixed time.
T(period): is the time for one complete wave cycle to pass a fixed position.
(frequency): is the number of wave cycles passing a given point per unit time which is the inverse of the period. Also, it can be described as radians per seconds.
c(velocity): is the distance of the wave travel divided by time interval.
A(amplitude): the maximum value of the disturance. It measures whatever physical quantity is affected by the wave.

Except for A, any two parameters can determine the third.

eg) = cT

= 2c /

c = / T

= 2c ( II-1)

When velocity has a direction (i.e. in a certain number of dimensions like 2D, 3D), the equation ( II - I ) need modification.

In this case, is interpreted as a vector between two crests.

Then,

|c| = || / 2 where c is 'speed', not 'velocity'

at time t,

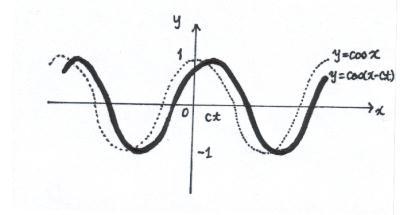
the graph is shifted right by ct
so y = cos (x - ct)
Then,

when graph is scaled horizontally by 1/c,

x → cx

y = cos cx

eg) y = cos x

y = cos 2x

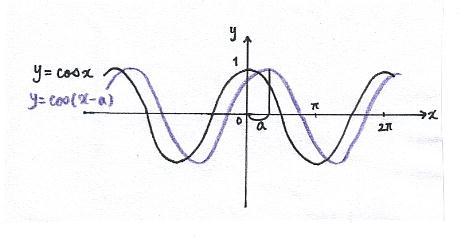
b) When graph is shifted left by a,

x → x - a

eg) y = cos x

y = cos ( x + a)

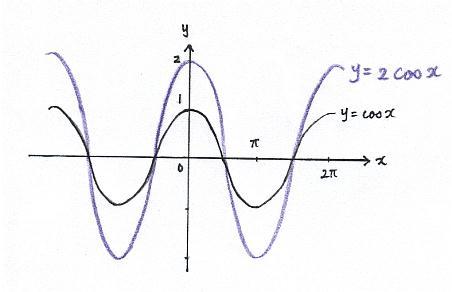
c) When graph is scaled vertically by c,

f = cf

eg) y = cos x

y = 2 cos x

d) When graph is shifted vertically by a,

f = f + a

eg) y = cos x

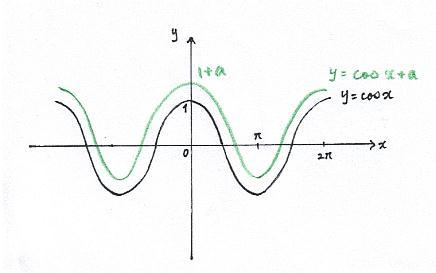
Over, the equation of the wave in 1D is

y = A cos ( 2/ ( x - ct))

= A cos ( 2x / - 2ct / ) where = 2c /

= A cos ( mx - t) where m = 2 /

Part III Affine Function in 2D and 3D

An Affine function of 2 variables is

    Ax + By + C

also, an affine function of 3 variables is

    Dx + Ey + Fz + G
For the wave equation, phases can be expressed in affine functions.

A cos ( ax + by + c - dt) in 2D ( III-1)

A cos ( ax + by + cz + d - et) in 3D ( III-2)

Level lines

A level line is a " curve" such as

Ax + By = constant ( III-3)

Ax + By + Cz = constant ( III-4)

for example, in the equation III-3,

Ax + By = constant

i) when B = 0, Ax = constant

x = constant / A

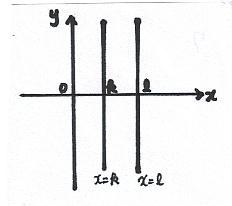
ii) when B≮ 0 , y = constant - Ax / B

= -Ax / B + constant k

For 2D level lines

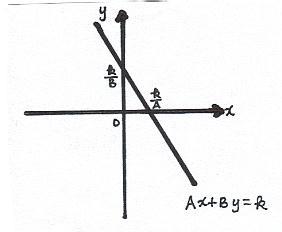
Ax1 + By1 = constant k

Ax2 + By2 = constant k

So, A( x1 + x2) + B ( y2 - y1) = 0

[ A, B ] is perpendicular to [ x1 -x2, y2- y1]

So, the level line Ax + By = k is perpendicular to [ A, B ]

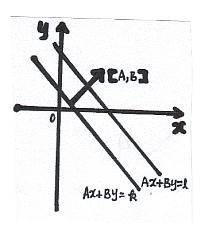
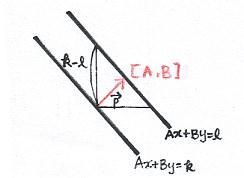
For 2 different 2D level lines with different constant number

Ax + By = k

Ax + By = l

These two lines are parallel and also perpendicular to vector [ A, B ]

Distance between two level lines are

p = [A, B ]

|| p || = 1/≡A² + B²

|| (k-l) p || = k-l / ≡A² + B²

In 3D, the level line is

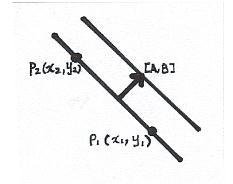
Ax + By + Cz = k

Ax1 + By1 + Cz1 = constant k

Ax2 + By2 + Cz2 = constant k

A( x1 - x2 ) + B( y1 - y2 ) + C( z1 - z2 ) = 0

so, [ A, B, C ] is perpendicular to [ x1 -x2, y1- y2, z1- z2 ]

Therefore, the level line is perpendicular to [ A, B, C ]

p = [ A, B, C ]

is also perpendicular to the level lines and,

= a p

so, || || = a / ≡A² + B² + C²

= k ≡A² + B² + C² where k = a / A² + B² + C²