Mathematics 309- the Elementary Geometry of Wave Motion

Mathematics 309 - the elementary geometry of wave motion

Part I - Scaling and Shifting

One way of obtaining one graph from another is by scaling and shifting either x or y or both, so that the graph y=f(x) becomes the graph y = af(bx + c) + d. The way to see what happens to the graph is to understand what happens in simple steps with just one change at a time.


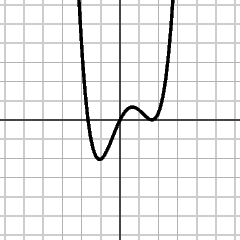
y = f(x)	y = 2f(x) All y-values on the graph are scaled by 2. In subsituting cf for f, vertical distances are scaled by c.

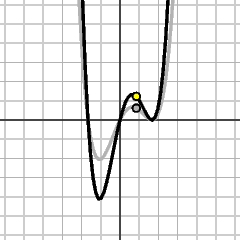
y = f(x)	y = f(x)+1 1 is added to all y values.

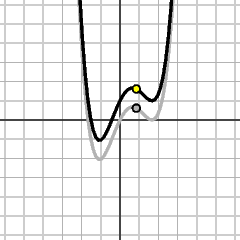
y = f(x)	y = f(2x) The height at x on the new graph is equal to the height at 2x on the old one. The new graph is obtained by compressing the old one horizontally by 2. In substituting cx for x, horizontal distances are scaled by 1/c.

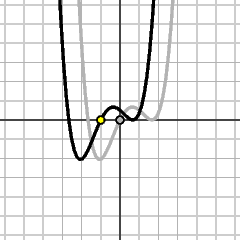
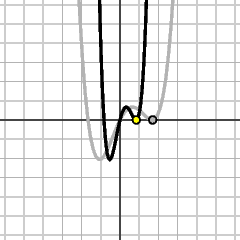
y = f(x)	y = f(x+1) The height at x on the new graph is equal to the height at x+1 on the old one. The new graph is obtained by shifting the old one 1 to the left.

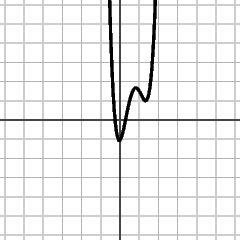
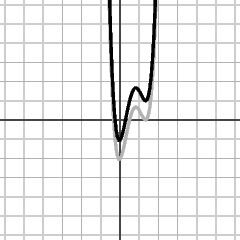
y = f(x)	y = f(2x-1)+1

Only the last one is tricky, since it involves a sequence of substitutions. In order to see which ones, we unravel the process.

The function f(2x-1)+1 is obtained from f(2x-1) by adding 1.
The function f(2x-1) is obtained from f(x-1) by substituting 2x for x.
The function f(x-1) is obtained from f(x) by substituting x-1 for x.

To get the graph, we go backwards. We start with the graph of f(x).

Substitute x-1 for x, y = f(x-1):
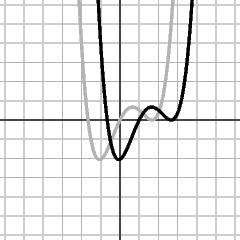
Substitute 2x for x, y = f(2x-1):
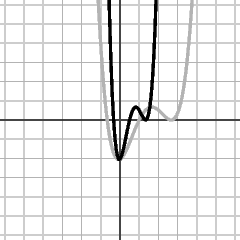
Add 1 to y, y = f(2x-1)+1:

Part II - Wave Functions in 1-Dimension

The waves we will study travel in simple periodic motion.
ie, waves travel with constant period over space and time

Simple waves have a velocity (c), period (T), frequency (w)
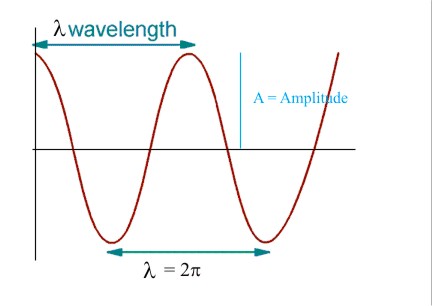
An example of a simple periodic wave is the cosine function, y = cos(x).

wave length l = the spatial distance between 2 crests of the wave.
period T = the time it takes to go through one cycle at a fixed point.
(ie, the time between the passage of two crests) (units: time in seconds)
(angular) frequency w = radians per second.
velocity c = velocity at which the crest travels.
amplitude A = the vertical distance between the reference line/x-axis and the top of the crest.

for example
Suppose the period of a wave is 2 seconds,
then the frequency = 1/2 of a period per second

There are 2 kinds of frequencies

cycles per second

radians per second, w = 2p/T (angular frequency)

we shall focus on the latter.

we know period = T = 1/frequency
so, T = 1/(w/2p) = 2p/w
T = 2p/w

Thus in time T a wave travels l distance
so, c = l/T = l/(2p/w) = lw/2p
c = lw/2p

Now, looking at time t = 0
y = cos(x)
but each motion could be started with different amplitudes
so, y = Acos(x)

what about time t?
at time t, the graph is shifted to the right by ct (which is the distance moved at time t)
thus y = Acos(x - ct)

We know that the function y = cos(x) has a wavelength of 2p.
Thus to scale this function we must scale by l/2p.

so y = cos(x/(l/2p)) = cos(2px/l)
y = cos(2px/l)

Now, putting all this together:

y = Acos{(2p/l) (x-ct)}
y = Acos(2px/l - 2pct/l)
recall: 2pct/l = 2p/l * lwt/2p = wt

This gives us the Fundamental Wave Equation, which is

y = Acos(2px/l - wt)

Part III - Affine functions in 2D & 3D

Definition:
A function A: R^m ® Rⁿ is affine if there is a linear function L: R^m ®Rⁿ and a vector b in Rⁿ such that

A(x) = L(x) + b, for all x in R^m.

An affine function is just a linear function plus a translation. From our knowledge of linear functions, it follows that if A: R^m ® Rⁿ is affine, then there is an n*m matrix M and a vector b in Rⁿ such that

A(x) = Mx + b, for all x in R^m.

In particular, if f: R ®R is affine them there are real numbers m and b such that

f(x) = mx + b, for all real numbers x.

Part A - Affine function in 2D

An affine function

Ax + By + C = 0 (function of 2 variables)

A & B are considered the linear component and C is the vector added (translation). This affine function is a transformation of the plane, it takes lines to lines and parallel lines.

Note: Ax + By + C = 0 matrix multiplication of

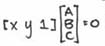
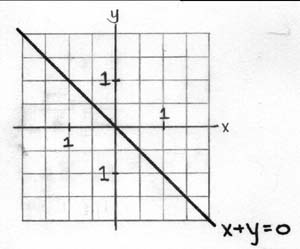
Take the simpliest case of setting C=0 (Ax + By = 0) and draw the level lines

[note: the level lines of Ax + By are all perpendicular to [A, B] which will be explained later]

And in the case of C¹0:

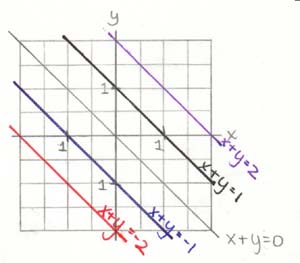
If we take our function Ax + By + C = 0 and take the cases B=0 and B¹0, we get: B=0: Ax=C => x=C/A

vertical lines

B¹0: y= (C-Ax)/B => (-A/B)x + C

non-vertical lines

But we want a uniform way to describe the level lines of Ax + By without separating into cases B=0 & B¹0.
If we look again at the case of C=0: Ax + By = 0
[A,B] × [x,y] = 0
[A,B] ^ [x,y]

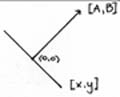
(line through origin ^ to A B \ explaining why the lines of Ax + By are all ^ to [A B])

A level line is a curve where a function has a single value. The "curve" Ax + By = 0 is the line through the origin ^ [A,B]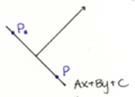

Ax + By = C

Ax_* + By_* = C

A(x -x_*) + B(y-y_*)=0

Using P_(x_,y_*) and P(x,y)

If we go back to the example of the function Ax + By + C = 0.

The line Ax + By = C is ^ [A,B] and at signed distance C /(Ö(A²+B²)) from the line Ax + By = 0, C > 0 if the line is in the direction of [A,B]
For example: If we take C₁, C₂:

Ax + By = C₁

Ax + By = C₂
To find the signed distance between them we use the formula: (C₂ - C₁) / (Ö(A²+B²))

Example

If we take the wave height equation (where A is the Amplitude):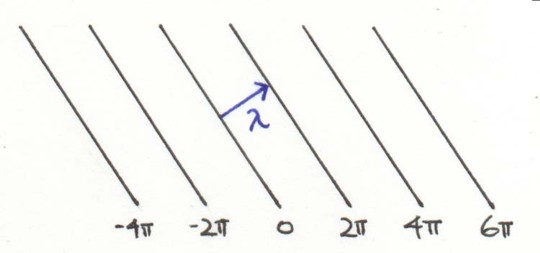

A cos (mx-wt)

A cos (ax + by + ct)

We note that the wave length vector l is perpendicular to the level lines and is a multiple of [a,b].

The signed distance from 0 to 2p

||l|| = 2p/(Ö(a²+b²)) = k(Ö(a²+b²)) when k[a,b]

k = 2p/(a²+b²)

l=( 2p/(a²+b²)) [a, b]

At time t=0, the wave height = A cos (ax + by) where [a,b] is related to l (wave length vector).
It changes with time because

A cos (ax + by - wt)

(where w = radian frequency) Thus the wave (radian frequency) is a function of space and time.

Part B - Affine functions in 3D

Affine functions in 3D is similar to 2D. We are dealing with planes on a graph not lines because there are 3 variables not 2. However, the 2D graph is like a cross-section of the 3D graph.
We have the function Ax + By + Cz + D = 0.

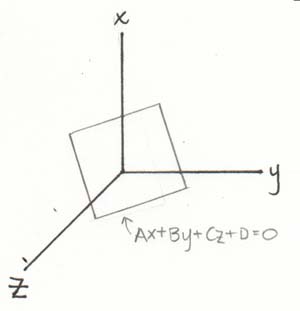
l is a multiple of [A, B, C] therefore the sign distance from 0 to 2p
||l|| = (2p - 0)/ (Ö(a²+b²+c²)) = 2p/ (Ö(a²+b²+c²)) = k(Ö(a²+b²+c²)) (where l = k[a,b,c])

k = 2l/(a²+b²+c²)

l = (2p/(a²+b²+c²)) [a, b, c]
At time t=0, the wave height = A cos (ax + by + cz) where (a,b,c) is related to l (wave length vector). It also changes with time since the wave is a function of space and time A cos (ax + by + cz - wt), where w-radian frequency.

Wave Motion in 2D and 3D

As seen in 1D, the wave equation is Acos(2(p/l)(x-ct)).
Where A is the amplitude of the wave, and c is the velocity of the wave.
Wave motion in higher dimensions follow similar properties as of those in 1D and thus we can study them as in one dimension.
When the wave travels, a cycle is measured by the distance between the crests of the wave.
The equation wl=2pc allows to solve for w, the time frequency or l, the wave distance.

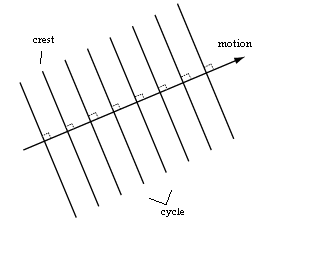
The height of the wave is a function of space and time: Acos(ax + by + cz - dt) where b*y is the phase of the graph.
If the displacement is not zero, two points along the a wave have the same phase if their displacements are the same.

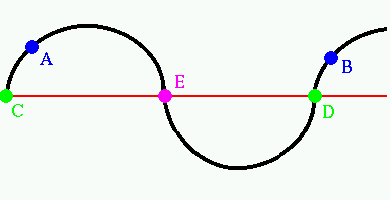
In the diagram A and B have the same phase, as do C and D. But E does not have same phase as A, B, C, or D