, 
, c, A.
They are the fundamentals of a wave or else it would not be classified as a wave. They'll be explain in more detail.
by Perry Cheng
st:88237011
Topics Covered:
Scaling and Shifting Graph
To know more about scaling and shifting a graph please go to this link: Click Me!
Wave Functions in 1D
All waves in the first dimension are all classified with these basic parameters: , , c, A.
They are the fundamentals of a wave or else it would not be classified as a wave. They'll be explain in more detail.
)
)
The Frequency is the number of complete wave cycles occurring per unit
time. But we are instead switching from cycles per second to
radians per second. Since 1 cycle in a wave, usually takes 2p
in order to complete one cycle, so in order to change it from
cycles per seconds to radians per second, we need to multiply a 2p
to the original 1/T where T is the period it takes to complete a
cycle: 
The Velocity c is the velocity at which the crests travel. 
The Amplitude is just the Height of the wave.
The wave equation has all the basic parameters of a wave as we have discussed before.
Within the wave equation it has a height of A, shifted by ct (*distance = velocity x time), with the width of
the wave scale by a multiple of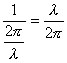 
. A sample picture:
Recall the Affine Function in 2D is: Ax + By + C. An affine function in 2D is basically a line,
that has a normal vector [A, B]. The normal vector is perpendicular to the level lines of
Ax + By + C = 0 or Ax + By = C {* y = (C - Ax)/B where B not equal to
zero}. It is perpendicular because when Ax + By = 0, it is just the dot
product between the vectors [A, B] and [x, y], and any dot product that is equal
to zero is orthogonal (or perpendicular). A sample picture:
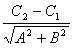so in our example, its from 0 to C: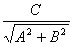 
In 3D, the function behaves the same way as in 2D, but instead its has an
additional variable: Ax + By + Cz + D.
Furthermore, it's a plane in 3D instead of a line with a normal vector [A, B, C]. But as in 2D,
the normal vector is perpendicular to the plane Ax + By + Cz + D, and signed distance is the same with an added
variable const C.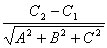 
Much like waves in 1D, the behavior of the waves stays relative the same in the 2D and 3D system.
The wavelength in 2D becomes a wavelength vector which is perpendicular to the level lines or the crests of the plane.
The wave length vector is a multiple of some vector [a, b]. So let the
constant multiple be k such that
= k [a, b]. Furthermore like the waves in 1D, the wavelength is the
distance between 2 crests, in the 2D case it becomes the signed distance ( ||||
) apart between 2 level lines or crests of the plane. So the signed distance
from level 0 to 2p
is:
Furthermore since
= k [a, b] and the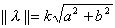 
then the constant k is 
. Therefore our wavelength vector
is 
Also our wave height changes as our wave equation changes.
Since our wave equation is related to the wave length, then as wavelength
changes into vector form, that means the wave equations must changes in some
proportion to it. The wave equation is now: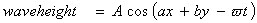 
where the [a, b] is related to ,
the wave length vector, t is the how the wave height changes with respect to
time, and is the radian
frequency which is the same in 1D. A visual representation at time = 0:
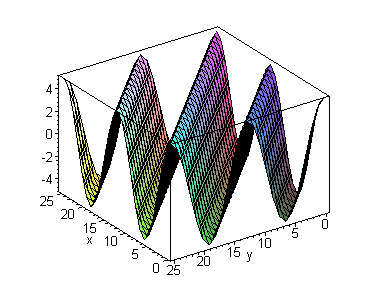
If you already notice from the previous sections that systems in
2D, are very similar in 3D, and that is the case for waves too. everything
has an additional variable since the vector increase by one variable ex. [a, b,
c]. So that means
= k [a, b, c] (the wave length vector is still a multiple of some vector but
now in 3D) the signed distance from level 0 to 2p
is: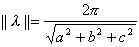 
and similarly the wavelength vector is: 
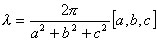and as well the wave height is: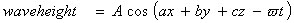
Course Web Page:
http://www.math.ubc.ca/people/faculty/cass/courses/m309-03a