Ax = constant
So x = constant/A

Consider the function Ax+By+C in 2-dimension, and set C=0 to start,
Draw the level lines Ax+By = constant
If B=0,
Ax = constant
So x = constant/A

If B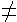 0,
0,
y = (const - Ax)/B
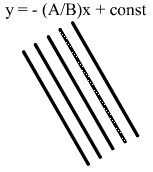
They are non-vertical lines.
We want a uniform way to describe the level lines of Ax+By without separating into cases B=0 and B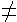 0.
0.
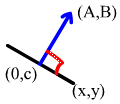
Ax+By=0
[A,B] * [x,y] = 0
[A,B]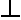 [x,y]
[x,y]