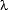= 2
/ (a^2 + b^2)^(1/2) and
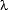is a multiple, k, of [a,b] Waves in 2-D and 3-D
Now that we have seen some properties of affine functions, we can understand wave motion in 2-D and 3-D with a little more ease.
Similar to the wave equation in 1-D, the wave motion is describe by an oscillating function "cosine", however there are a few more variables involve.
I will describe the case of 2 dimension in detail and explain the difference in 3 dimension later on.
Since we are in the 2 dimension space, we have to incorporate one more variable "y" to the wave equation.
The wave motion can be represented through level lines with each line being the crest of the wave. With the extra dimension, the wavelength is no long a value, it is a vector. So in order to calculate the wavelength, it is similar to calculating the distance between 2 level lines.
First we note that
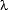= 2 / (a^2 + b^2)^(1/2) 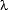is a multiple, k, of [a,b] So to calculate the wavelength or signed distance from a level line of 0 to 2, we do the following,
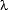|| = 2 / (a^2 + b^2)^(1/2) = k[a,b]
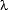/ (a^2 + b^2)
= (2 / (a^2 + b^2))[a,b]As for 3-D wave motion, just add another variable z and a constant c to the above equations.
So 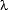becomes
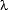= (2 / (a^2 + b^2 + c^2)^(1/2))[a,b,c]Similar to the wave equation in 1-D, when time = t is also a variable, the height of the wave in 2-D becomes a function of
t) where is the radian frequencyAs for wave in 3-D the height can be calculated with the following
t)By: Edmund Lai and Leo Cheng