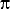 /
/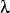 )x)
)x)Waves have the form
The (dimensionless) argument of the cosine function is called the "phase", and is of the form b (x - c t); we therefore see that it describes a wave which translates to the right (for positive c) in time. Let us take a more in-depth look at this wave equation.
A is the amplitude of the function, or light wave.
d is called the "phase angle", and effectively allows us to specify the relative "starting point" of the wave at time zero. By experimenting with various values of d (ie., 0, p / 2, p, 3 p / 2, 2p), we see that we can produce waves which have any given initial value (between - A and A) at time zero
Let us assume that if the amplitude is maximum at x = 0 this has the functional form:
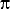 /
/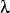 )x)
)x)Now, if this is moving to the right with speed v it will be described by:
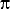 /
/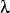 (x-vt))
(x-vt))So we see that a simple harmonic wave moving with speed v in the x direction is described as above. A plot is as follows:
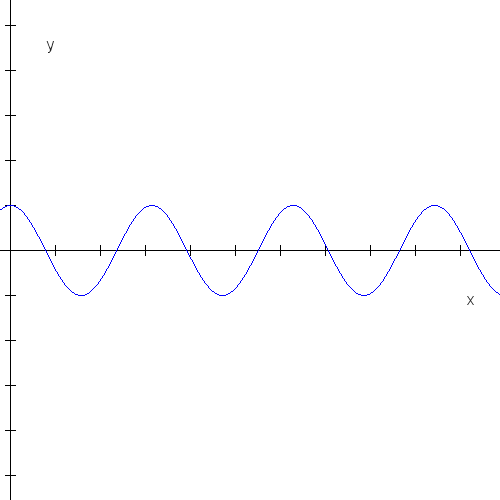
With c being the velocity and T as the period, by using c=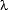 /T=
/T=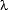
 /2
/2 as mentioned before, and by defining k=2
as mentioned before, and by defining k=2 /
/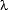 , we can write this as:
, we can write this as:
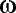 t)
t)F(x-ct) represents a wave of shape F(x) (at time t=0) moving in the direction of increasing x at constant speed c. That is, F(x-ct) represents the same shape as F(x), but with the origin moved to x=ct, ie the same shape as F(x) translated by ct units in the positive x direction.
F(x+ct) represents a wave of shape F(x) (at time t=0) moving in the direction of decreasing x at constant speed c. That is, F(x+ct) represents the same shape as F(x), but with the origin translated to x = -ct.
By: Edmund Lai and Leo Cheng