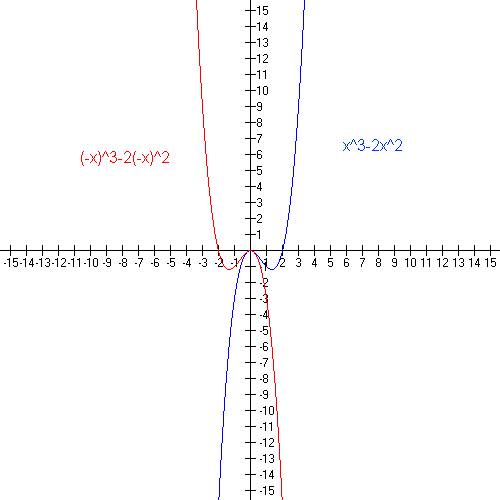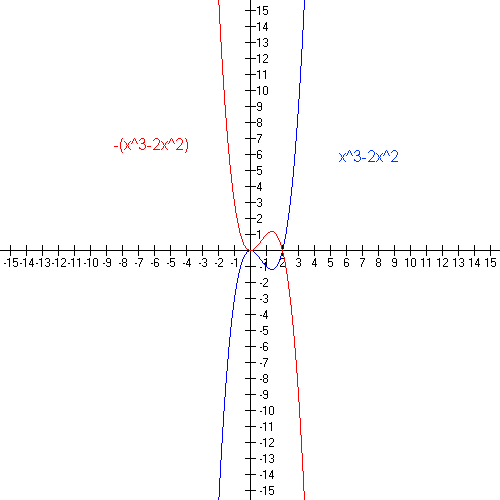In order to explain the dynamics of translating, compressing/stretching and reflecting a function, we start of with a common graph with the function y=f(x)=x^3-2x^2 as shown below. We will refer the function as the ORIGINAL FUNCTION.

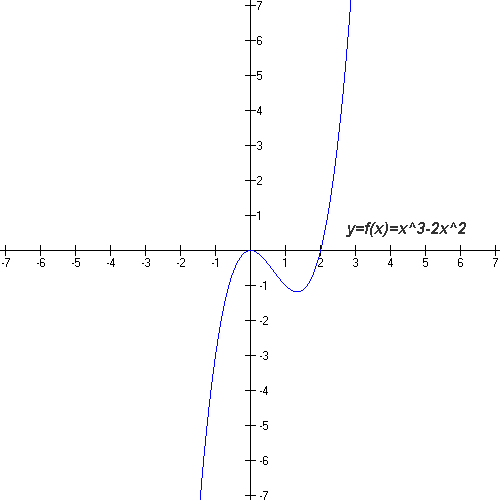
From here on, the BLUE will represent the orginal function while the RED will represent the function after being applied with c.

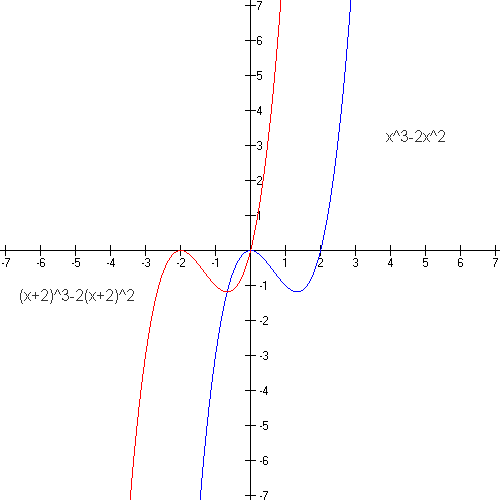
Translations of Functions. Suppose that y = f(x) is a function and c > 0; then

• the graph of y = f(x - c) is obtained by translating the graph of y = f(x) c units to the right; In this plot, 2 is subtracted from all x values. The function f(x-2) is obtained by substituting x-2 for x.
  

• the graph of y = f(x + c) is obtained by translating the graph of y = f(x) c units to the left; In this plot, 2 is added to all x values. The function f(x+2) is obtained by substituting x+2 for x.
  

• the graph of y = f(x) + c is obtained by translating the graph of y = f(x) c units upwards; In this plot, 3 is added to all y values.
  

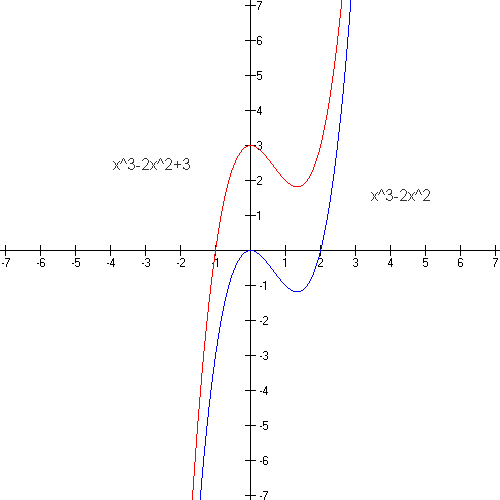
• the graph of y = f(x) - c is obtained by translating the graph of y = f(x) c units downwards. 3 is subtracted from all y values.
  

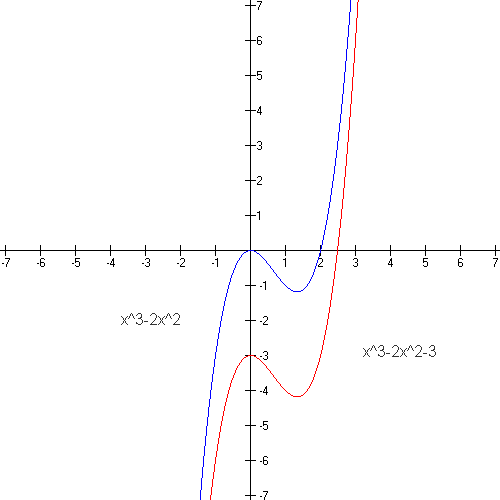
Compression and Stretching of Functions. Suppose that y = f(x) is a function and c > 1; then

• the graph of y = f(cx) is obtained by compressing horizontally the graph of y = f(x) by a factor of c units; In another word, the height at x on the new graph is equal to the height at 2x on the old one. The new graph is obtained by compressing the old one horizontally by 2. In substituting cx for x, horizontal distances are scaled by 1/c.
  

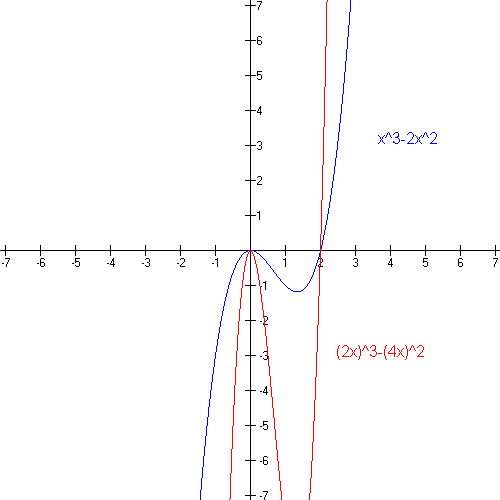
• the graph of y = f(x/c) is obtained by stretching horizontally the graph of y = f(x) by a factor of c units; In another word, the height at x on the new graph is equal to the height at (1/2)x on the old one. The new graph is obtained by stretching the old one horizontally by 2. In substituting x/c for x, horizontal distances are scaled by 1/c.
  

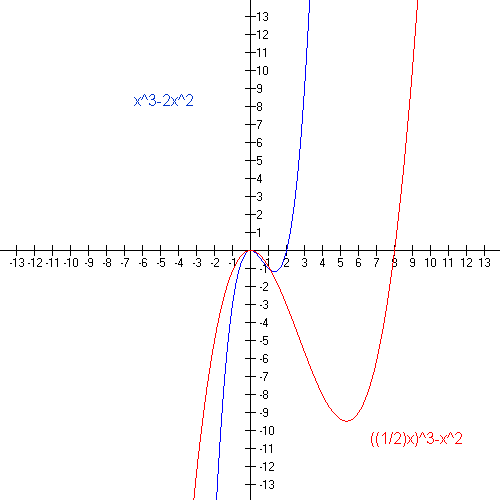
• the graph of y = cf(x) is obtained by stretching vertically the graph of y = f(x) by a factor of c units; In another words, from the function y = 2f(x), all y-values on the graph are scaled by 2. In subsituting cf for f, vertical distances are scaled by c.
  

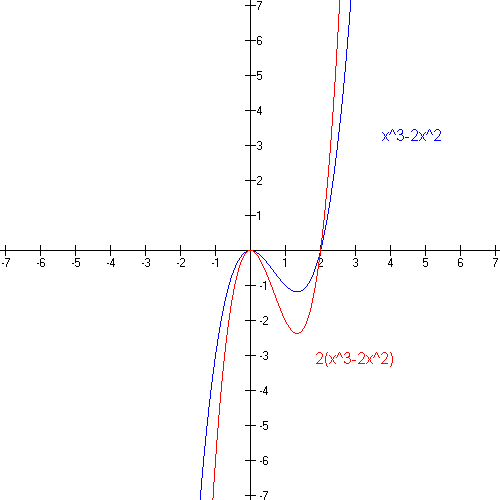
• the graph of y = (1/c)f(x) is obtained by compressing vertically the graph of y = f(x) by a factor of c units; In another words, from the function y = (1/2)f(x), all y-values on the graph are scaled by 2. In subsituting cf for f, vertical distances are scaled by 1/2.
  

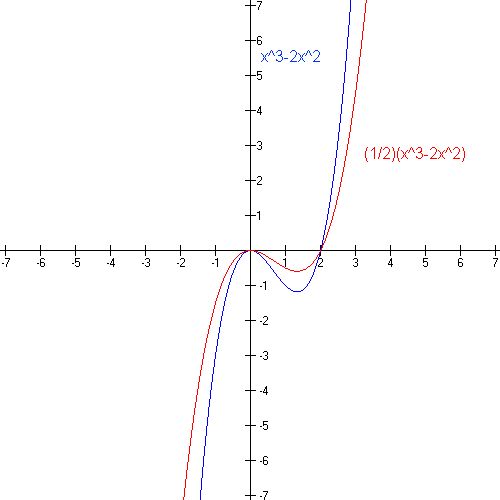
Reflections. Suppose that y = f(x) is a function; then

• the graph of y = f(-x) is obtained by reflecting the graph of y = f(x) across the y-axis;
  

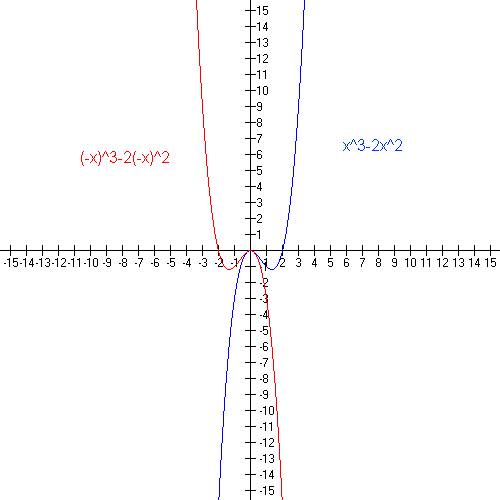
• the graph of y = -f(x) is obtained by reflecting the graph of y = f(x) across the x-axis;
  

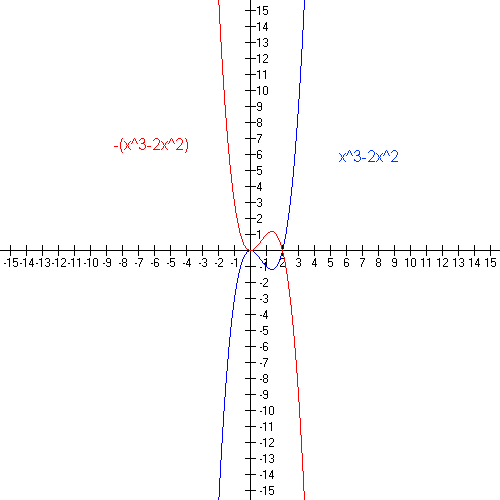
By: Edmund Lai and Leo Cheng