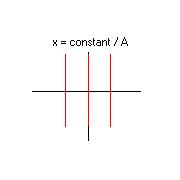
Note: Red = level lines
Affine Functions in 2D and 3D
To inspect the behaviour of a wave in 2 or 3 dimensions, we first need to understand some properties of an affine functions.
Definition: We say a fuction A(x) is affine if it is a combination of a linear function L(x) and a translation vector b.
An affine function with 2 variables has a general form of:
Ax + By = C where A,B,C are constants and x,y are variables
One way to view affine functions are by graphing the level lines of the function.
Definition: A level line is the curve where the function has a particular value.
There are two ways to visualize how the level lines look like, one approach is to consider 2 cases.
First case:
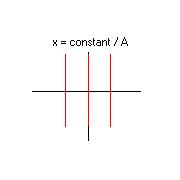 |
 |
Another approach is to find the orthogonal vector to the level line, in other words find the vector that is perpendicular to the level line.
Given the equation Ax + By = C,
If C = 0, Ax + By = 0. Since this is a linear combination, it can be broken into 2 vectors [A,B] . [x,y] = 0.
By the definition of orthogonal, [A,B] is perpendicular to [x,y].
If C not equal 0, Ax + By = C. But if we take 2 points (x,y) and (x',y'), we can subtract the two equations.
Ax + By = C
Ax' + By' = C
which will give A(x - x') + B(y - y') = 0, so [A,B] . [(x - x'),(y - y')] = 0 therefore [A,B] is still a perpendicular to some level line.
One might ask then what impact does the constant C have. In fact C is very important in determining the distance between two level lines.
Definition: Given two affine function Ax + By = C1 and Ax + By = C2, the signed distance between two level curve is given by dist. = (C2 - C1) / (A^2 + B^2)^(1/2)
Therefore it is easy to determine the distance of any level line to the line Ax + By = 0, simply take C1 to be 0. The equation is dist. = C / (A^2 + B^2)^(1/2)
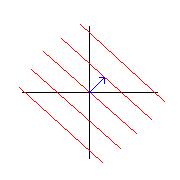
Note: Red = level lines and Blue = distance
As you will see, these properties of affine functions are important in Wave in 2D and 3D
By: Edmund Lai and Leo Cheng