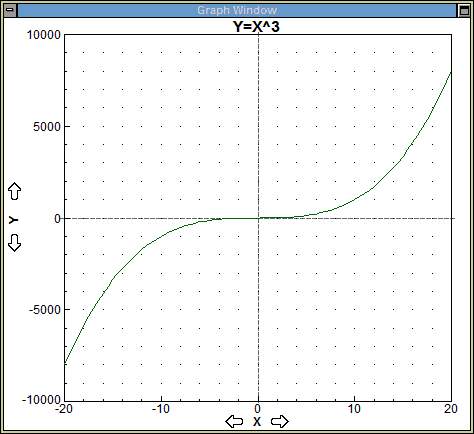
The way to understand elementary geometry of wave motion is to see what happens original graph y=f(x) becomees another graph y=af(bx+c)+d by scaling and shiting either x or y or both. The following graph in green color is f(x) and in other colors are scaled or shifted.

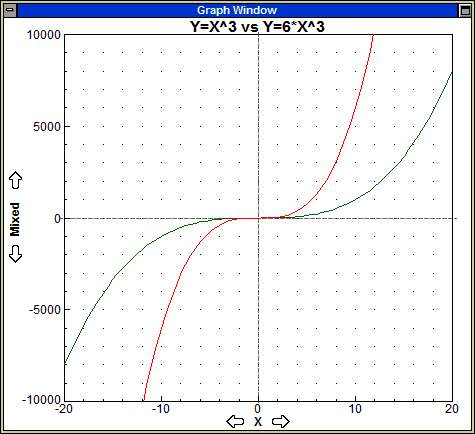
y = f(x)	y = 6f(x) Vertical distances are scaled by 6. The y-values on the graph are scaled by 6.
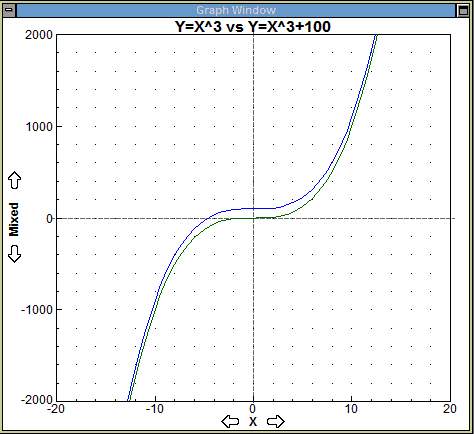
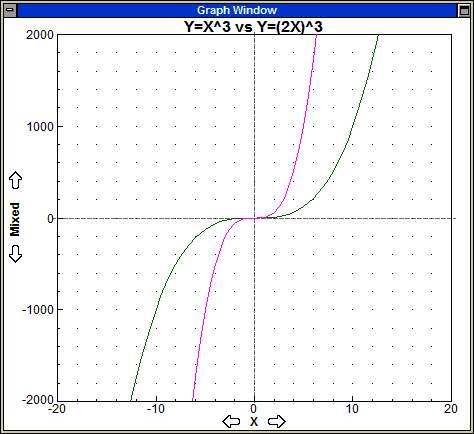
y = f(x) + 100 100 is add to all y-values.	y = f(2x) The new graph comes from compressing old graph horizontally by 2.
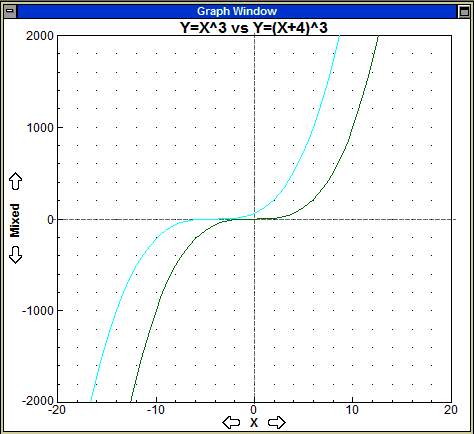
y = f(x+4) The graph is shifted left by 4.

We have show the 4 basic scale-and-shift method to modify the graph of f(x) in above.
The following is to illuste how to do with y = f(2x+4)+100.

• The function f(2x+4)+100 is obtained from f(2x+4) by adding 100.
• The function f(2x+4) is obtained from f(x+4) by substituting 2x for x.
• The function f(x+4) is obtained from f(x) by substituting x+4 for x.

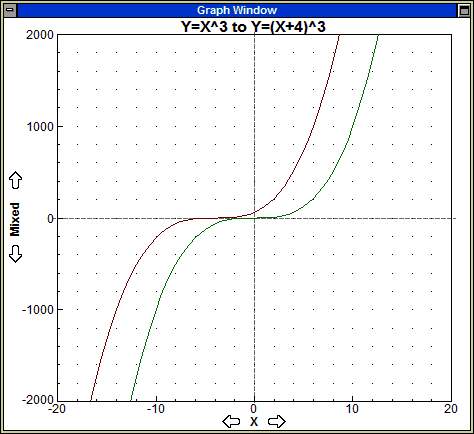• Substitute x+4 for x, y = f(x+4).
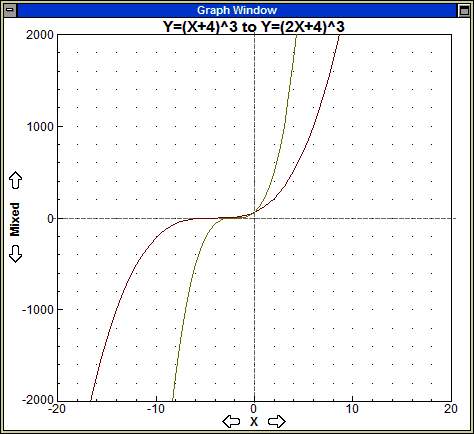• Substitute 2x for x, y = f(2x+4).
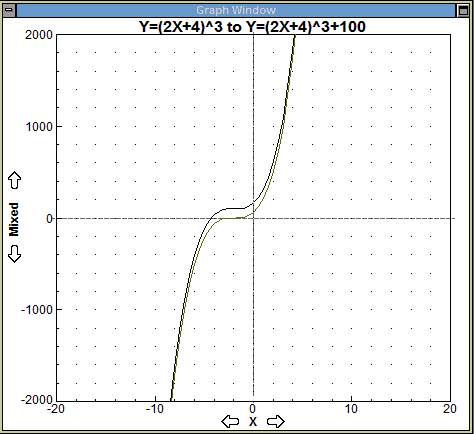• Add 100 to y, y = f(2x+4)+100.
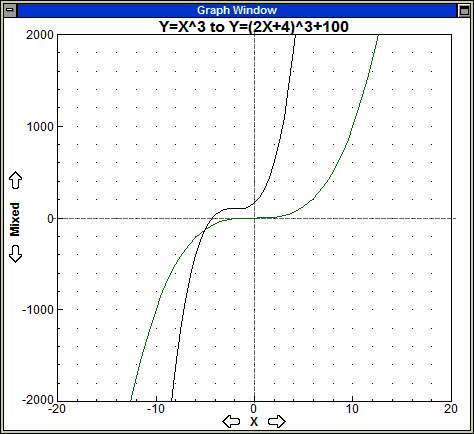• Now we have y = f(2x+4)+100 from y = f(x).