Julie Fun - Waves Page

Waves

Basic Parameters and Definitions
Fundamental Equations
Scaling and Shifting
Affine Equations
Waves in Several Dimensions

Basic Parameters and Definitions

A wave is a transfer of energy in the form of a disturbance, usually through a material substance or a medium.
All waves have a velocity, period, frequency, wavelength, and amplitude.

Velocity is the propagation speed of a wave and is denoted by the letter c.
Period is the time it takes to go through 1 cycle at a fixed point and is denoted by the letter T.
Frequency is the number of cycles completed in a unit of time.
In mathematics, we often use the radian frequency where the units are radians per second.
It is denoted by w, the Greek letter omega.
Wavelength is the distance between consecutive crests and is denoted by the Greek letter l, lambda.
Amplitude is the distance from the origin (equilibrium position) to the maximum displacement and is denoted by the letter A.

Fundamental Equations

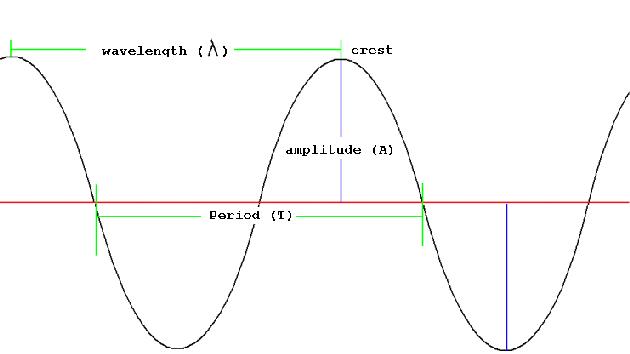
Fundamental Wave Equation
y = Acos(2p/l (x - ct))
or can be rewritten as:
= Acos((2px / l) - (2pct / l))

The relationship between frequency and period
T = 1/frequency = 1/(w/2p) = 2p/w

The relation between velocity, frequency, and wavelength
Any two of the above parameters will result in the third because:
c = lw/2p
substituting w = 2p/T, we get:
c = l/T

Scaling and Shifting

For the information on scaling and shifting functions refer to: Mathematics 309 - the elementary geometry of wave motion
Examples of shifting and scaling wave functions:

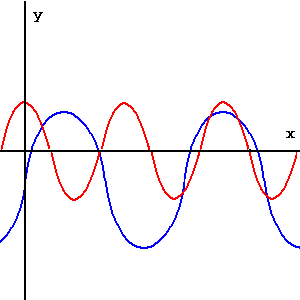
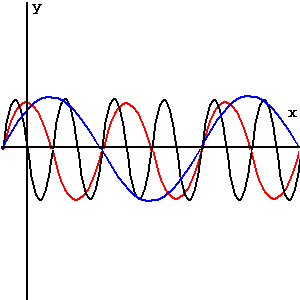Horizontal Scaling: changes in l y = cos(x) y = cos(.5x) y = cos(2x) Notice that an increase in wavelength = a decrease in the frequency and vice versa. Therefore it is possible to change the frequency instead of the wavelength when scaling horizontally	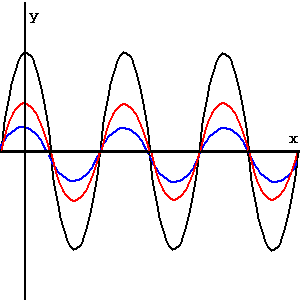Vertical Scaling: changes in A y = cos(x) y = 2cos(x) y = 1/2cos(x)
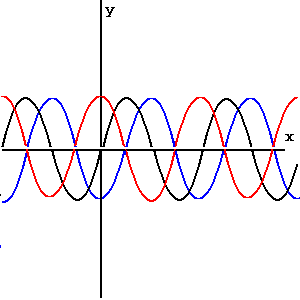Horizontal Shifting: Changes in c y = cos(x) y = cos(x - pt/2) y = cos(x + pt )	Vertical Shifting: adding a constant to the wave function y = cos(x) y = cos(x) - 2p y = cos(x) + p

Combining it all:

y = cos(x)
y = 1.5cos(x - p/2) - p/2

Affine Equations

Recall affine functions in 2D and 3D
in 2D: Ax + By + C an affine function of 2 variable
in 3D: Ax + By + Cz + d an affine function of 3 variables

Consider in 2D the function
Ax + By + C
to start set C = 0
then Ax + By = 0 is just the figure below

If C does not = 0, then we can rewrite the equation as:
y = (C - Ax) / B
this means that the level lines (a curve where a function has a single value) would not be vertical lines, in fact they would look like this:

We want a uniform way to describe the level lines of
Ax + By = 0
[A, B] . [x, y] = 0
means that they are orthogonal, [A, B] perpendicular to [x, y]
Furthermore, level lines of Ax + By are all perpendicular to [A, B].

Waves in Several Dimensions

What does affine equations have to do with Wave functions?
Notice that the wave height is just the equation: A cos(ax + by) where (a, b) is related to l, the wavelength vector.
How does it change with time? A cos(ax + by + ct) where ct = w, the radian frequency.

Page created by Julie Fun (worked individually) Math 309