Mathematics 309 - the elementary geometry of wave motion
Part I - Scaling and Shifting
Part II - Elementary Wave Functions (1D)
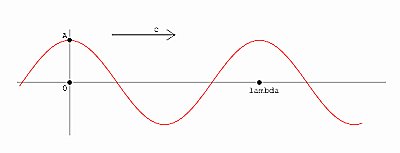
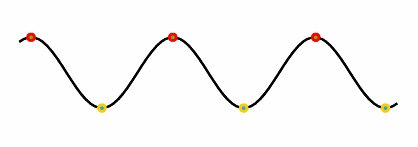
This is an example of simple periodic motion in one dimension (1D). The motion can be described using the parameters  , ,  , c, A, , c, A, 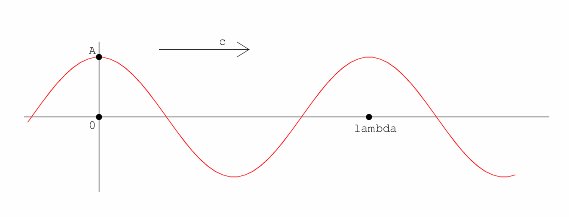
where 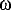 is the radial frequency (ie measured in radians per second, is the radial frequency (ie measured in radians per second, 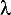 (lambda on the graph) is the wavelength which is the distance from one peak to the next, c the velocity (or speed in 1D) of the wave and A the amplitude or height of the wave. (lambda on the graph) is the wavelength which is the distance from one peak to the next, c the velocity (or speed in 1D) of the wave and A the amplitude or height of the wave.
A relationship can be found between these parameters using the basic equation of motion:
Speed = Distance/Time. For our case, the distance is
The wave equationThe picture above can be described with a mathematical equation. One can see the basic shape of the graph is a cosine wave. Using the methods of scaling and shifting described in part I the equation of a general wave function with unspecified parameters can be found.
A normal cosine wave has a period of 2 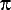 , but an equation is needed for any wavelength , but an equation is needed for any wavelength 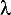 . Thus the third set of pictures shows the need to substitute 2 . Thus the third set of pictures shows the need to substitute 2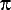 x/ x/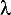 for x to get a horizontal scaling of for x to get a horizontal scaling of 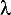 /2 /2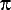 . Therefore the equation is more generally . Therefore the equation is more generally 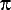 (x-ct)/ (x-ct)/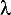 ) = cos(2 ) = cos(2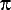 x/ x/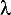 - 2 - 2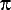 ct/ ct/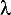 ) . ) .Next, variable amplitude A is needed instead of a unit amplitude. Similarly to the first set of diagrams in part I, the function is multiplied by a constant to get 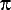 x/ x/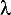 - 2 - 2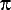 ct/ ct/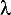 ) or, from above, y = Acos(2 ) or, from above, y = Acos(2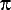 x/ x/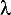 - - 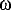 t). t).
Part III - Affine Functions and 2 and 3DNow waves in more than one dimension will be studied; the following diagrams illustrate a plane wave in 2D from two views; top and side. A 3D wave will have a velocity and wavelength acting in 3 dimensions, an example could be of waves radiating out from a sphere rather than a plane source. The wavelength and velocity in 2 and 3D will be vectors instead of scalars, to show the magnitude and direction of these parameters. It is known that the fundamental equation c =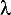 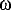 / 2 / 2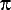 still applies, but in vector form. still applies, but in vector form.
Affine functions can be used to describe the wave height as a function of space and time. Recall that affine functions are transformations that preserve colinearity and the ratio of distances so that an object's intersection properties remain unchanged. The general form is Ax + By + Cz + D. A generalized formula for the height is y = Kcos(Ax + By + Cz + Dt), where K, A, B, C, D are constants to be determined. Obviously this is a case for 3D waves; 2D is just without the cz term. In this chapter 3D versions will usually be given; the 2D versions are similar, but again, without the z term.
If the general form of an affine equation above is taken, the constants can be identified: [A, B] (and similarly [B, C] and [A, C] in 3D) is the normal vector to the parallel lines. This is because
|
Sources:
|
MATH 309 Wave Motion |