Mathematics 309 - the elementary geometry of wave motion
Part I - Scaling and Shifting
One way of obtaining one graph from another is by scaling and shifting either x or y or both, so that the graph y=f(x) becomes the graphy = af(bx + c) + d. The way to see what happens to the graph is to understand what happens in simple steps with just one change at a time.

|
|
|
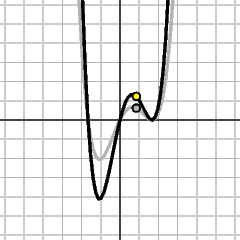
y = f(x)
|
y = 2f(x)
All y-values on the graph are scaled by 2. In substituting cf for f, vertical distances are scaled by c. |

|
|
|
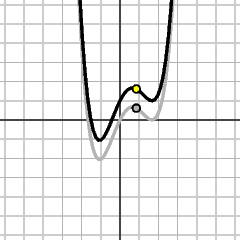
y = f(x)
|
y = f(x)+1
1 is added to all y values. |

|
|
|
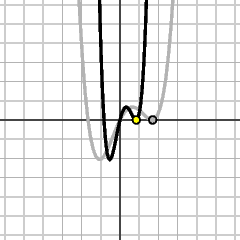
y = f(x)
|
y = f(2x)
The height at x on the new graph is equal to the height at 2x on the old one. The new graph is obtained by compressing the old one horizontally by 2. In substituting cx for x, horizontal distances are scaled by 1/c. |

|
|
|
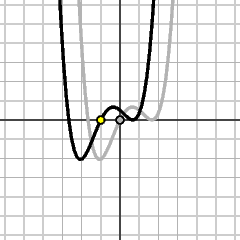
y = f(x)
|
y = f(x+1)
The height at x on the new graph is equal to the height at x+1 on the old one. The new graph is obtained by shifting the old one 1 to the left. |

|
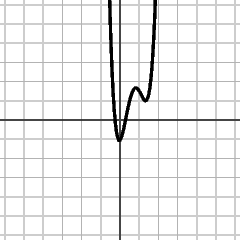
|
| y = f(x) | y = f(2x-1)+1 |
Only the last one is tricky, since it involves a sequence of substitutions. In order to see which ones, we unravel the process.
- The function f(2x-1)+1 is obtained from f(2x-1) by adding 1.
- The function f(2x-1) is obtained from f(x-1) by substituting 2x for x.
- The function f(x-1) is obtained from f(x) by substituting x-1 for x.
-
Substitute x-1
for x, y = f(x-1):
-
Substitute 2x
for x, y = f(2x-1):
-
Add 1 to y, y = f(2x-1)+1:
Part II - Wave Functions in 1D
a) Basic Parameters
The wave model of light pictures light travelling as a wave. Simple waves have the following basic parameters:- velocity = v = c (the speed of light) plus a given direction
- wavelength = λ
- frequency = ω
- amplitude = A
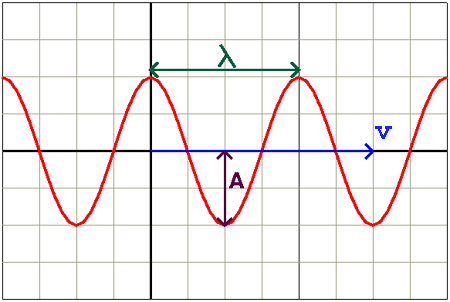
- The wave is travelling from left to right with a velocity (v).
- The wavelength (λ) is the distance between successive wave crests.
- There are 2 kinds of frequencies:
- 1) The number of wave crests which pass some point per second, expressed as cycles per second.
- 2) 2π multiplied by the number of wave crests which pass some point per second, expressed as radians per second.
- The amplitude (A) is the height of the wave, or half the vertical distance between the crest and the trough.
This is because T = period
= the time it takes to go through one cycle at a fixed point
= 1/frequency in cycles per second
= 1/(ω/2π)
= 2π/ω
In time T, the wave travels a distance λ.
Therefore, c=λ/T = (λω)/(2π)
b) Wave Equation
Recall the cosine function.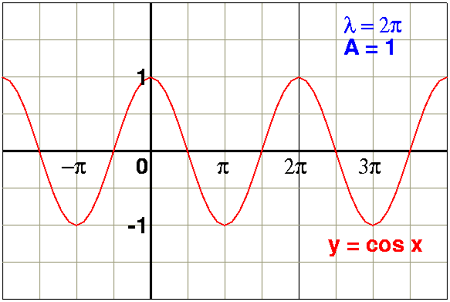
The equation for light waves in 1D can be obtained by scaling and shifting the cosine function.
We'll start with the cos function y = cos(x) and work our way, step by step, to the equation for light, y=Acos(2πx/λ-ωt)
STEP 1:
At time 0: y=cos(x) (wavelength = 2π)
At time t: the graph is shifted right by ct so y=cos(x-ct)
STEP 2:
Suppose the wavelength is λ instead of 2π.
Then we must scale the graph horizontally by λ/2π.
So y=cos(x) becomes y=cos(x/(λ/2π)) = cos((2πx)/λ)
And at time t, y=cos((2π/λ)(x-ct))
STEP 3:
We must scale the graph vertically to include the amplitude of the wave, A.
y=cos((2π/λ)(x-ct)) becomes y=Acos((2π/λ)(x-ct))
STEP 4:
Rearranging terms gives y=Acos((2π/λ)x-((2πc)/λ)t).
Recall that c=(λω)/(2π). Therefore, ω=(2πc)/λ, so we can plug ω into the wave equation.
Thus the finalized equation for light waves in 1D is:
-
y=Acos(2πx/λ-ωt)
Part III - Wave Functions in Several Dimensions
To understand the equation for the waveheight as a function of space and time we must first recall affine functions.
a) Affine Functions
An affine function is simply a linear function plus a translation (constant).The general equation is y=mx+c where c is the translation.
Extended to 2 and 3 variables the affine functions become ax+by+c and ax+by+cz+d respectively.
A level line is a curve where a function has a single value. We are interested in level lines because
the wavelength vector runs perpendicular to level lines,
therefore this concept is crucial in determining
the wave equation in higher dimensions. Using affine functions we can find equations for level lines.
In a familiar way, we can solve for level lines as follows:
Consider the 2D affine function 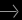 ax+by=const
ax+by=const
Using the fact that either b=0 or b≠0 we get two possibilities for the corresponding level lines:
- if b=0 the equation becomes
This is the equation for level lines that are vertical.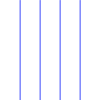
- if b≠0 the equation becomes
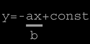
These level lines are non-vertical.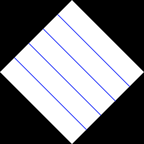
- if b≠0 the equation becomes
What if we wish to solve for level lines without breaking the equation into 2 separate cases?
Take ax+by=0
This can be rewritten in vector form as [a,b]•[x,y]=0
From the dot product, we know this must imply that [a,b] is perpendicular to [x,y]
ax+by=0 is the line through the origin perpendicular to [a,b]
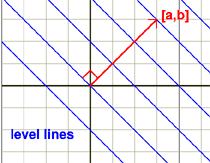
The level lines of ax+by are all perpendicular to [a,b]
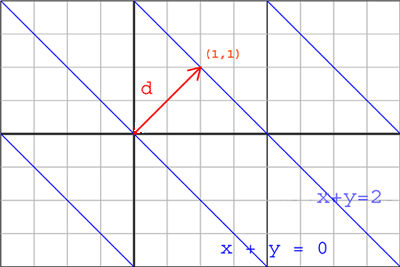
The signed distance (represented by d in the above diagram) between two lines, ax+by=c1 and ax+by=c2 is equal to
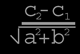
In the above example, signed distance=(2-0)/2^(1/2)=2^(1/2)
If the signed distance between two lines, ax+by=c1 and ax+by=c2, is positive, then the distance vector from ax+by=c1 to ax+by=c2 is in the same direction as [a,b]. If the signed distance is negative, then they are in opposite directions.
Now we can start to look at the wave equation.
b) Wave Equation in 2D and 3D
Again, we use the same parameters:
- c=velocity of the wave
- ω=radian frequency of the wave
- λ=wavelength vector
- A=amplitude
Let's first get an equation for λ, the wavelength vector.
Remember that the wavelength vector is perpendicular to level lines (wave crests). This implies
λ=multiple[a,b] in 2D or λ=multiple[a,b,c] in 3D
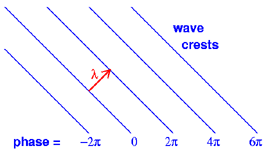 (Representation of waves in 2D)
(Representation of waves in 2D)
Using the signed distance from phase=0 to phase=2π we see that

Now, using the equation λ=k[a,b] or λ=k[a,b,c] we get

We now have 2 expression for ||λ|| (length of the wavelength vector). By equating the 2 expressions we get
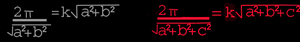
Solving for k:

Substituting this into our original equation λ=k[a,b] or λ=k[a,b,c] gives us our desired result
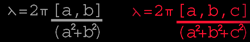
This leads us to our equation for waveheight.
At time t=0: waveheight=Acos(ax+by) waveheight=Acos(ax+by+cz)
Where ax+by+cz is the phase of the wave and A is the vertical scaling factor corresponding to the wave's amplitude.
To get this equation as a function of time, we use that at time t, the wave will have travelled a distance of ωt radians.
Thus, we must simply shift the graph to the right by ωt radians. We accomplish this in the following equation:
waveheight=Acos(ax+by-ωt) waveheight=Acos(ax+by+cz-ωt)
We have now derived our desired wave equations in 1D, 2D and 3D.
Katie Endersby, Stefanie Krzak, Amy Henderson