Part II - Basic Anatomy of the Wave & The Wave Equation
A wave is a periodic disturbance that travels through a medium. Each
particle in the medium oscillates back and forth but does not change position permanently.
In this way, energy is transfered from particle to particle through the medium.
Examples of waves:
-
A rope with one end tied to a post and the other being shaken by a person, creating
waves that travel along the rope.
-
Ripples on a pond after dropping a stone into the water. Notice that a previously stationary floating object will begin bobbing up and down but does not move in the direction of the wave.
-
Light. Light is special in that it can travel in the vacuum of space without a medium; thus it is not a wave according to the above definition. Nevertheless, light has many wavelike properties and it is often very useful to think of it as a wave.
We can model a wave, frozen at some particular time, as a graph with the following shape:
|
|

Figure 2.1
|
|
|
|
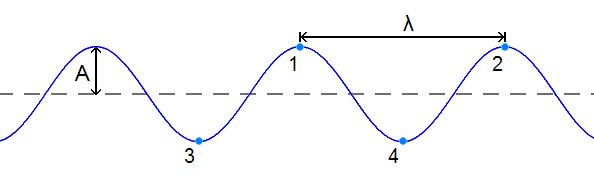
In this graph, the horizontal direction indicates position in the medium and the verticle direction indicates the displacement of particles (the amount of disturbance) at that position.
The dashed line drawn through the center of the diagram represents the equilibrium or rest position of the string. This is the position that the string would assume if there were no disturbance moving through it. Once a disturbance is introduced into the string, the particles of the string begin to vibrate upwards and downwards. At any given moment in time, a particle on the medium could be above or below the rest position. Points 1 and 2 on the diagram represent two of the crests of this wave. A crest of a wave is a point on the medium which exhibits the maximum amount of positive displacement from the rest positon. Points 3 and 4 on the diagram represent two of the troughs of this wave. A trough of a wave is a point on the medium which exhibits the maximum amount of negative displacement from the rest positon.
The wave shown above can be described by a variety of properties. One such property is amplitude. The amplitude of a wave refers to the magnitude of the displacement of a wave from a mean value. In our case, amplitude is simply the maximum amount of displacement of a particle on the rope from its rest position. We can also measure amplitude as the distance from the rest position to the trough position. In the diagram above, amplitude is represented by the letter A.
The wavelength is another property of a wave which is portrayed in the diagram above. The wavelength of a wave is simply the length of one complete wave cycle. A wave has a repeating pattern. And the length of one such repetition (known as a wave cylce) is the wavelength. The wavelength can be measured as the distance from crest to crest or from trough to trough. In fact, the wavelength of a wave can be measured as the distance from a point on a wave to the corresponding point on the next cycle of the wave. In a sine wave, the wavelength is the distance between peaks.
In the diagram above, the wavelength is the distance from 1 to 2, or the distance from 3 to 4. Any one of these distance measurements would suffice in determining the wavelength of this wave. Wavelength is commonly designated by the greek letter λ.
Suppose that a hand holding one end of the rope is moved back-and-forth two complete cycles in one second. The rate of the hand's motion would be 2 cycles/second. The first part of the rope, being attached to the hand, in turn would vibrate at a rate of 2 cycles/second. The second part, being attached to the first part, would vibrate at a rate of 2 cycles/second. In fact, the entire rope would vibrate at this rate of 2 cycles/second. This rate of 2 cycles/second is referred to as the frequency of the wave.
The frequency of a wave refers to how often the particles of the medium vibrate when a wave passes through the medium. In other words, frequency is the number of complete vibrational cycles of a medium per a given amount of time. Given this definition, it is reasonable that the quantity frequency would have units of cycles/second, waves/second, vibrations/second, or something/second. Another unit for frequency is the Hertz (abbreviated Hz) where 1 Hz is equivalent to 1 cycle/second. In our formulas, we will designate the symbol ω to mean frequency.
The speed of an object refers to how fast an object is moving and is usually expressed as the distance traveled per time of travel. For a wave, the speed is the distance traveled by a given point on the wave (such as a crest) in a given period of time. So while wave frequency refers to the number of cycles occurring per second, wave speed refers to the meters traveled per second. A wave can vibrate back and forth very frequently, yet have a small speed; and a wave can vibrate back and forth with a low frequency, yet have a high speed. We will use the letter c to signify speed.
Period refers to the time which it takes to do something. The period of a wave is the time for a particle on a medium to make one complete vibrational cycle. Period, being a time, is measured in units of time such as seconds, hours, days or years. We will refer to period using the letter T.
|
Relationships between properties
|
As you can imagine, some of the wave properties are related to one another and can be a possible source of confusion because of that. Out of those relationships however, we can extract some basic formulas that help us with our calculations.
- T = 1 / ω
Frequency and period are distinctly different, yet related, quantities. Frequency refers to how often something happens; period refers to the time it takes something to happen. Frequency is a rate quantity; period is a time quantity. Frequency is the cycles/second; period is the seconds/cycle. Hence, mathematically, the period is the reciprocal of the frequency and vice versa.
To take this calculation one step further, if we assume that the frequency we're dealing with is in radians/sec rather than cycles/sec, we divide the frequency by 2π to change it back into cycles/sec (because 1 cycle = 2Π radians) and hence ->
T = 1 / (ω/2Π) -> T = 2Π/ω
- λ = c/ω;
To get this equation we start from the fact that speed is equal to distance/time. That is ->
c = λ/T
Substituting equation 1 for T, we get ->
c = λω/2Π
Finally, converting from radians/sec to cycles/sec and solving for λ, we get equation 2. Another way to reason about this would be to notice that wavelength (length of a complete cycle) has an inverse relationship to frequency (cycles/sec), the number of peaks to pass a point in a given time. This makes intuitive sense since higher the frequency (number of cycles per sec), the smaller those cycles have to be in order to all fit in that amount of time (assuming constant speed c).
The wave equation can be derived in the following way:
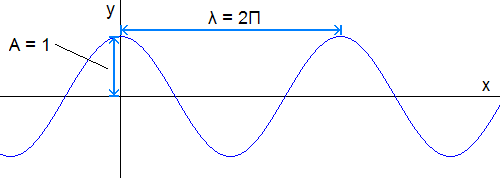
To model waves, we start with the equation y = cos(x). The cosine function has a wavelength of 2Π and an amplitude of 1 as the following figure indicates.
|
|

Figure 2.2
|
|
|
|
But we want to scale it horizontally to have any desired wavelength. To do this we must first scale by 1/2Π to reduce its wavelength to 1; then we scale by λ where λ is the desired wavelength. The combined effect of these two operations is to scale by λ/2Π. From Part I we know that scaling f(x) horizontally by a will transform the function into f(x/a). We can now write our function as:
y = cos(2Π/λ * x).
A wave is a function that moves in time. Recall from Part I that to displace any function f(x) to the right, you just change it's argument from x to x-a, where a is a positive number. If we let a = ct, where c is positive and t is time, then the displacement will increase with time. Hence cos(2Π/λ * (x - ct)) represents a forward propagating wave. Similarly cos(2Π/λ * (x + ct)) represents a backward propagating wave. Since c defines how much our wave is moved for each t, we can call c our speed. For simplicity, we will allow c to be negative as well as positive, so that we can describe waves moving in either direction using only the first formula. This new c is velocity since it expresses direction as well as speed. Our function so far is:
cos(2Π/λ * (x - ct))
Finally, we will take into account amplitude. Recall that the amplitude of a wave is the magnitude of its maximum displacement from a mean value. To increase the amplitude, we would draw our wave as having higher crests and lower troughs, or simply scale our equation vertically by some amount greater than 1. To scale a function f(x), we multiply it by some amount a (the amount we are scaling by) to get af(x). Since the amplitude of the equation we are starting with is 1, we need only scale it by the desired amplitude A. Applying this to our equation we get:
A * cos(2Π/λ * (x - ct)).
The resulting graph will look like:
|
|

Figure 2.3
|
|
|

|
