Meghan Cannon, Brenan Day
Mathematics 309 - the elementary geometry of wave motion
Part I - Scaling and Shifting 
One way of obtaining one graph from
another is by scaling and shifting either x or y or both, so
that the graph y = f(x) becomes the graph y = af(bx + c) + d.
The way to see what happens to the graph is to understand what happens in
simple steps with just one change at a time.
| y = f(x) |
y = 2f(x) All y-values on the graph are scaled by 2. In subsituting cf for f, vertical distances are scaled by c. |
| y = f(x) |
y = f(x)+1 1 is added to all y values. |
| y = f(x) |
y = f(2x) The height at x on the new graph is equal to the height at 2x on the old one. The new graph is obtained by compressing the old one horizontally by 2. In substituting cx for x, horizontal distances are scaled by 1/c. |
| y = f(x) |
y = f(x+1) The height at x on the new graph is equal to the height at x+1 on the old one. The new graph is obtained by shifting the old one 1 to the left. |
| y = f(x) | y = f(2x-1)+1 |
Only the last one is tricky, since it involves a sequence of substitutions. In order to see which ones, we unravel the process.
- The function f(2x-1)+1 is obtained from f(2x-1) by adding 1.
- The function f(2x-1) is obtained from f(x-1) by substituting 2x for x.
- The function f(x-1) is obtained from f(x) by substituting x-1 for x.
- Substitute x-1 for x, y = f(x-1):
- Substitute 2x for x, y = f(2x-1):
- Add 1 to y, y = f(2x-1)+1:
Part II - Wave Functions in 1D 
The two main types of waves are mechanical and electromagnetic. Mechanical waves are created through the disturbance of a medium, such as water or air, while electromagnetic waves do not need a medium, such as light, radio and x-rays,
We will focus on light waves and examine some of their major properties. A wave can be visualized by the graph y=cosx. Their basic parameters are velocity, frequency, wavelength and amplitude.
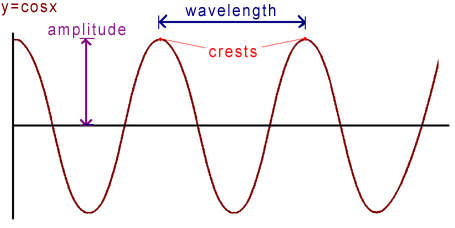
The highest point on the cosine graph, which represents maximum displacement, is called the crest.
Wavelength ( 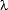 ) is the spacial distance between two crests (or the minimum distance of any two identical points on adjacent waves) of the wave. This is usually measured in meters.
) is the spacial distance between two crests (or the minimum distance of any two identical points on adjacent waves) of the wave. This is usually measured in meters.
Velocity ( c ) describes the speed of the wave. This is the distance a crest travels in a given time. c is measured in meters/second.
Frequency ( f ) is the number of wavelengths that pass a given point in a unit time. This is usually expressed in hertz = cycles/sec or radians/sec. We will be using angular frequency (  ) which we will simply refer to as "frequency" from this point on and it is used when measuring in radians. N.B.
) which we will simply refer to as "frequency" from this point on and it is used when measuring in radians. N.B.  = f (2
= f (2 ).
).
Amplitude ( A ) is half of the difference of the top and bottom peaks of the wave.
The period ( T ) is the time it takes the wave to travel one wavelength past a given point.
There are several equations that relate the above parameters:
- The period of y=cosx is 2
 , but the wavelength is now
, but the wavelength is now  so if we divide the original period by 2
so if we divide the original period by 2 (ie 2
(ie 2 /2
/2 = 1) then multiply it by
= 1) then multiply it by  (1
(1 =
= ) then we get the correct wavelength.
Thus, T = 1 / f = 1 / (
) then we get the correct wavelength.
Thus, T = 1 / f = 1 / ( / (2
/ (2 )) = 2
)) = 2 /
/  Thus we get the equation:
Thus we get the equation:
T=2
 /
/ 
- A commonly know equality is distance = velocity x time. Using wavelength as the distance gives the equation
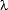 = cT. Rearranging this equation gives c =
= cT. Rearranging this equation gives c = 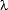 / T. Substituting T = 2
/ T. Substituting T = 2 /
/  in to this equation gives:
in to this equation gives:
c =
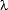
 / (2
/ (2 )
)
The wave equation
As described in Part I, functions can be scaled and shifted to form new graphs. The function y = cosx is widely used to portray a wave and can be altered to depict different wave characteristics.The wave equation is y=Acos[ (2
To understand how this "wave equation" works, it may be useful to formulate it from the original equation y=cosx. /
/ 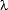 ) x -
) x -  t]
t]- The wavelength is no longer 2
 (which is the period of y=cosx) but
(which is the period of y=cosx) but 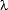 : y = cos[(2
: y = cos[(2 /
/ 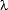 )x]
)x]
- At time t, the wave moves ct, so the graph moves ct to the right: y = cos[(2
 /
/ 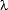 ) (x - ct)]
) (x - ct)]
-
The amplitude of the wave is A: y = Acos[(2
 /
/ 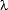 )(x - ct)]
)(x - ct)]
 /
/ 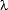 )(x - ct)] = Acos[(2
)(x - ct)] = Acos[(2 /
/ 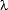 )x - (2
)x - (2 /
/ 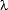 )ct)]. Since 2c
)ct)]. Since 2c /
/ 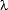 =
=  the equation can be rewritten as:
the equation can be rewritten as:
y = Acos[(2
 /
/ 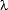 )x -
)x -  t]
t]
N.B. Some write the equation of the wave using the y=sinx instead of y=cosx which gives the same representation as long as the sine equation is shifted an extra /2 horizontally to the left.
Also, the wave number, k, can be substituted into the wave equation. k=2
/2 horizontally to the left.
Also, the wave number, k, can be substituted into the wave equation. k=2 /
/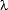 , thus the wave equation can also be written as y = Acos[kx -
, thus the wave equation can also be written as y = Acos[kx -  t]
t]
Part III - Affine Functions in 2D
A linear function, F(x), is a function that:
- preserves addition: L(x+y+z) = L(x) + L(y) + L(z), where x, y, z are vectors
- preserves multiplication: L(ax)=aL(x), where a is a constant and x,y,z are vectors.
An affine function is a function A(x) such that A(x, y, z) = a L(x, y, z) + b where a and b are constants and x, y, z are vectors.
The equation A(x)=aL(x) + b can be rewritten as a general solution y = mx + cMultidimensional affine functions:
A 2D affine function has the form Ax + By + C. In higher dimensions, the equation simply has more variable terms, i.e. a 3D affine function has equation Ax + By + Cz = D.
A level line is a curve where a function equals a constant.
For instance, the "curve" Ax + By = 0 has several important properties including:- It is the line through the origin perpendicular to [A, B].
- The dot product of [A B] and [x y] = 0 and are thus they are perpendicular
Similarly, we know the line Ax + By = C is perpendicular to [A B]. One important quality to notice is that this affine function is a multiple of 1 / [ (A^2 + B^2) ^ (1/2)] away from the line Ax + By = 0.
In fact, the distance between Ax + By = d and Ax + By = f, where d and f are constants, can be found with the formula:distance = [d - f] / [(A^2 + B^2)^ (1 / 2)]
- A commonly know equality is distance = velocity x time. Using wavelength as the distance gives the equation