ClaytonArnall - 74310996
Sukh Bajwa - 774422994
Mathematics 309 - the elementary geometry of wave motion
Part I - scaling and shifting
One way of obtaining one graph from another is by scaling and shifting either x or y or both, so that the graph y=f(x) becomes the graph y = af(bx + c) + d. The way to see what happens to the graph is to understand what happens in simple steps with just one change at a time.|
|
|
|
y = f(x)
|
y = 2f(x)
All y-values on the graph are scaled by 2. In subsituting cf for f, vertical distances are scaled by c. |
|
|
|
|
y = f(x)
|
y = f(x)+1
1 is added to all y values. |
|
|
|
|
y = f(x)
|
y = f(2x)
The height at x on the new graph is equal to the height at 2x on the old one. The new graph is obtained by compressing the old one horizontally by 2. In substituting cx for x, horizontal distances are scaled by 1/c. |
|
|
|
|
y = f(x)
|
y = f(x+1)
The height at x on the new graph is equal to the height at x+1 on the old one. The new graph is obtained by shifting the old one 1 to the left. |
|
|
|
| y = f(x) | y = f(2x-1)+1 |
Only the last one is tricky, since it involves a sequence of substitutions. In order to see which ones, we unravel the process.
- The function f(2x-1)+1 is obtained from f(2x-1) by adding 1.
- The function f(2x-1) is obtained from f(x-1) by substituting 2x for x.
- The function f(x-1) is obtained from f(x) by substituting x-1 for x.
-
Substitute x-1
for x, y = f(x-1):
-
Substitute 2x
for x, y = f(2x-1):
-
Add 1 to y, y = f(2x-1)+1:
Wave Functions in 1D
First, we will define the key terms used in simple periodic motion
Simple Periodic Motion - Motion that repeats itself. The motion that we will concern ourselves with assumes that the waves have constant velocity, period, frequency and wavelength.
Amplitude (A) - The maximum distance the crest of the wave travels from its equilibrium position.
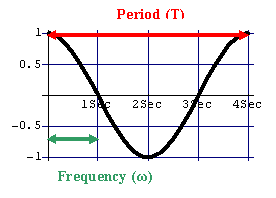
Period (T) - The time it takes for one complete cycle of the wave to pass by a fixed point. By one cycle, we mean one complete oscillation of the wave.
Wave Length (&lambda) - The spatial distance between two adjacent crests of the wave
Frequency) - The number of cycles per unit of time that pass a fixed point.
- Frequency and period have a reciprocal relationship; one is the inverse of the
other.
Example:
-
If the frequency is 2 cycles per second, then the period will be:
T = 1/ω
T = 1/2 seconds
- ω can also be measure in radians per second. To accomplish this change in
units(ie. scale), simply divide ω by 2π
As a result:
T = 1/(ω/2π)
T = 2π/ω
-
From simple physics, we know that velocity = distance/time. In our case, λ(wavelength)
represents the distance, c represents velocity, and T(period) represents time. Given any two
of these variables, the third can easily be determined. For example:
c = λ/T
c = λ/(2π/ω) = λω/2π

- What if we want to see what this graph looks like over a time t? Since λ = c*t, if we want to know the phase shift at time t, we shift it right by ct.
- y = cos(x - ct)

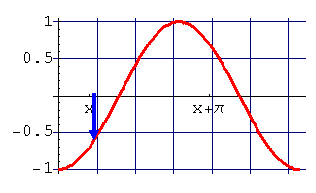
y = cos(x)
y = cos(x+π)
The height at x on the new graph
is equal to the height at x+π on the old one.
The new graph is obtained by shifting
the old one π to the left.- Up until now, we've assumed the wave has a wavelength of 2π. What if we want to scale the wavelength to something other than 2π? We have to adjust x in the function f(x)= cos(x) by a factor of λ/2π. That is:
y = cos(x)(λ/2π)) = cos(2πx/λ)

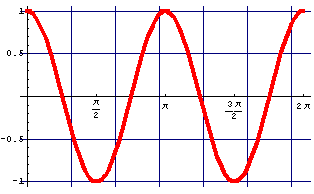
y = cos(x)
cos(2x)
The height at x on the new graph
is equal to the height at 2x
on the old one. The new graph is obtained
by compressing the old one horizontally by 2.
- If we combine this with the previous formula regarding the graph at time t, we will get the fundamental wave equation
-
y = Acos[(2π/λ)*(x - ct)], where A is the amplitude of the wave.
Wave Functions in Several Dimensions
- c = Velocity
- λ = "Wave Length" λ vector between crests.
- ω = time frequency
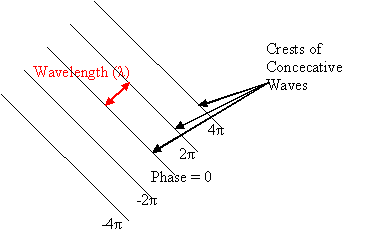
-
y = Acos(Ax + By - ct)
-
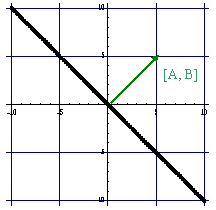
Ax + By + c = 0
-
Ax + By = 0
[A,B] • [x,y] = 0
[A,B]⊥[x,y]
The result of this is that the "curve" Ax + By = 0 is the line through the origin perpendicular to [A,B]
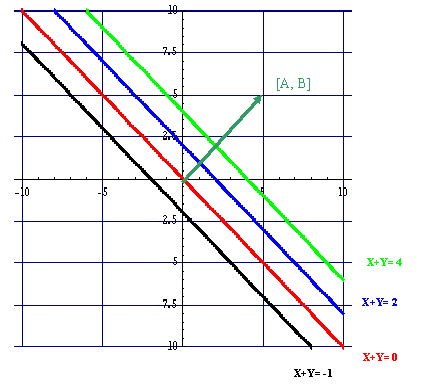
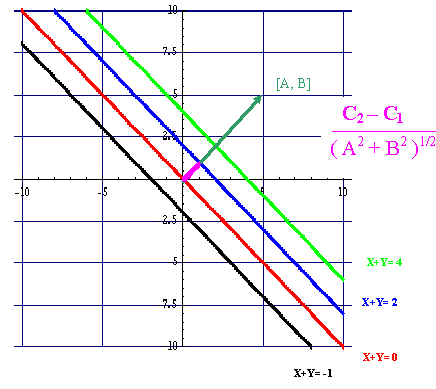
-
d = c/(sqrt(A² + B²))
-
d = (c2 - c1)/(sqrt(A² + B²))
-
λ = k * [A,B]
-
λ = k * (sqrt(A² + B²))
-
c/(sqrt(A² + B²))
-
λ =(c/(A² + B²))[A,B]
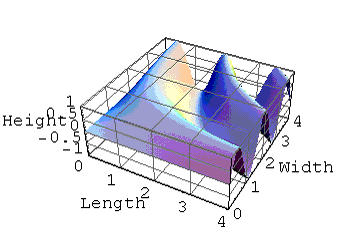
y = Sin(x) in 2D would become
z = Sin[xy] in 3D
 |
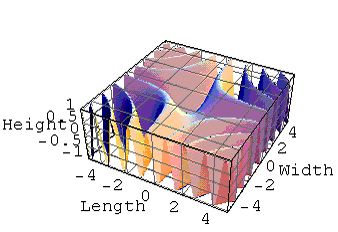 |
|
Sin[xy] in 3D for postive values of x and y |
Sin[xy] in 3D showing the saddle at the origin
|