Y Co-ordinate Changes: Scaling

Now we know how to raise and lower a graph by adjusting a constant; the graph keeps its shape and is moved up or down. The second type of change to a function's y values will change the graph's vertical shape. This are given the general form of y = c × f(x), where f(x) is the original function, and c is a constant value.

Let's take a look at two sample functions  to see how it works.


y = 2 × f (x)

1) Generate a Table of Values for y = 2 × x2



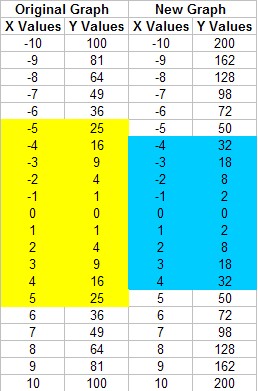
The values shown in yellow are used for the original graph. The values shown in blue are used for the new graph.

2) Plot the Graph of the Original Function and the New Function



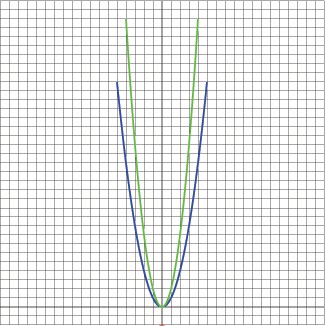
3) Compare the Graphs
The original graph is shown in blue, and the new graph is shown in green. How does it compare?

Be careful to notice that the green parabola doesn't have the same amount of data points as the blue one. If you compare the values around x = 0, ±1 , ±2 , or ±3 it appears that the new graph is twice the original graph. Its shape has changed, and it looks the somewhat taller.


y = 0.5 × f(x)

1) Generate a Table of Values for y = 0.5 × x2



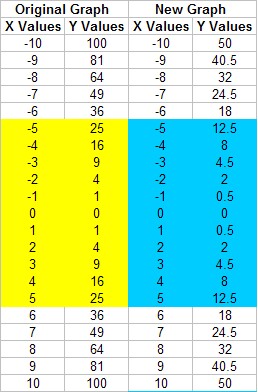
The values shown in yellow are used for the original graph. The values shown in blue are used for the new graph.

2) Plot the Graph of the Original Function and the New Function



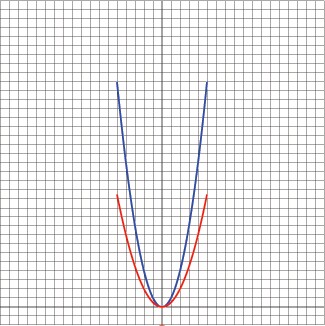
3) Compare the Graphs
The original graph is shown in blue, and the new graph is shown in red. How does it compare?

In this case, the red graph has the same number of data points as the blue one. It appears that the new graph is only half as high as the original graph. By comparing the table of values, this is more apparent. Its shape is different, but it looks like the original graph and is shorter.

The overall effect appears to be that multiplying a constant term to a function changes its shape. If the constant is greater than 1, the graph gets taller; if the constant is less than  1 the graph gets shorter. Result: y = c × f(x) is similar to y = f(x) but is either stretched (made taller) or compressed (made shorter).

Why does this happen?

When we evaluate the new function, we first evaluate f(x) at any value of x. In this case, the value of f(x) remains the same for that x value. Then by multiplying a constant term c, we scale the graph vertically by that factor. If c is larger than 1, each y value gets larger compared to the original value, but the x value stays the same. This gives the illusion the graph is getting taller or is stretched. If c is less than 1, each y value gets smaller compared to the original value, but the x value stays the same. This gives the illusion the graph is getting compressed and smaller. Multiplying with a constant factor, c, allows us to the change the vertical scale and look of a function.

On To X-Coordinate Translations
Back to Y-Coordinate Translations
Back to the Introduction