Composite Functions Using Translations -- Example #3

In this section, we will use what we know of translations to graph complex functions from simple ones. We will still use the y = x2 function, but we will apply multiple transformations all at the same time. The graphs following will show the transformations as they are applied one at a time. A greyed out graph shows the previous step and a blue graph shows the current step. Try to follow along as best you can.

General Principles
When you decompose a function and turn it into the sum of its translations, the best strategy is to work from the outside in. Start with the original function,and work with what is in the brackets, and then work outward. The first changes are always related to the x-coodinate; the y coodinate changes come last. The following examples should make it more clear. Dont' forget that f (x) = x2.

Graph of the Function 1.5 f (3x-6) +5
We again factor the middle in order to resolve the sequence of transformations.

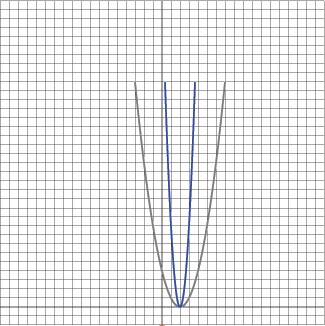
1.5 f (3x-6) +5 = 1.5 f [ 3(x-2) ] + 5

This means that the first transformation is of x-2. This results in shifting the graph right 2 units.
The second transformation involved the 3 coefficient inside the function. This results in a horizontal compression of 3 factors. The result should look like something on the right.
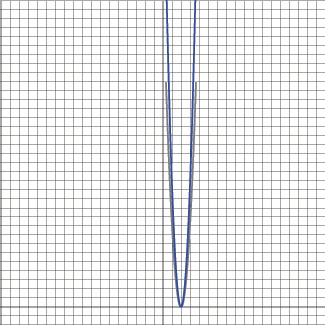
The third transformation is a constant scalar that lies outside of the function. We multiply all the y values by 1.5 to get the new function shape.
The last transformation comes from the + 5 that lies outside of the function. We add 5 to all the y values of the function, which is the same as shifting up the graph 5 units.

Many of the data points have left this graph's viewable region, so it may be difficult to tell the exact values of the graph currently.
This is a comparison between the original function and the new function. In this example, we use all four standard transformations.

These are the core tools that you'll need to understand basic function manipulation.

On to Wave Equations in 1 Dimension
Back to Composite Function Example Number 2
Back to the Introduction