Mathematics 309 - the elementary geometry of wave motion

Part III - The Wave Equation and Affine Functions



Now we move on to wave-functions in one dimension (and 2D and 3D later) The general equation is:

y = A * cos (x - wt)

However, to be more specific, the wave equation is:

y = A * cos ((2p/l)x - (2p/l)c)t)




Waves in Several Dimensions

c = velocity l = wavelength = vector between crests w = time frequency




Affine Functions


Affine functions ( in 2D and 3D ) are of the form:

Ax + Bx + C = ... ( of 2 variables )

Ax + Bx + Cz +D = ...( of 3 variables )


Let us consider the 2D function, and lets set C = 0.

Ax + Bx = 0


So what do these affine functions look like?

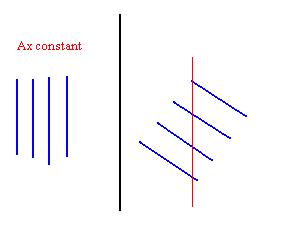In this picture, the level lines are the sloped lines on the right. On the left, these are the level lines if Ax = constant. The equation of the level lines on the right is y = -(A/B)x + constant.


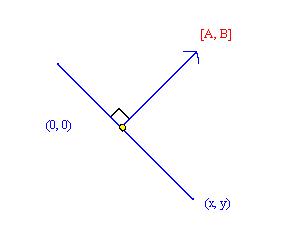
So we want a uniform way to describe the the level lines of Ax + By without separating the cases B=0, B=0. Using some vector analysis, we can do this.
Ax + By = 0
[A,B] * [x,y] = 0
[A,B] _|_ [x,y]
Therefore, a level line is a curve where a function has a single value.
The "curve" Ax + By = 0 is the line through the origin _|_ [A,B]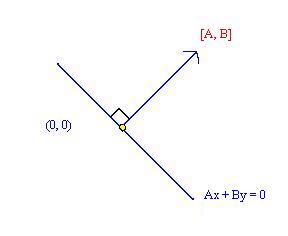

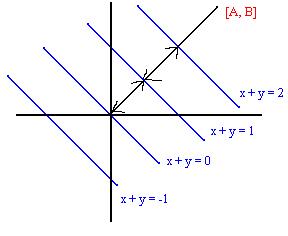More on level lines


The level lines of Ax + By are all perpendicular to [A,B], for example, look at the following picture:
In this example each line is separated by 1.

Now we move on to the general case of Ax + By = C. The line Ax + By = C _|_ [A,B] and at signed distance.

c / sqrt(A² + B²)

 from the line Ax + By = 0, c > 0 if the line is in the direction of [A,B].

For example, take the two equations:
Ax + By = c1

Ax + By = c2

Then the signed distance between them is:
c2 - c1 / sqrt(A² + B²)




Wave Motion in 2 Dimensions ( and 3D )

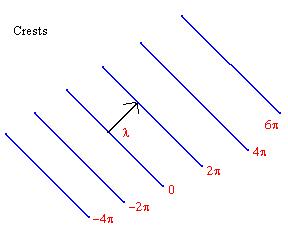y = A * cos(ax + by + cz) l = wavelength vector, perpendicular to the level lines.
l = a multiple of [a,b,c], the signed distance from level 0 to level 2p is equal to:

||l|| = 2p/sqrt(a² + b² + c²)



Note: the c in the equations listed here are for the 3 Dimensional equation, just eliminate any c for 2 Dimensional.

||l|| = 2p/sqrt(a² + b² + c²) = ksqrt(a² + b² + c²)

k = 2p/(a² + b² + c²) => l = 2p/(a² + b² + c²) * [a,b,c]




All images created with MSPaint by Alfred Chan 2003.