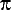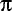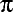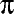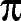Mathematics 309 - Spring 2003
Special. My office hours on Thursday, April 3, will be 10:00 - 12:00, 2:00-4:00.

From the title page of the Treatise on optics by Sir David Brewster (1853)
- Section 201
- Buchanan D339
- MWF 2:00
There is no required text, but several recommended reference texts (ones I use myself to prepare) are listed below. Much information is available on the Internet.
There will be a few unusual features of this class:
- I will write lecture notes occasionally, but the basic class notes are going to be provided by the class itself. I will divide the class into groups of roughly three students each. Each group will be responsible for recording and reproducing for the Internet exactly one class, based normally on my lecture. Very rarely, towards the end of the term, the group itself may be asked to produce the lecture. Each group will have a few tools, such as a digital camera and tape recorder, to record the class and a few hints about how to turn these into Web material, but in the end they must come up a complete written web page explaining the material for that class. There will be a deadline of one week to produce a preliminary version for class distribution, and another week to take criticism into account. Each of these pages will count 10% of a student's final grade, with bonuses awarded for really great stuff.
- Each student will be required to do an individual project of some kind at the end of the term.
In short, I am hoping to get an extremely high rate of active student participation.
There will be a small amount of instruction in techniques needed to post mathematics on the Internet. This will involve an introduction to very basic PostScript programming as well as a brief introduction to html and Web image production. Students who have taken my section of Mathematics 308 will be at a slight advantage, but this edge should disappear rapidly.
Emphasis will be placed on the use of graphics to illustrate mathematics.
For viewing many illustrations in this course, as well as for other purposes, you will need to install GhostScript/GhostView on your computer. For many tasks you will also find it convenient to have a simple image manipulation program, such as one of the simplified versions of PhotoShop, on your machine. You should also be able to log into the Mathematics Department machines from remote locations.
Topics
-
Introduction
- Wave motion in 1D
- Linear functions in 2D and 3D
- Simple wave motion in 2D and 3D
- Refraction of waves
- Waves and rays
- Gaussian optics
- Fermat's principle
- Linear optics
- Aberrations
- Interference and diffraction
- Gaussian integrals
- Fresnel's theory
- Holograms
- Polarization
- Rainbows and other meteorological optics
The classes
- Elementary geometry of waves
- Rays or waves? (Introduction)
References
- Victor Guillemin and Shlomo Sternberg, Symplectic techniques in physics, Cambridge University Press, 1996. The only relevant chapter is the first, which is great mathematical writing. (The same cannot be said of the rest of the book, alas.) This covers essentially the same material as this course, although not at the same level.
- A. Gerrard and J. M. Burch, Introduction to matrix optics, Dover, 1975. This is not a very exciting book, but has a number of useful ideas.
- R. P. Feynman, Lectures on Physics, volume I. This is an advanced first year physics text. Chapters 27-30 and 33 are relevant here.
- William Rowan Hamilton's home page (!) including the text of much of his work. David Wilkins' pages contain other valuable mathematical classics as well.
- Optic 2001 lists all kinds of stuff, of wildly varying quality.
- Rudolf Kingslake, Lenses in photography, A. S. Barnes, New York, 1963. The author was at the time director of optical design at Eastman Kodak.
- Leonard Taylor's capsule biographies
- JML Optical - on ray tracing
- Indices of refraction - a table of values for many substances
Web pages on various things
- The first topic. This page includes a link to a .zip file which will allow you to load onto your own machine the collection of images and text that makes it up. In order to unpack this .zip file you will need the shareware program WinZip. There are several places on the Internet from which you can obtain it. Try entering "Winzip download" in google.
-
Here is a zip
file of images of
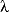 s,
s,
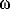 s, and
s, and  s (Greek letters)
in different sizes.
s (Greek letters)
in different sizes.
-
-
Sources of information on material in the first week or so
in this class, some of which you might
find helpful for your own work, can be found by entering
"frequency wavelength velocity" in google. You will
get thousands of references, about the same
number as if you enter "Adam Sandler punchdrunk love."
Hard to believe, but waves are a hot topic.
-
Projects will be graded on the basis of:
- mathematical content (how much mathematics is involved? how relevant to the course material?)
- clarity (arguments will ideally be transparent, and context explained; graphics must be easy to read, aimed at mathematics; well designed to convey ideas rather than distract)
- correctness (no serious mathematical errors)
- difficulty (how much work involved, and how much technical knowledge?)
- interest (as interesting as possible, given the topic)
- originality (how many of the ideas and how much of the execution are yours?)
- technical skill (are ideas presented graphically where possible? text well written?)
-
There are lots of tools available for image manipulation
and other useful tasks
on the Mathematics Department machines, and if you can connect to
one of our machines, you can use them
at home almost as easily as if you
were in the building. There are two
programs you will need to install on
your computer
if you are running Windows.
One is ssh, a program
that sets up connections oner the Internet. The other is
something that runs X windows.
A version of ssh that costs nothing and that, according to one member of our class, works very well can be downloaded from PuTTY.
As for X11, try Cygwin.
If you try these out, I'd be interested in knowing how you find them.
-
One useful tool for image manipulation is GIMP.
Until recently it was available
only on UNIX systems,
but now it is OK for Windows as well. Check
out the GIMP home page.
If you want to change PostScript files to .jpg files (or .gif
files if you have that GIMP plugin),
you must have the PostScript interpreter ghostscript
on your system. And, apparently, there must be a copy of
the file gswin32c.exe in the directory C:\windows.
- Course notes
- Assignment 1
- Assignment 2
- Assignment #2 - grades
- Assignment 3
- Assignment 4
-
The second mid-term will be Friday, March 21.
- Solutions to this mid-term
-
Assignment 5
- One student's perfect answers to this assignment
- The project - ground rules
-
Suggested topics
-
Waves and light.
I had originally hoped to say more about
this in class, but in fact the only thing
we have examined in class is
that refraction
is best explained as a consequence of waves
traveling slower in denser media. There are many
other topics to be explored at
a level not too difficult:
(1) Why light seems to travel in a straight line through wide slits, and why it doesn't do so through narrow slits.
(2) The extra (`supernumerary') bows in a rainbow, or the `true' rainbow theory due to G. B. Airy.
(3) The limits of resolution in light microscopes and the effect of the width of a lens system on its properties.
All of these involve interference of waves. - The way real optical systems such as binoculars, eyes and eye-glasses (most interesting is astigmatism), cameras (particularly zoom lenses), astronomical telescopes, and microscopes are built, and why. Possible topics here involve chromatic aberration (and how it is fixed), pincushion and barrel distortion, what zoom lenses do as they are adjusted, depth of field in cameras. These would involve mostly complicated ray tracing.
- Classical optics in terms of matrices. What are the principal planes of an optical system? the true focal length? Why are these concepts useful?
- Simulated imaging in terms of pixels and discrete distributions of ray directions to tie the ray theory to real questions of visibility.
- More complicated kinds of non-linearity (lens aberrations other than chromatic).
- Fermat's principle that light rays minimize optical length.
- Atmospheric refraction - why stars twinkle, why the sun is actually below the horizon when it sets.
-
Waves and light.
I had originally hoped to say more about
this in class, but in fact the only thing
we have examined in class is
that refraction
is best explained as a consequence of waves
traveling slower in denser media. There are many
other topics to be explored at
a level not too difficult:
-
I have taken the following books from the UBC library to
make available to the class for perusal:
- Geometrical optics, J. P. Southall (1913)
- Mirrors, prisms, and lenses, J. P. Southall (1918)
- Elementary geometrical optics, A. S. Ramsey (1920)
- Geometrical optics, H. G. Zimmer (1970). This is distinguished by the remark "Numerical calculations are not popular because they require considerable self-discipline." This was written before lens designers used computers extensively.
- The projects themselves