Lines Normal to the Ellipse

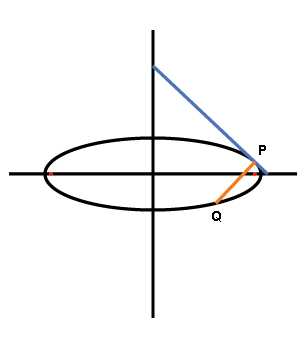
Let a and b be the semi major and minor axis of the ellipse given by

     y = ±b(1 - (x/a)²)^1/2

Given any point P on the ellipse (consider, without loss of generality the 1^st quadrant), draw the normal
to the tangent at P, and call the intersection with the opposite side of the ellipse Q.

What is the minimum PQ, or the shortest normal chord of the ellipse?

In Japanese Temple Geometry (Scientific American, May 1998) article by Tony Rothman, a solution is given by minimizing a function for the length of PQ.

http://www.sciam.com/1998/0598issue/0598rothman_ans3.html

This result, however, is very unsatisfactory, and leads us to ask the following question:

Where must the shortest normal chord PQ be located?

As a starting point, consider the trivial case of the circle.

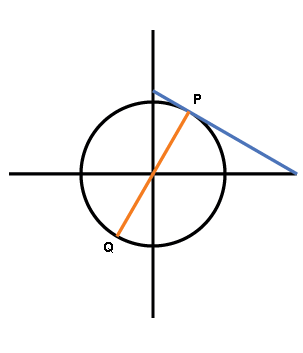
The solution here is a familiar one: Every normal to the circle passes through the centre, and hence the shortest normal chord is simply the diameter.

The question becomes more interesting as the eccentricity of the ellipse increases. In the following examples, the bar on the left indicates the length of the normal chord with respect to the semi minor axis, b.

Example 1
Example 2

Next, we make the ellipses even less circular, and the minimum normal chord length is indicated in yellow.

Example 3
Example 4

From these examples, it would appear that the shortest normal chord is at least 2b in each case. Examples 3 and 4 show us that in some cases, the length is certainly less than 2b. The minimum in these cases is calculated using Rothman's result:

     27^1/2a²b²/(a²+b²)^3/2

However, this formula is only defined for 2b² < a².

This is one of many curious facts about this problem. What happens for 2b² > a²?

Notice that we are in fact defining a map between points on the ellipse. For each point P on the ellipse, the normal at P gives us a point Q on the opposite side of the curve. What is important is that Q = Q(P) is completely determined by P. Or, if x is the the x-value of some point P on the ellipse, then Q(x) is the corresponding x-value for Q(P) and can be found, as it is in the animations, using the quadratic formula.

In examples 3 and 4, the normal chords drift right towards the minimum, and then turn around. So, as x moves from 0 to a, Q(x) moves to the right to some value 0<t < a, and then turns around. In these cases, the map is 2-to-1 on the interval (0, t). This means that in this interval there are points P and P' for which

     Q(P) = Q(P')

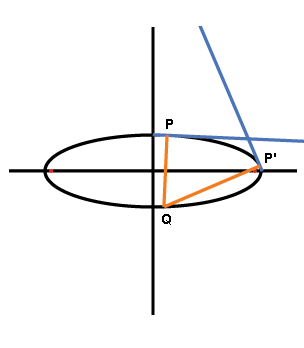
However, given P and Q, it is difficult to find P'. The result is a messy polynomial of degree 4, which even Maple complains about.

From examples 3 and 4, it would seem that the shortest normal chord corresponds to this maximum (in the x-sense) value for Q, or the point at which the chords head back in the opposite direction.

A second interesting point is the point P (other than (0,b)) which maps to Q = (0,-b).

This is simply the y-intercept of the normal line for some point P. It turns out that this P on the curve is given by

     x = a²(a²-b²)^1/2/(a²-b²)

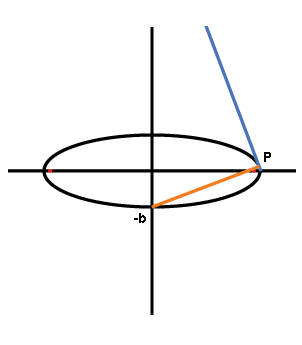
Notice that x is not defined for 2b² > a². However, this inequality is familiar. It is similar to the restriction given by Rothman's formula. In fact, we now have a division of ellipses in to two categories:

     2b² < a²       (1)
     2b² >= a²     (2)

Example 2 is the case where 2b² = a².

Ellipse of type (2) all have a 1-to-1 map from points on the ellipse in the 1^st quadrant to points in the 3^rd, and no 2-to-1 part. Further, these ellipses seem to have a minimum normal chord length of 2b.

We have the following observations:

• type (1):
  Minimum PQ given by Rothman's formula, the location of which appears to be the largest Q(x) for some x in (0, a).
• type (2):
  Minimum PQ is appears to be 2b the minor axis itself.

But why is this? And how can we show that this is in fact the case?

Here is my best attempt....

In the following figure, all of the triangles in the are similar:

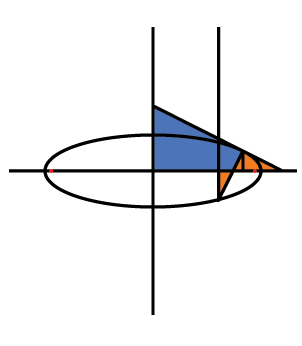
In particular, the orange triangle and the triangle composed of the 3 blue line segments are similar:

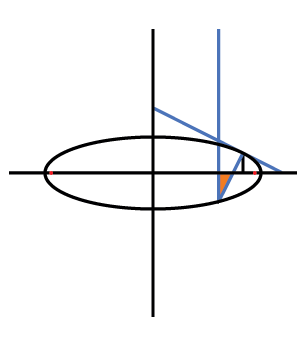
Here is a closer look at this figure:

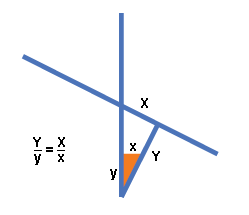
By similarity, the length PQ that we are intersect in is

     Y = X(y/x)

Consider the following animation:

Example for a type (1) ellipse

Example for a type (2) ellipse

In both cases, the goal is to make the number X(y/x) as small as possible. Ideally, we would make Xy small and x large. However, x, y and X all very in different ways.

The type (2) ellipses are a little easier.

We observed that the map from P to Q in this case is 1-to-1. x increases monotonically from 0 to a. y decreases monotonically from =<b to 0. Further X is increasing, as in the example, to infinity. So it seems reasonable to chose the minor axis as the smallest normal chord.

The type (1) ellipses are more complicated.

We would like to say that as y is proportional to Y, it makes sense to choose the smallest y possible to minimize Y. This in fact agrees with the intuition developed through examples, however, we must consider the effects of X/x also. Returning to the example, notice that initially, both x and X increase slowly since the left most blue line moves with them. Simultaneously, y is decreasing. It is after y begins to increase again that x and X begin to increase at a higher rate. With this in mind, it does seem as though the point at which y is smallest (or Q(x) largest) corresponds to the smallest normal chord.

This is still less than a completely geometric proof. However, it does illustrate the difficulty of finding such a solution, and how dynamic such a system is.

This document can be found online at: http://fynn.com/liam/309/index.html

Last updated 04/26/01, 7:14pm   liam@lineski.com