Circular Orbit
Elliptical Orbit
Near Earth Orbiting Satellites
There are many satellites orbiting Earth. They are used by the military, telecommunication companies as well as by the scientific community.
There are two broad categories of orbiting satellites: low orbit and high orbit satellites. Low orbit satellites are close to the earth's surface and can therefore take detailed pictures of the surface. They are about 100-1000 N.M. (1 nautical mile = 1852 metres) above the surface of the earth. The military uses this for reconnaissance purposes. Other uses include terrain surveying which can be used by forest companies to plan their harvests.
High orbit satellites are more than 5000 N.M. above the surface of the earth. At this altitude, atmospheric drag is removed and the satellite has a direct line of sight with a large portion of the earth. It is too far for detailed photography but the vast line of sight makes it ideal for communication satellites. This allows a satellite to transmit and receive data to and from many points on earth at any given time. This reduces the number of satellites required for a functional communications satellite network.
I want to discuss the physics of moving satellites between low and high orbits. This might be needed because the satellite was to be launched in two stages: launch from earth into a low orbit and then it is moved into a high orbit. Or the nature of use of the satellite might change requiring a different altitude for the satellite.
General Orbits
Satellites follow an elliptical orbit around the earth. Circular orbits are simply special cases of elliptical orbits.
|
Circular Orbit |
 |
Elliptical Orbit |
 |
There are certain characteristics of an ellipse that are needed for understanding orbits. An ellipse has 2 focii points that lie along the semi-major axis. The focii, F1 and F2, are defined such that the distance from F1 to a point A on the ellipse to F2 is constant for any A.
The semi-major axis has length 2a. We define the closest point on the ellipse to F1 as the perigee (this point lies along the semi-major axis). This distance is called the perigee distance. We define the apogee as the opposite point along the semi-major axis.
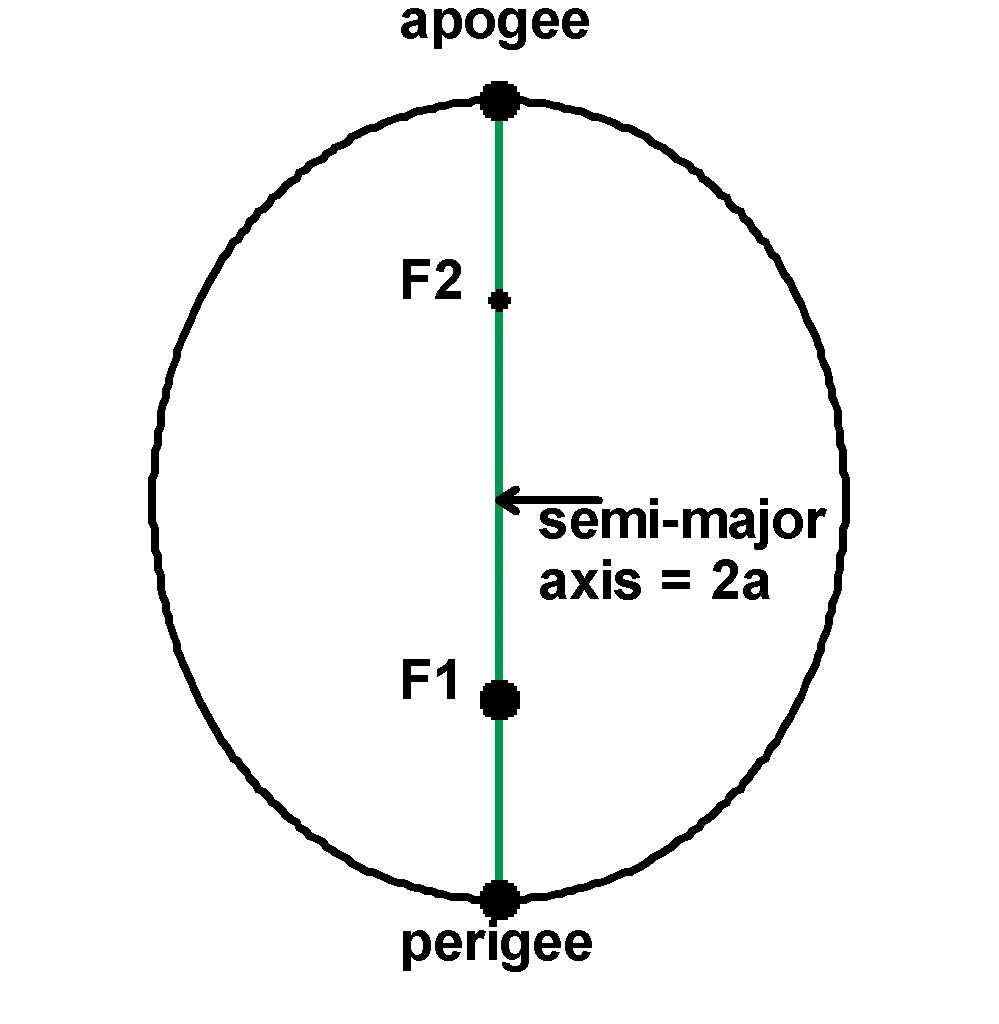 |
By Newton's Second Law we know how two bodies attract each other.
We will apply this Law to our satellite and earth. However, we will make simplifying assumptions. We will ignore attractions from the moon, other planets and the sun. We will only consider the acceleration on the satellite due to the earth. Even with this simplifying assumption our equations are still relatively accurate. The relative accelerations can be viewed here.
We will also ignore atmospheric friction, earth oblateness and assume that the earth has uniform density.
This gives us the two-body problem:
| a = G(M+m)r / r3 ~ GMr / r3 since m << M | |||
| where | |||
| G = 6.67259 * 10-11 N m2/kg2 | Universal gravitational constant | ||
| M = 5.98 * 1024 kg | Mass of the earth | ||
| m < 100,000 kg | Mass of the satellite | ||
| r | position vector of the satellite with respect to the centre of the earth | ||
| a | acceleration vector of the satellite towards the earth | ||
 |
So the satellite is always attracted to the centre of the earth. However, to prevent it from falling into the earth, it has a tangential (to the gravitational acceleration) velocity.
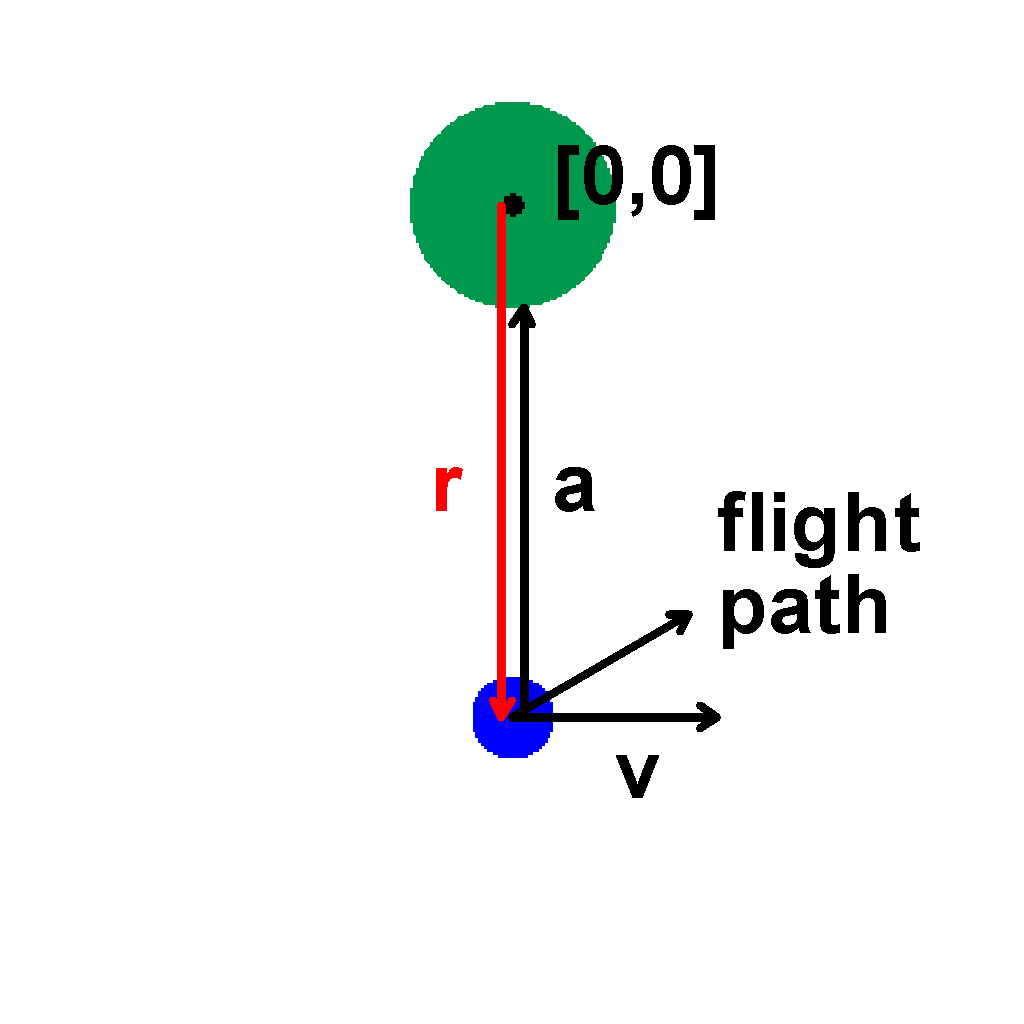 |
After combining the forces, we have some flight path vector between the two vectors, a and v |
We know that mechanical energy, E, is conserved.
| E | = kinetic energy + potential energy = a constant called "specific mechanical energy" | |
| = v2/2 - GM/r | ||
| = -GM/2a | ||
| where 2a is the length of the semi-major axis of the elliptical orbit | ||
It is from these observations that we see how to change from a lower orbit to a higher orbit.
| v2/2 - GM/r | = -GM/2a | |
|
v2/2 |
= GM* (1/r - 1/2a) |
Let's look at if we increase the velocity (at perigee) but keep the perigee distance constant. This gives a new E'.

|
This is going to cause the satellite to go further out because it has more velocity. Mathematically, r must increase to account for the increased v to maintain E' constant. |
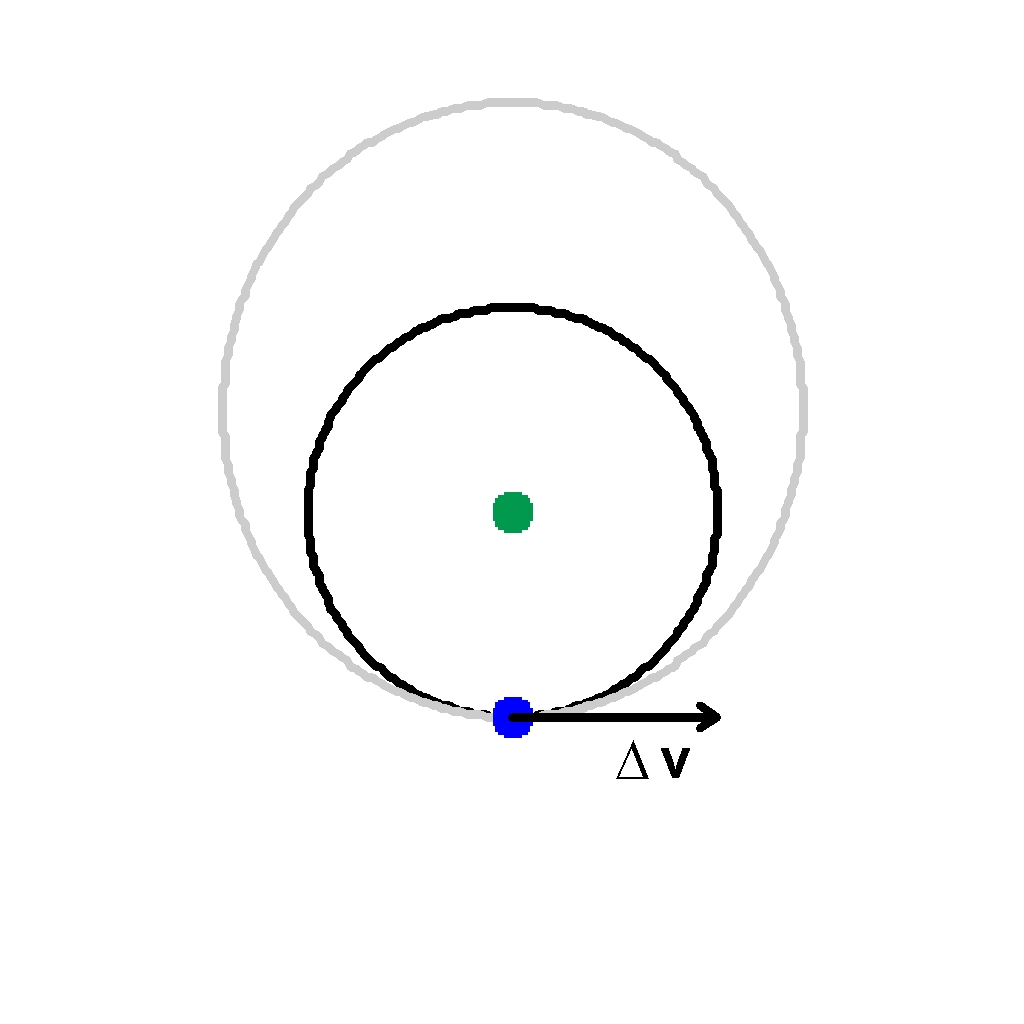
|
Now we have a larger orbit, but it is elliptical and not circular as we wished. Therefore, we apply the same principal again when the satellite is at apogee. |
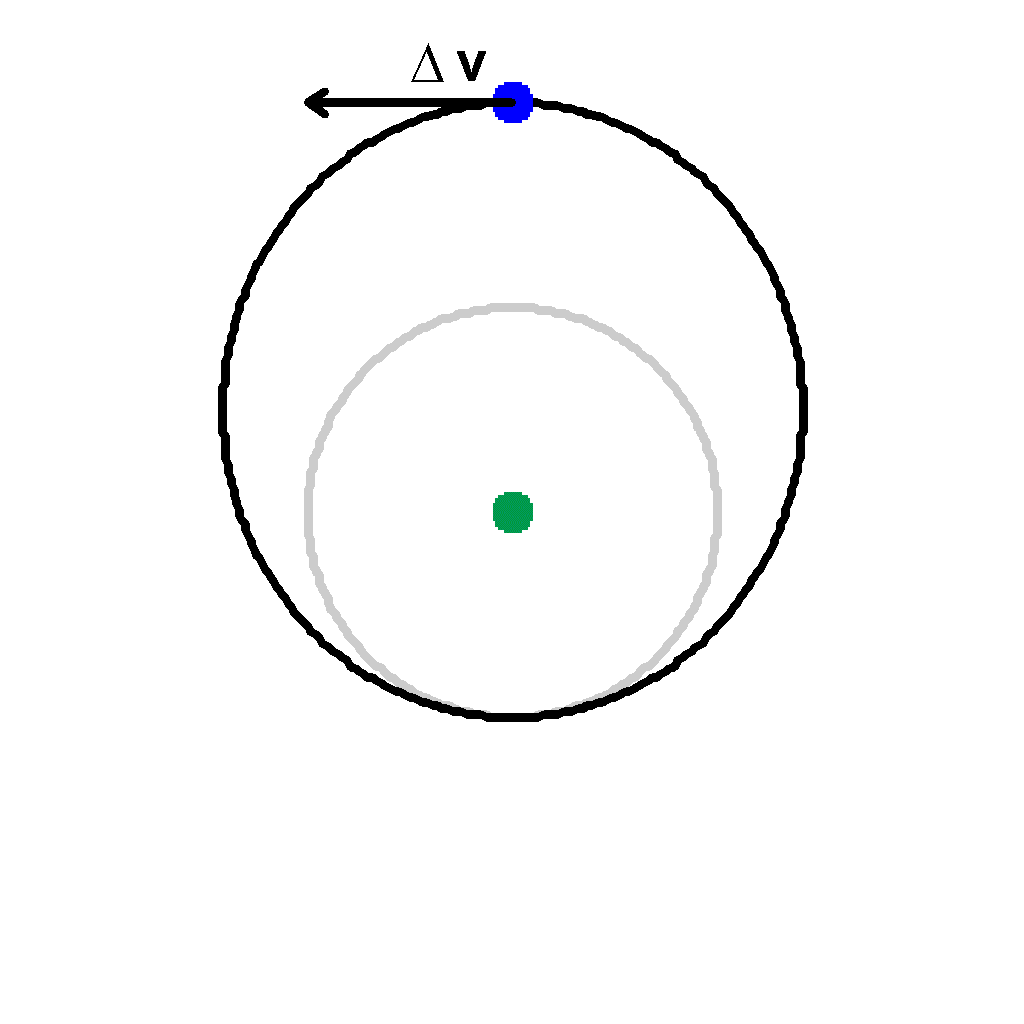
|
Apply another increase in velocity at apogee to enlarge the orbit again so the orbit becomes circular. |
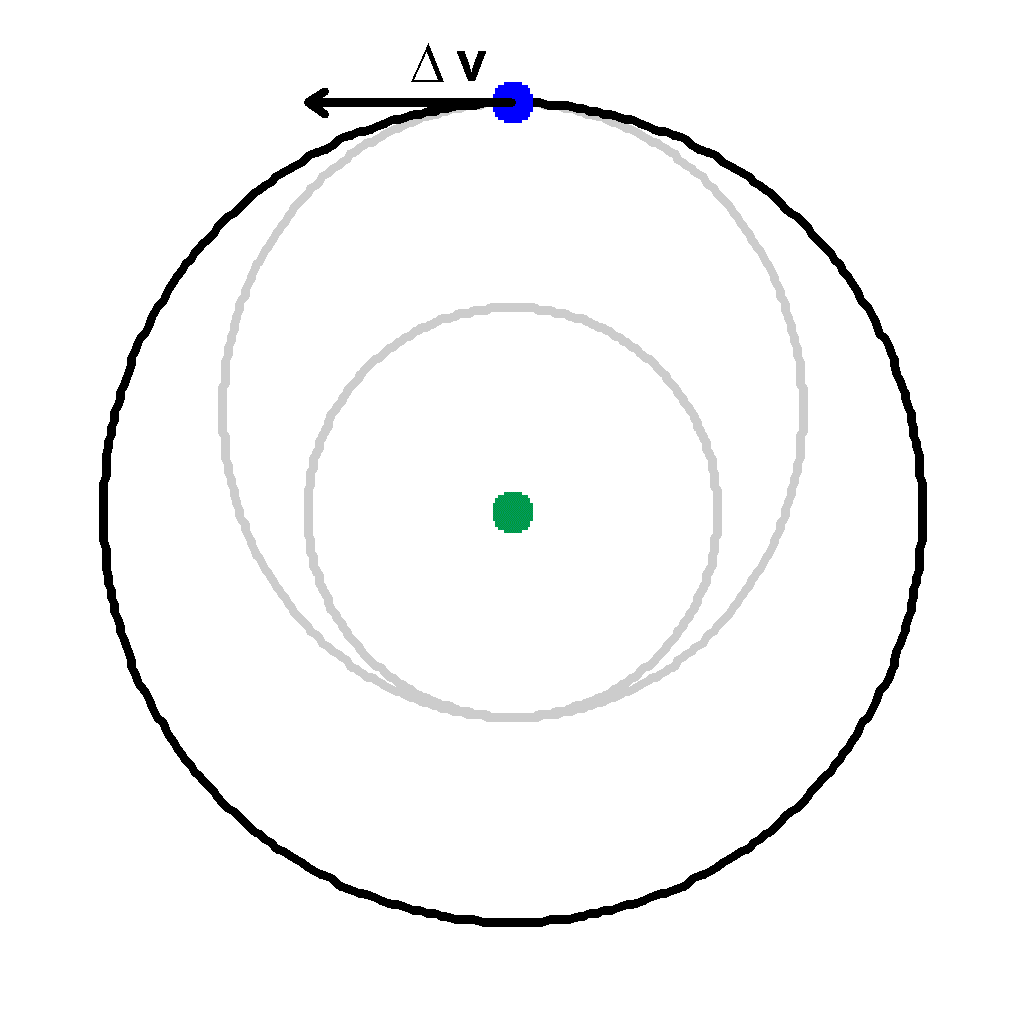
|
Now the satellite will move in the higher circular orbit. |
We can see that the time taken to move from the low orbit to the high orbit is one-half the elliptical orbit's period. This orbital change is called a Hohmann Transfer and requires the least amount of energy for an orbital change. However, it also takes the longest amount of time.
We can find the length of time taken. The period of an orbit is related to a3/2
| P | = 2*pi*a3/2 / (GM)1/2 |
Let's look at what happens when we increase v by a small amount.
| E | = v2/2 - GM/r = -GM/2a |
To find what an increase in velocity will do, solve for v.
| v2 | = GM ( 2/r - 1/a) |
We want to change the velocity but keep r constant, so we differentiate both sides.
| 2vdv | = GM (1/a2)da |
Now we want to find the increase in a, ie what da is, for a given dv increase.
| da | = a2 *2v*dv / (GM) |
Hence, the whole axis, 2a, increases by 2*da.
Now if we make a velocity increase at perigee, then r stays constant but a increases.
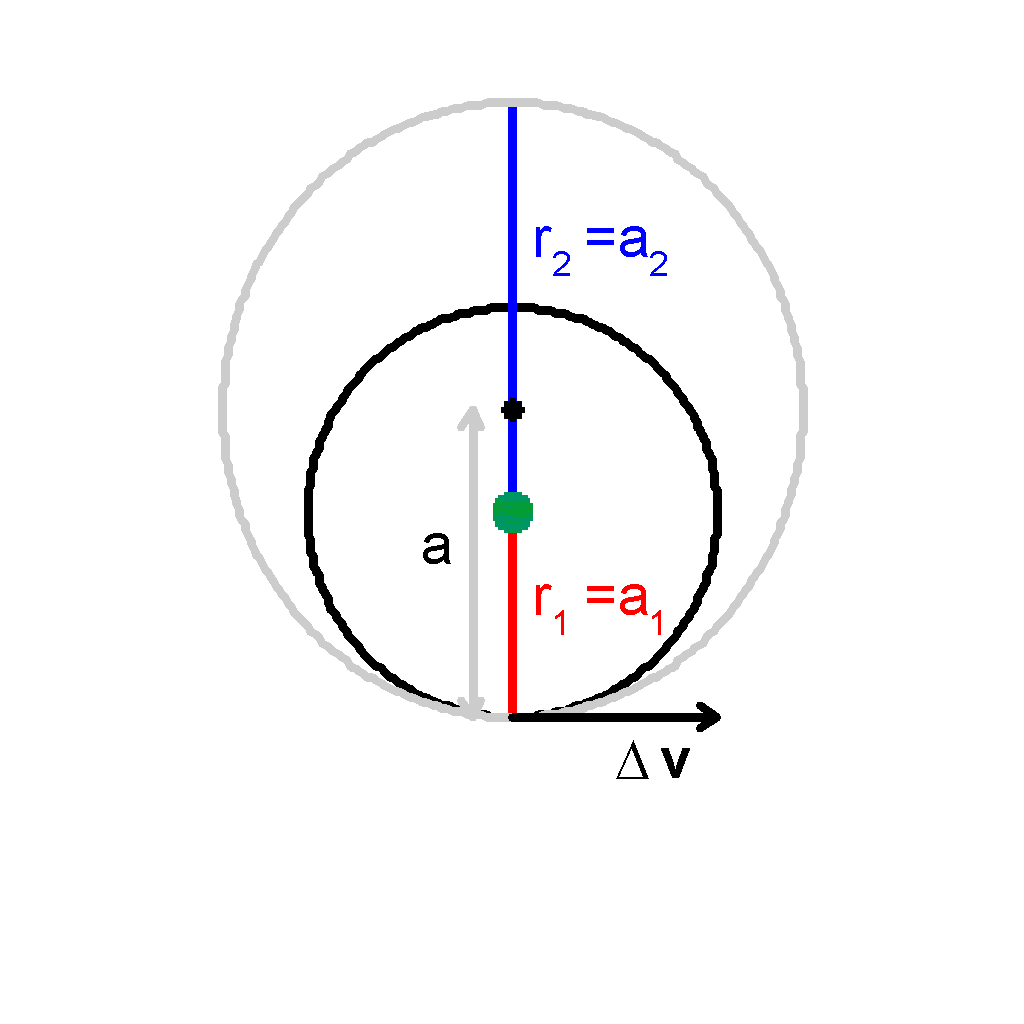
|
As we can see, the apogee increases in distance. |
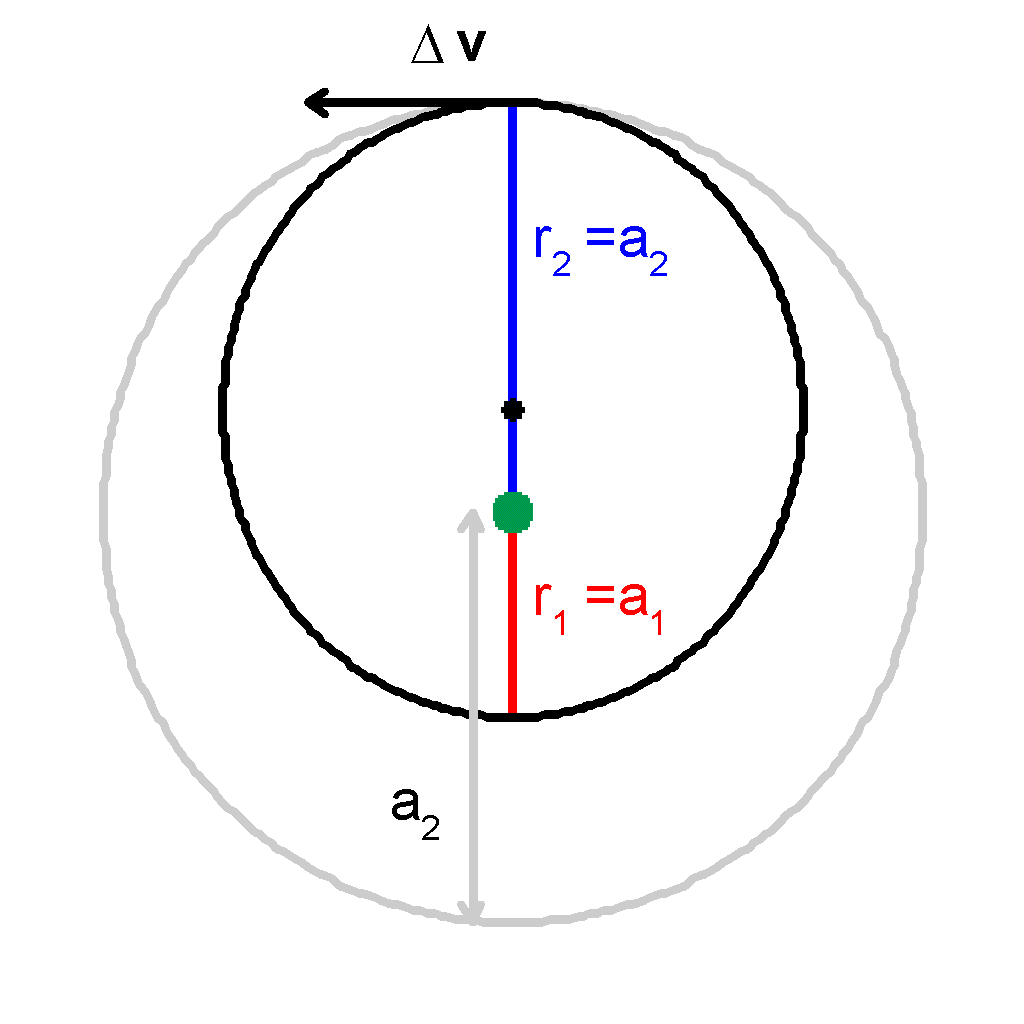
|
Likewise, if we apply the velocity increase at apogee, r2 will stay the same and a will increase, thus increasing the perigee distance. |

|
At perigee, we want to increase a such that the new a of the ellipse will make the ellipse be tangent to the higher circular orbit. |
| Thus to make a circular orbit change we can calculate the velocity increases needed at perigee and apogee and then change from the lower circular orbit to the elliptical orbit and from the elliptical orbit to the higher circular orbit by applying these velocity increases. | |
| We have | ||
| da | = 2a2v*dv / (GM) | |
| And we know for the ellipse that | ||
| 2ae | = r1 + r2 | |
| r2 | = ah | |
| So we want da to equal the difference of the radii of the two circles | ||
| da | = ah - al = r2 - r1 | |
| At perigee of the lower circular orbit, we have | ||
| vl 2 | = GM (2/r1 - 1/al ) = GM (2/r1 - 1/r1 ) = GM/r1 | |
| vl | = (GM/r1)1/2 | |
| Then we want the velocity of the ellipse at perigee to be | ||
| vep 2 | = GM (2/r - 1/a ) = GM (2/r1 - 2/(r1 + r2 )) | |
| = GM (2r2 / [r1(r1 + r2 )]) | ||
| vep | = (GM (2r2 / [r1(r1 + r2 )]))1/2 | |
| Thus we need the velocity change to be | ||
| vep-vl | = (GM (2r2 / [r1(r1 + r2 )]))1/2 - (GM/r1)1/2 | |
| = (GM)1/2 [(2r2 / [r1(r1 + r2 )])1/2 - 1/r1 1/2] | ||
|
Similarly, for changing from the ellipse to the higher circular orbit. |
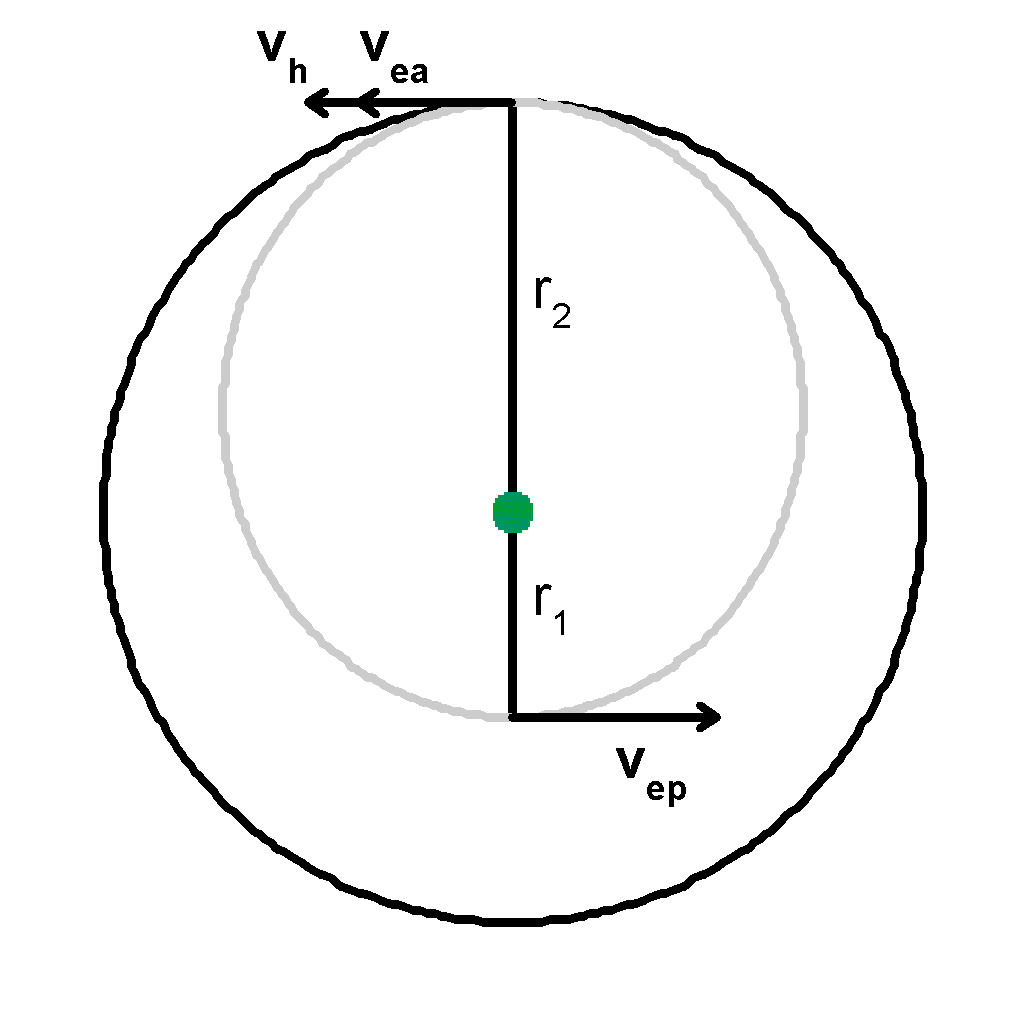
| We find the velocity of the higher circular orbit (at apogee or anywhere) | ||
| vh 2 | = GM (2/r2 - 1/ah ) = GM (2/r2 - 1/r2 ) = GM/r2 | |
| And the velocity at apogee of the ellipse is | ||
| vea 2 | = GM (2/r - 1/a ) = GM (2/r2 - 2/(r1 + r2 )) | |
| = GM (2r1 / [r2(r1 + r2 )]) | ||
| And we find the velocity incresase as | ||
| vh-vea | = (GM (2r1 / [r2(r1 + r2 )]))1/2 - (GM/r1)1/2 | |
| = (GM)1/2 [1/r2 1/2 - (2r1 / [r2(r1 + r2 )])1/2 ] | ||
| We now know the velocity increases we need for each orbital change. | ||
| And the time required is 1/2 the period of the elliptical orbit | ||
| Pell | = 2 * pi * a3/2 / (GM)1/2 | |
| Ttranfer | = pi * a3/2 / (GM)1/2 = [pi / (GM)1/2 ] * [(r1 + r2 )/2]3/2 | |
Example
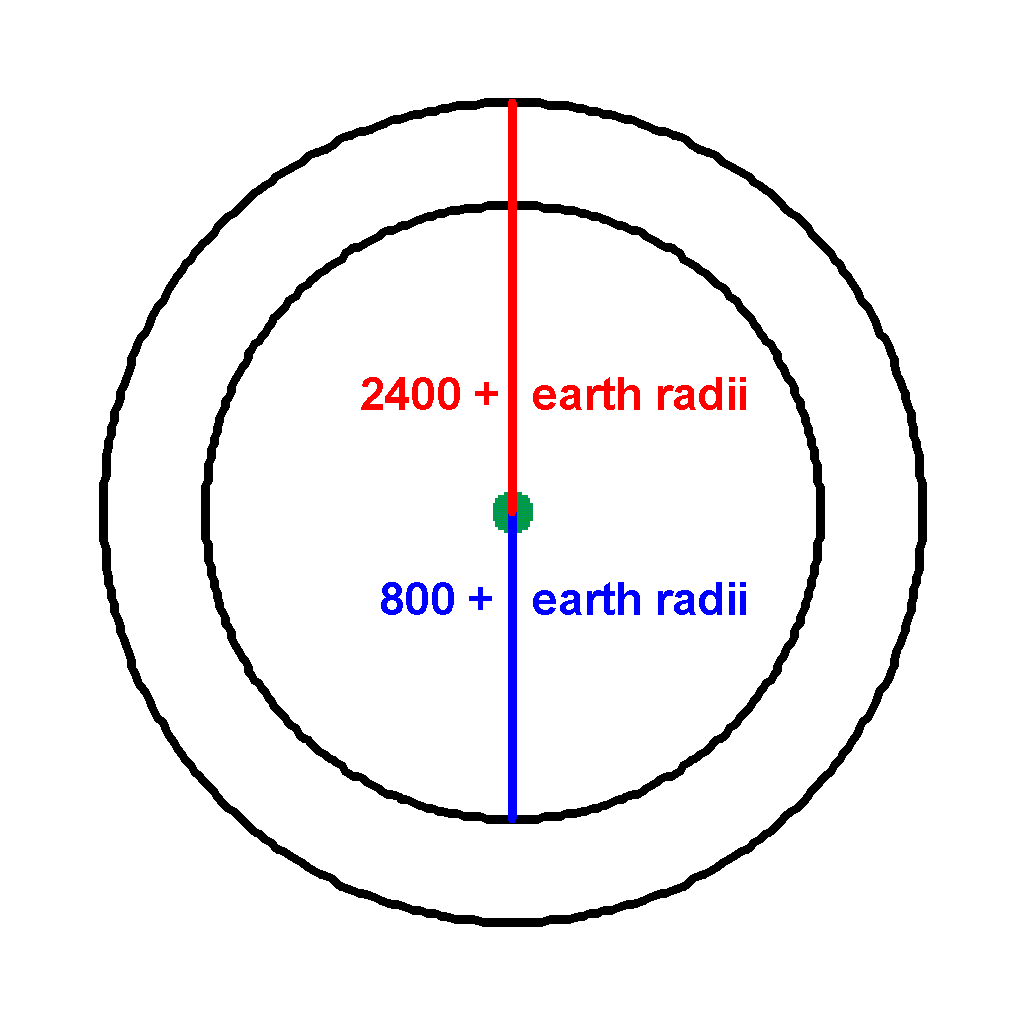
Let's consider changing from a low earth orbit of 800km above the surface to another low earth orbit of 2400km.
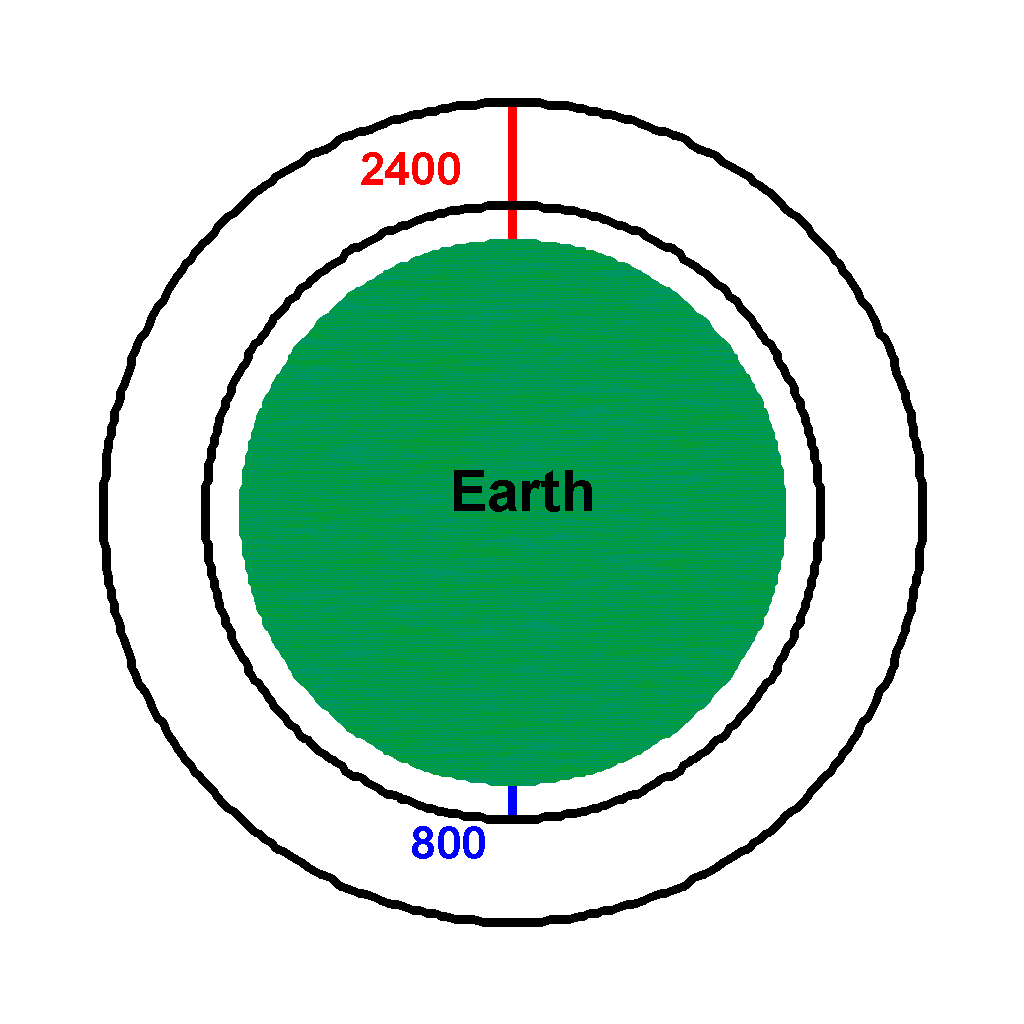 |
 |
| Let's define our constants | |||
| GM | = 3.986032 * 105 km3 / s2 | ||
| Radius of Earth | = RE = 6378.165 km | ||
| Let | r1 | = 800 km + 6378.165 km | |
| = 7178 km | |||
| r2 | = 2400 km + 6378.165 km | ||
| = 8778 km | |||
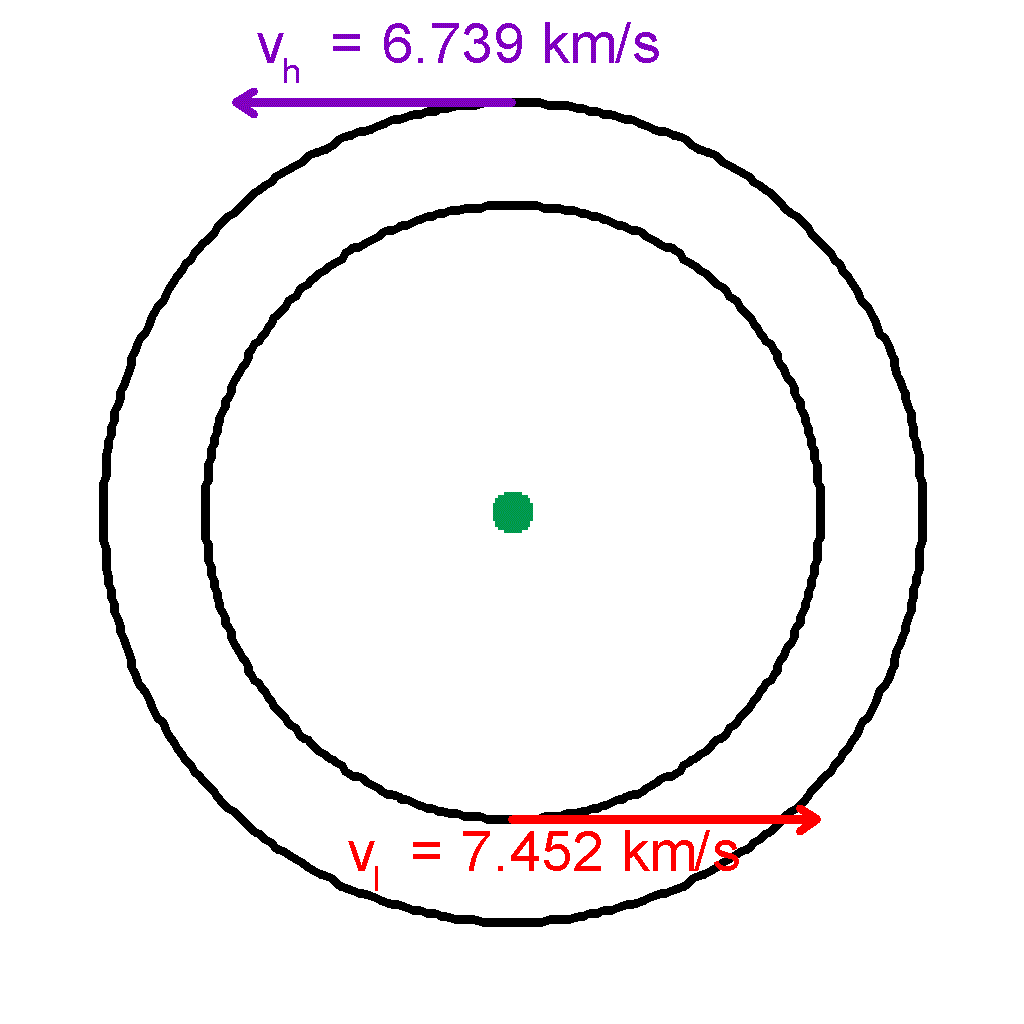
| We find the velocity of the lower orbit | |||
| vl | = (GM / r1 )1/2 | ||
| = [(3.986 * 105 km3 / s2) (1/7178km)]1/2 | |||
| = 7.452 km/s | |||
| Similarly for the higher orbit | |||
| vh | = (GM / r2 )1/2 | ||
| = [(3.986 * 105 km3 / s2) (1/8778km)]1/2 | |||
| = 6.739 km/s | |||
|
|
|
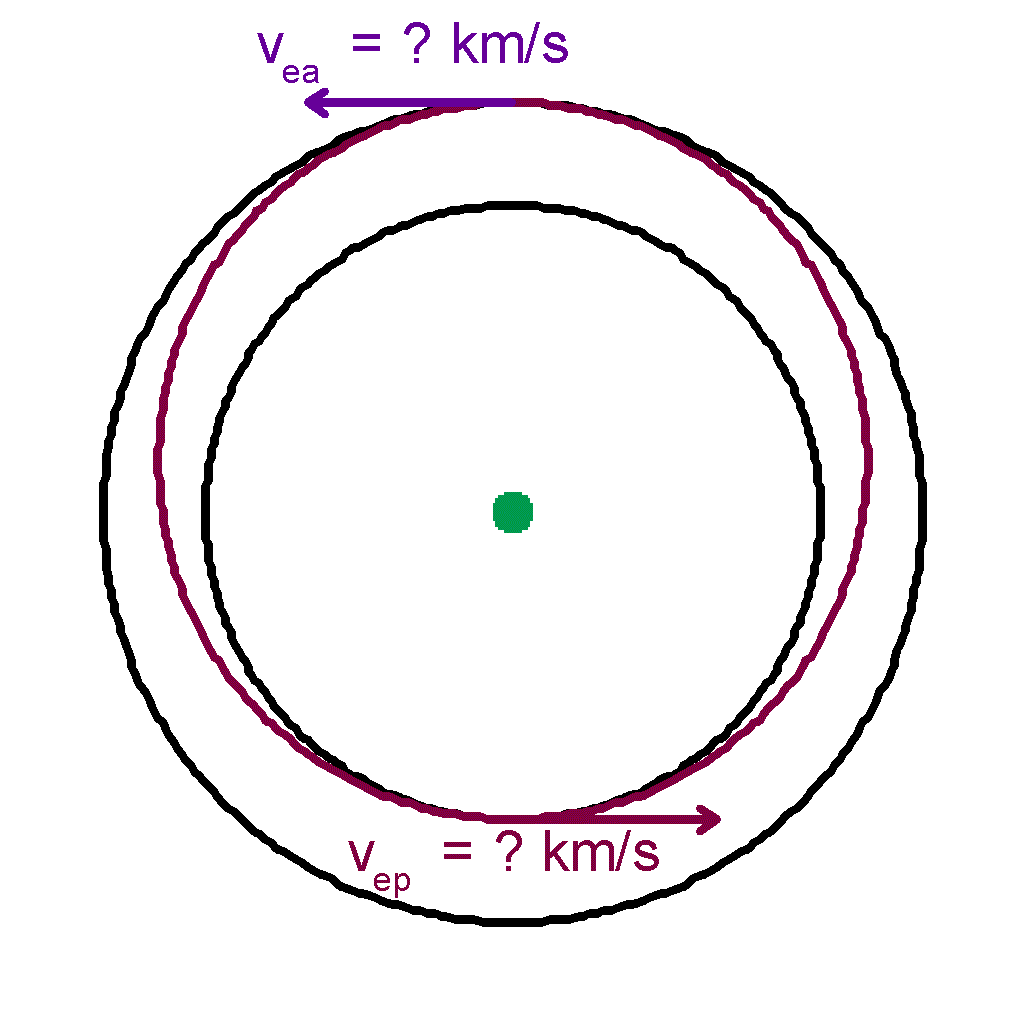
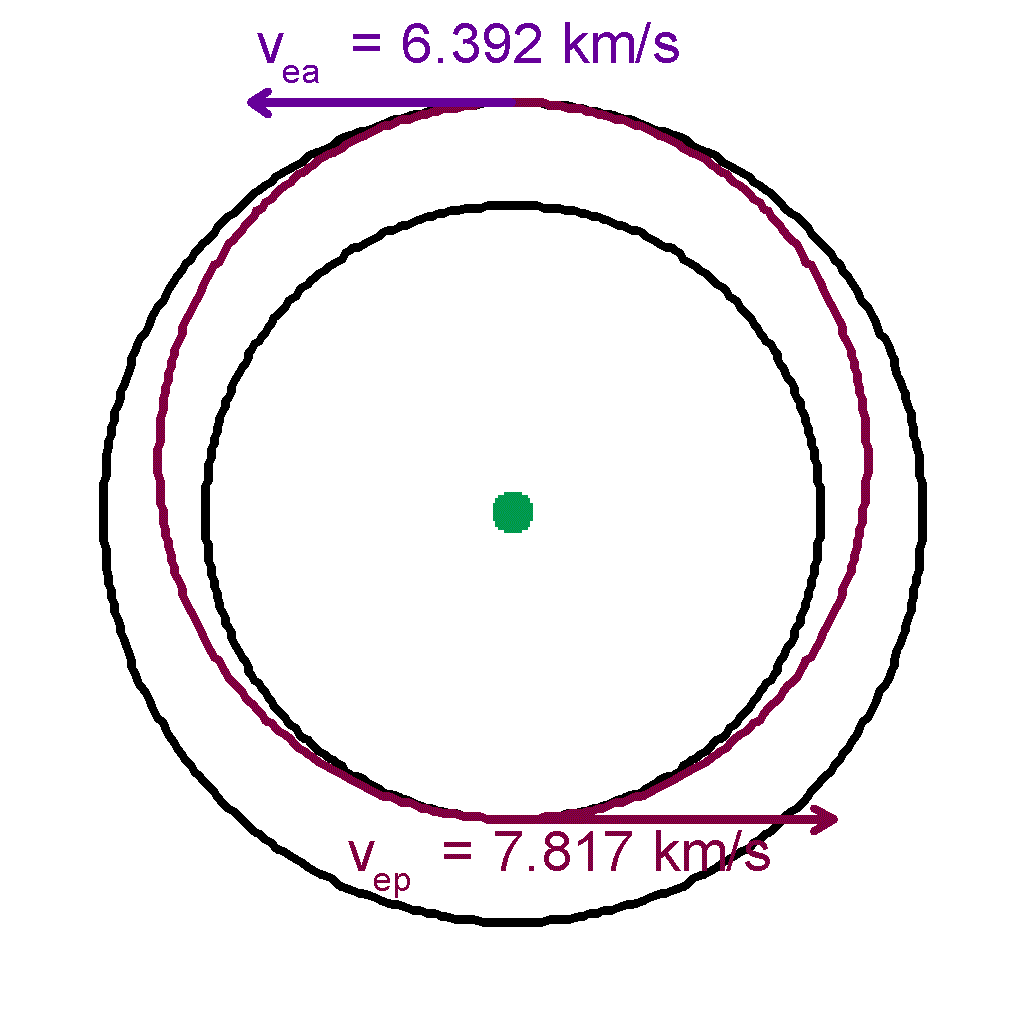
Now we want to find the velocity of the ellipse that passes through these two points at perigee and apogee. |
| The velocity at perigee is | |||
| vep 2 | = GM (2r2 / [r1(r1 + r2 )]) | ||
| = [(3.986 * 105 km3 / s2) (2*8778km / (7178km * (7178km+8778km)))]1/2 | |||
| = 7.817 km/s | |||
| And at apogee of the ellipse | |||
| vea 2 | = GM (2r1 / [r2(r1 + r2 )]) | ||
| = 6.392 km/s | |||

|
|
| Velocities for circular orbits | Velocities of elliptical orbit |
| Thus, we find that we first need an increase of velocity of | |||
| vep - vl | = 7.817 km/s - 7.452 km/s | ||
| = 0.365 km/s | |||
| And at apogee, we need to increase by | |||
| vh - vea | = 7.452 km/s - 6.392 km/s | ||
| = 1.06 km/s | |||
| to move the satellite into the higher circular orbit | |||
| Now that we have the elliptical orbit defined, we can calculate the length of time this orbit change takes | |||
| a | = r1 + r2 / 2 |
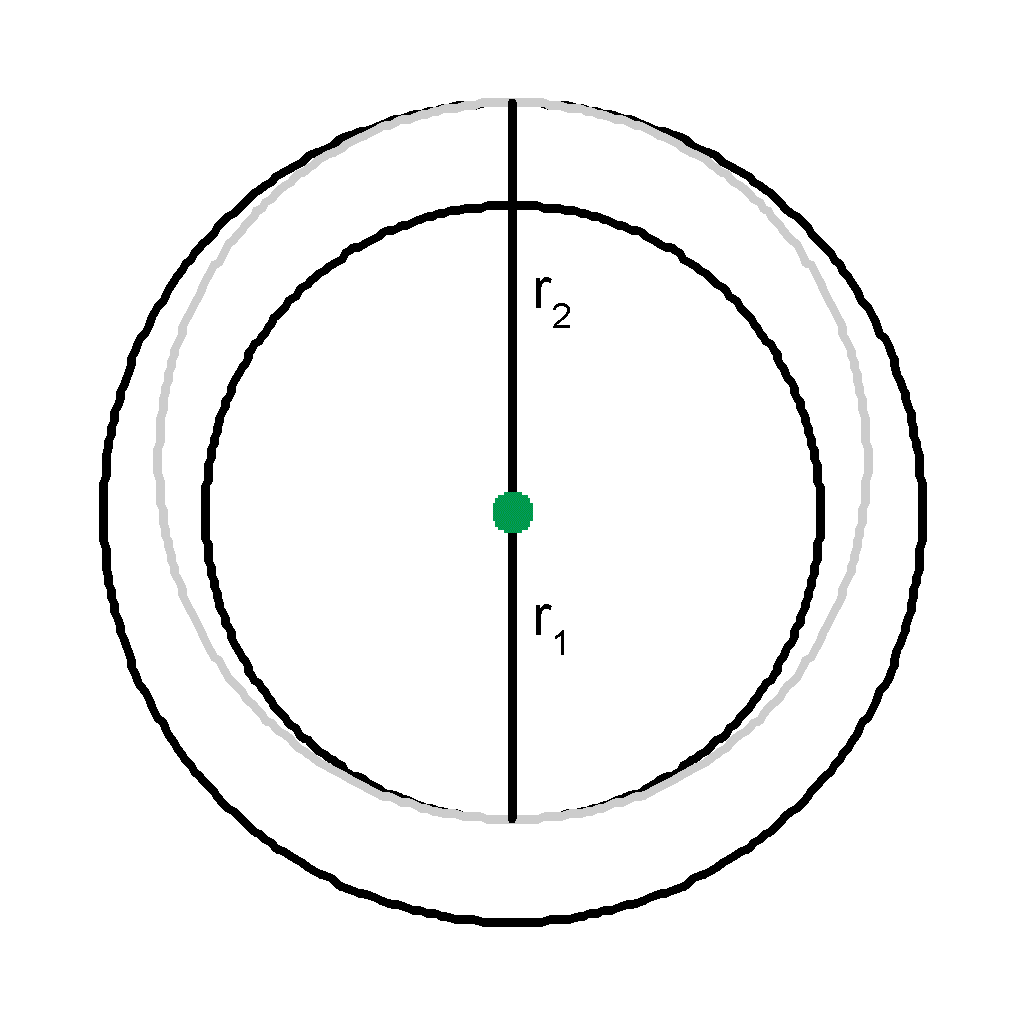
|
|
| Ttranfer | = [pi / (GM)1/2 ] * [(r1 + r2 )/2]3/2 | ||
| = [pi / (GM)1/2 ] * [(7178km + 8778km)/2]1/2 | |||
| = 3546 sec = 59 min 6 sec | |||
| We can view the movement of the satellite as it goes along the elliptical orbit in its transfer. Note that its velocity is not constant since the satellite is fastest at perigee and slowest at apogee. Thus, after one-half of its transfer time, it has traveled more than one-half of the required transfer distance. | |||
| Here the satellite's movement is broken into six steps of 3546/6 = 591 seconds each. | |||
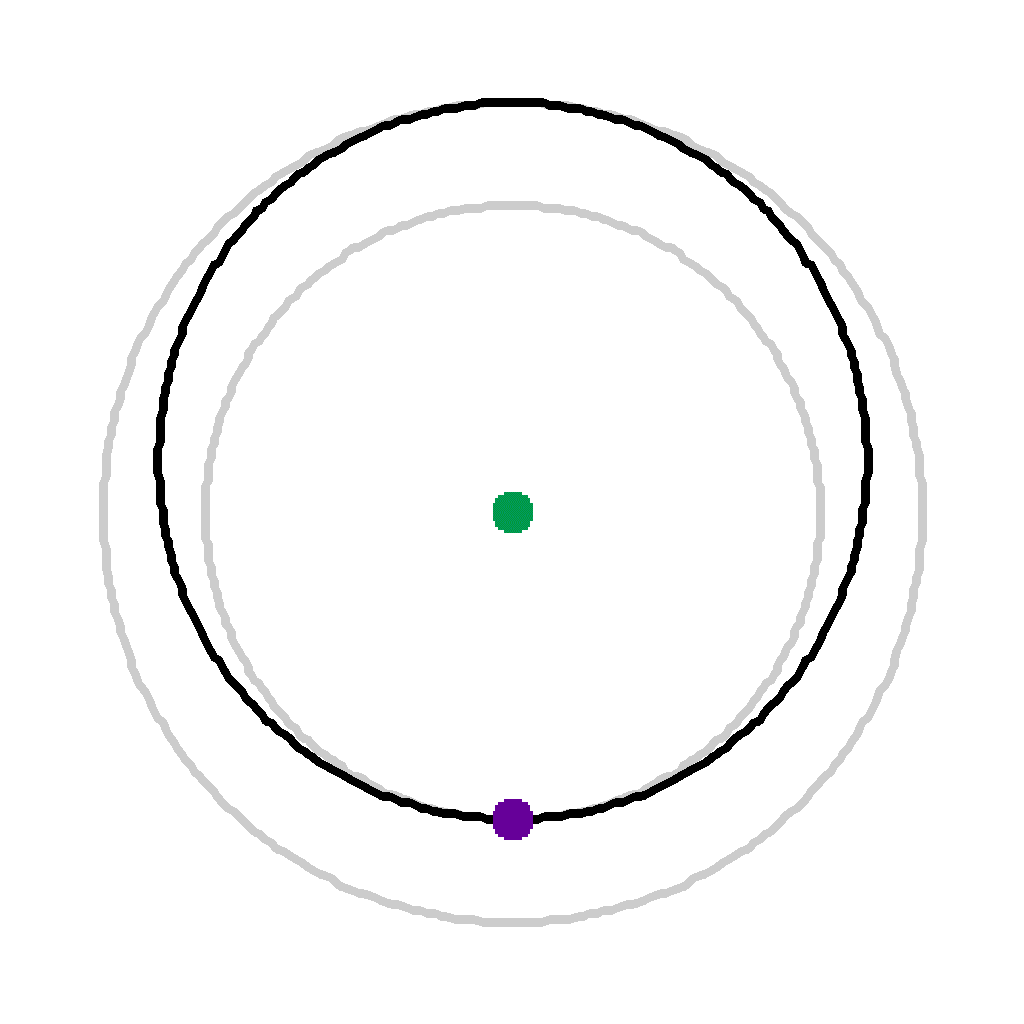
|
Time 0 (0 secs) | Satellite is instantaneously accelerated |
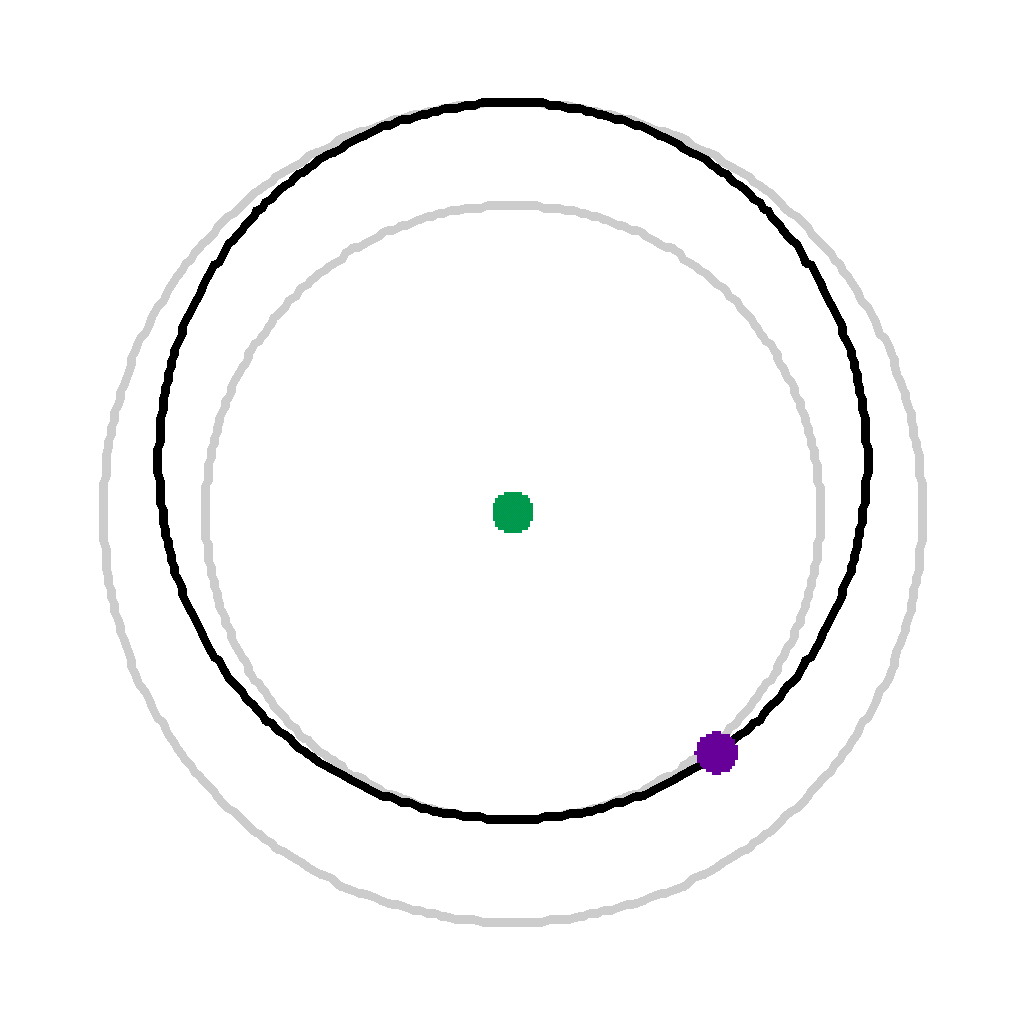
|
Time 1 (591 secs) | |
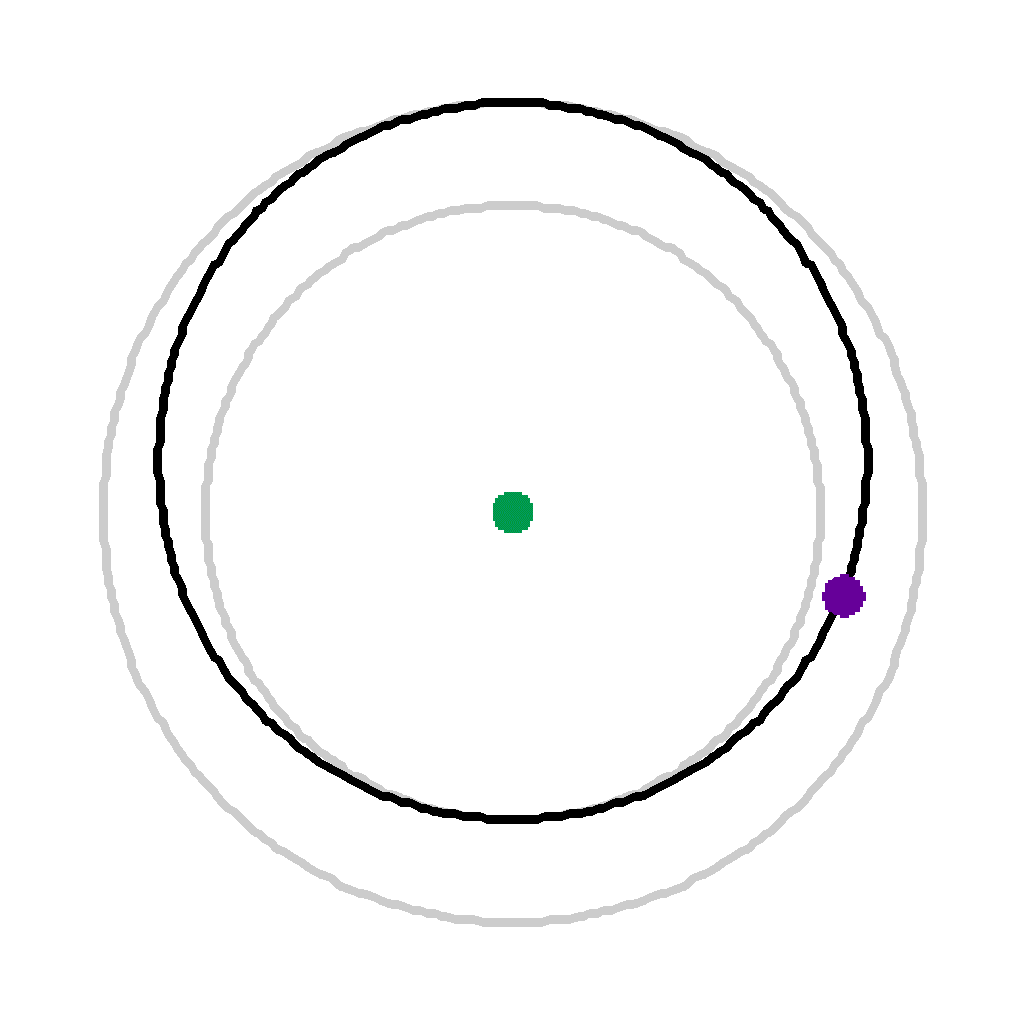
|
Time 2 (1182 secs) | |
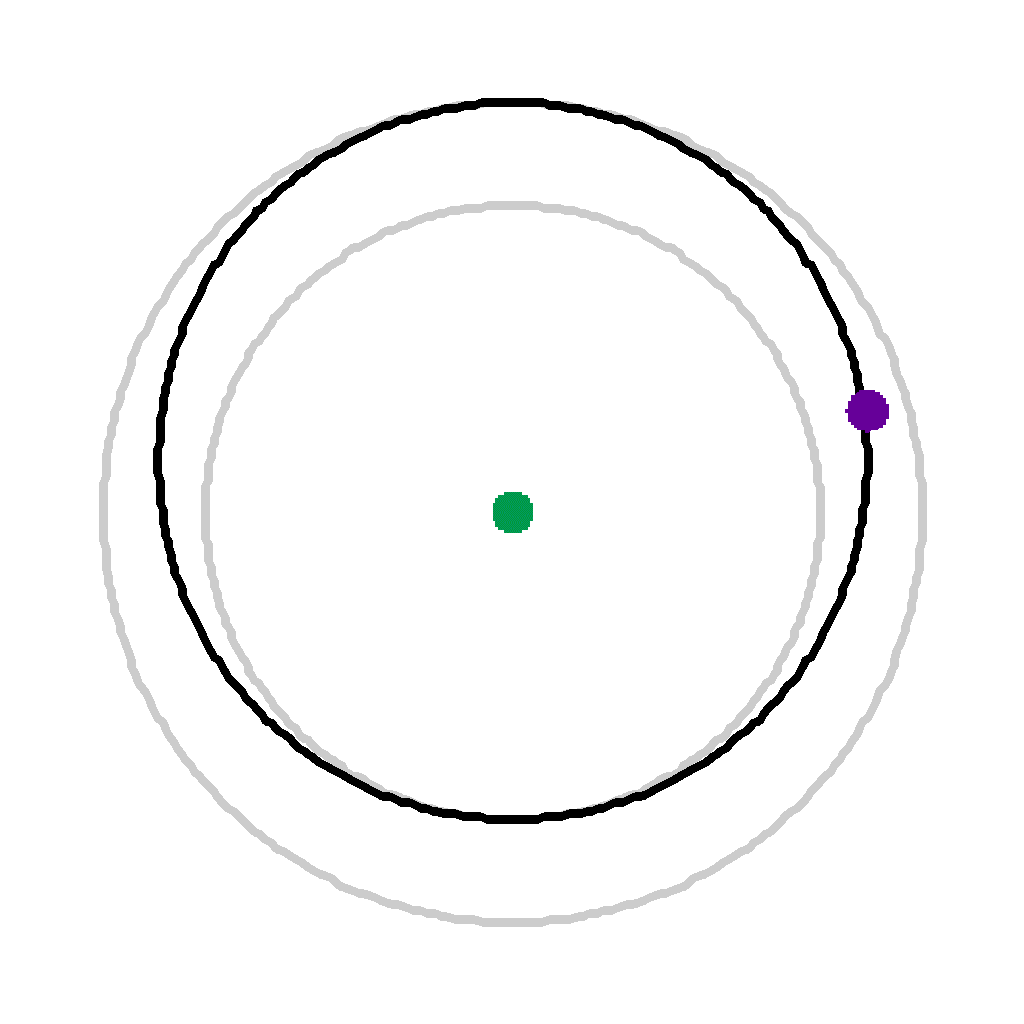
|
Time 3 (1773 secs) | After 1/2 its transfer time, it has traveled more than 1/2 of its transfer distance. |

|
Time 4 (2364 secs) | |
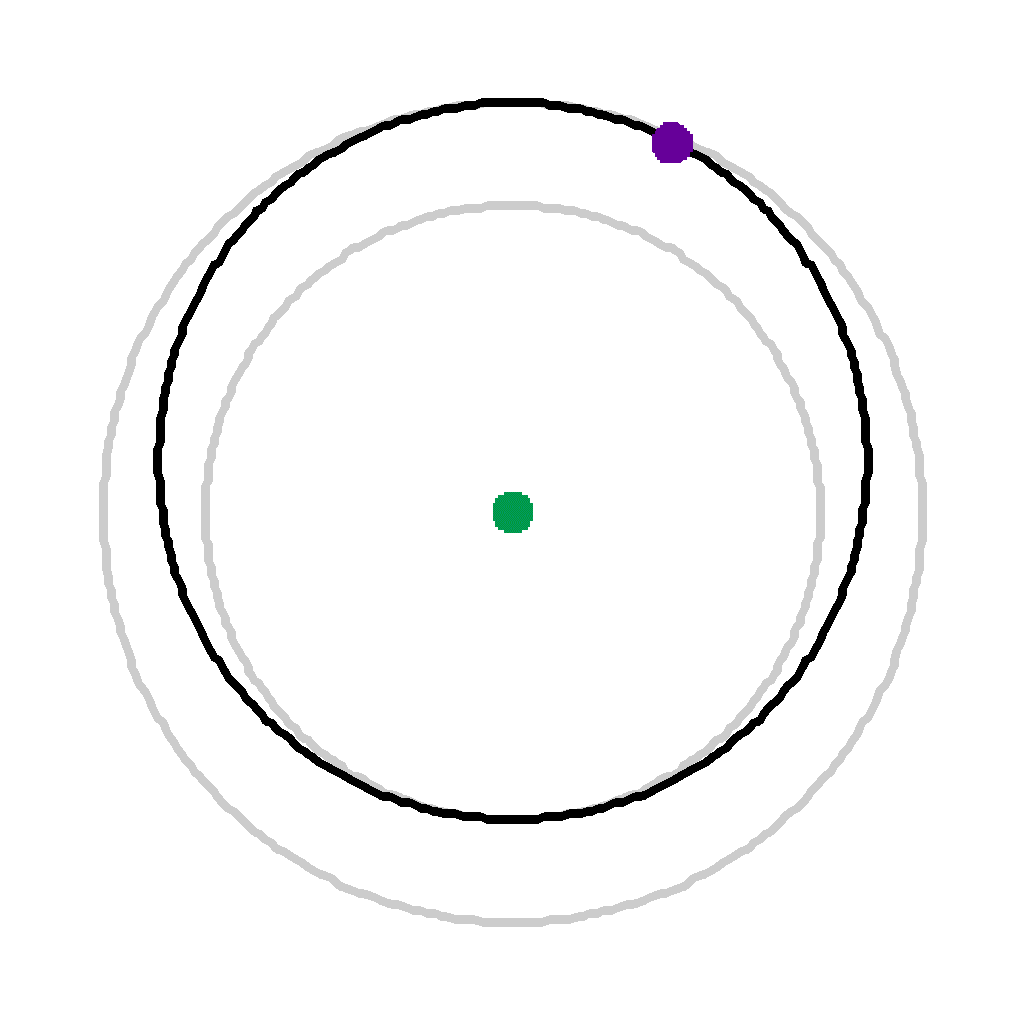
|
Time 5 (2955 secs) | |
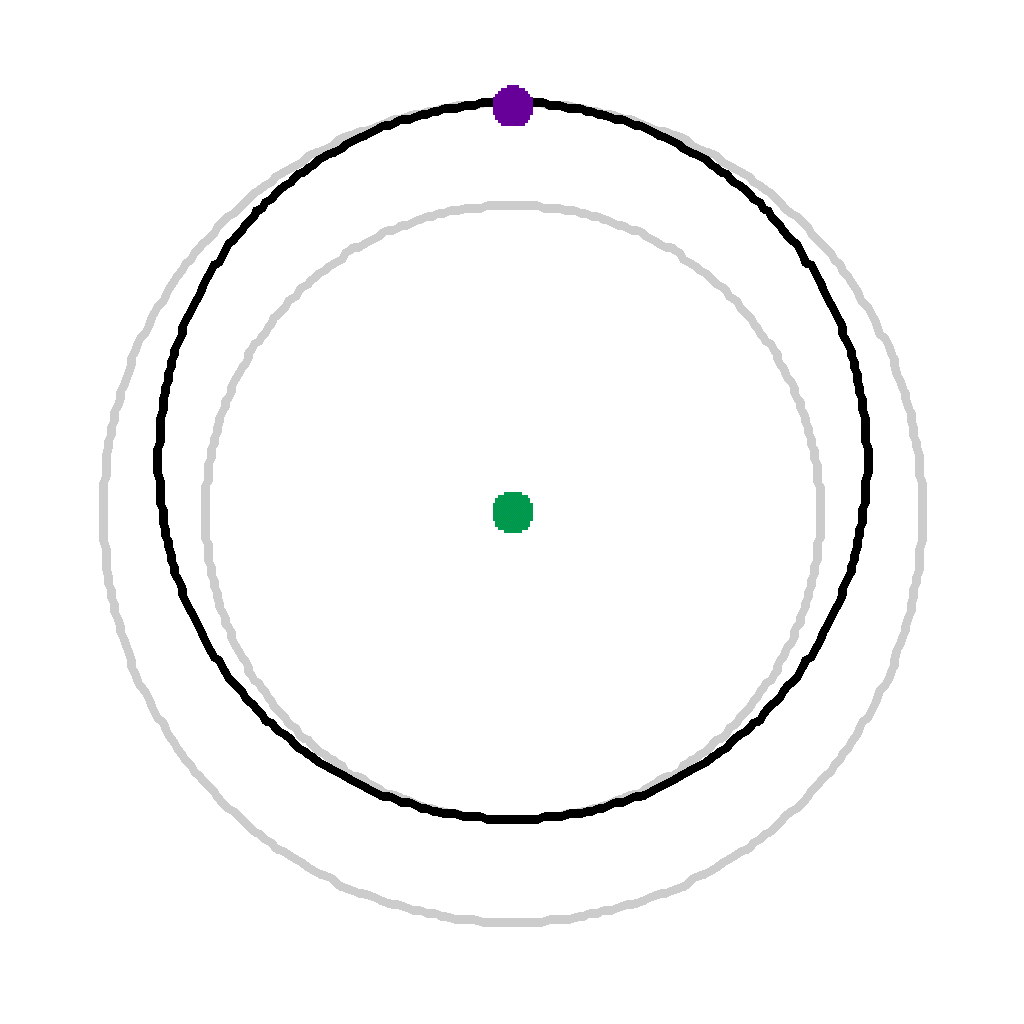
|
Time 6 (3546 secs) | Satellite is again instantaneously accelerated to change from the elliptical orbit to the higher circular orbit. |
|
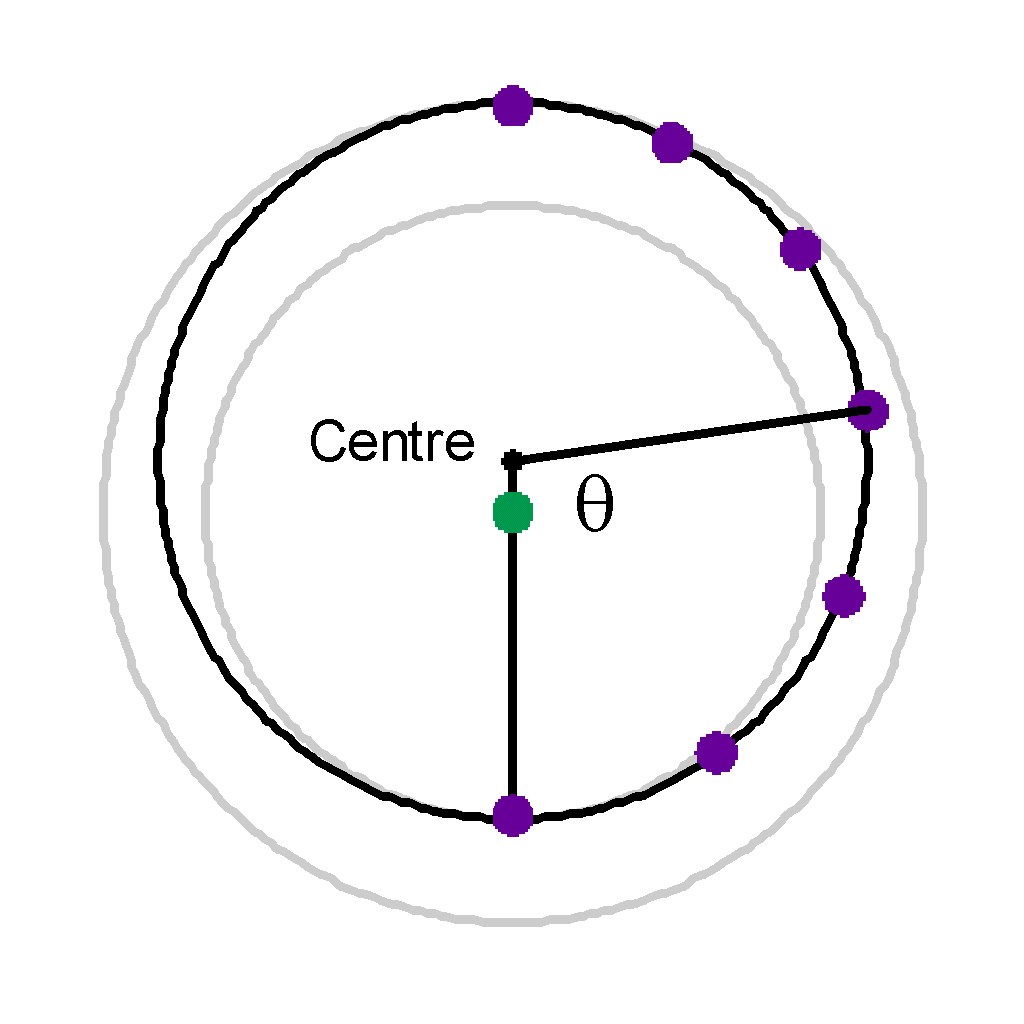
Here we can see that after the 3 steps, the angle theta made with the centre
of the ellipse > pi/2. Hence it has gone more than 1/4 of the total
elliptical distance.
Also, we can visually see that the distance between the first satellite plots are further apart than those plotted near the top at apogee. |
|
So we have seen what shapes earth orbits are and why. We have also seen how to transfer from a lower orbit to a higher orbit. The reverse, a transfer from a higher orbit to a lower orbit is done the same way but velocity decreases are used instead of increases.
Another area to look at for satellite orbits is to take the earth's oblateness into account. Because the earth bulges around the equator, this actually rotates the orbit around the earth. Depending on the orbit of the satellite, this can cause as much as 9 degrees a day in change.
April 27, 2001
My main reference for the understanding this material and the derivation of the equations was Fundamentals of Astrodynamics by Roger Bate.