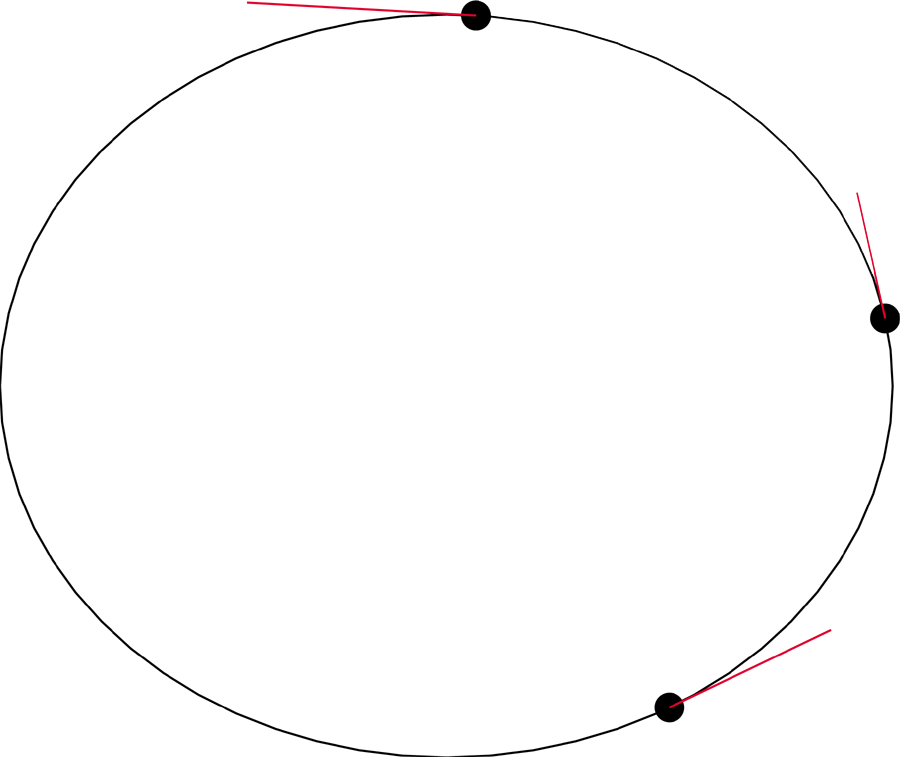
From Newton's Principia, given three points and the velocities at those points, we can determine the focus around which the planet orbits.  That is, the centre to which the planet is attracted.
 

This can be done by extending the tangents to where they meet, and extend inwards a line perpendicular to the tangents, length inversely proportional to the velocity.
 
 

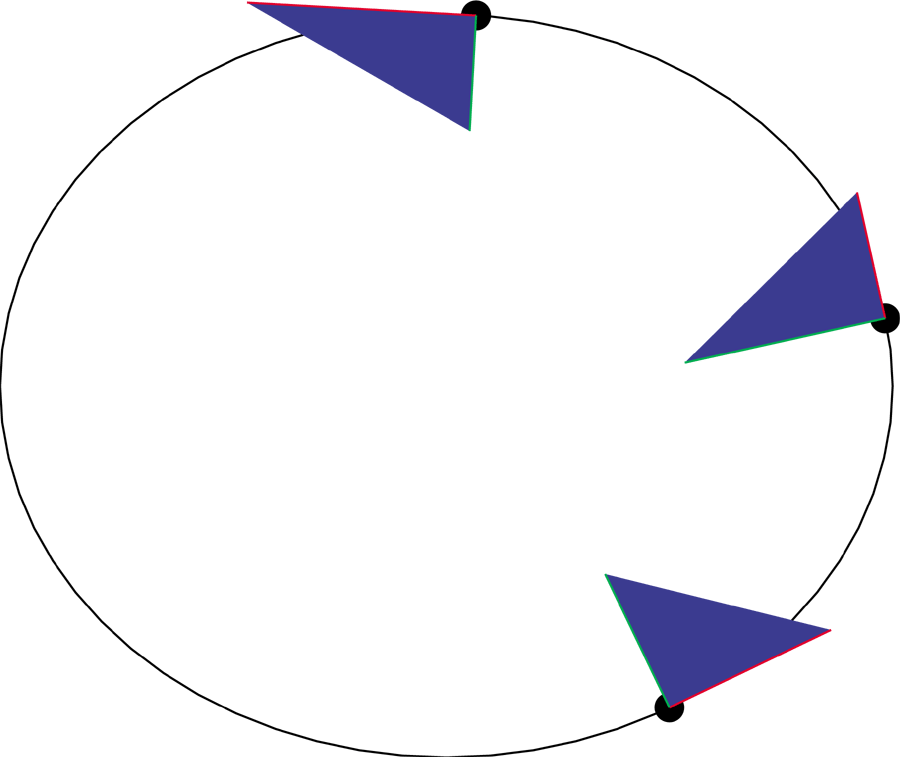
The inverse of the velocity can be found by producing a right triangle with equal area with one side the velocity vector.  The other side will be inversely proportional to it.
 

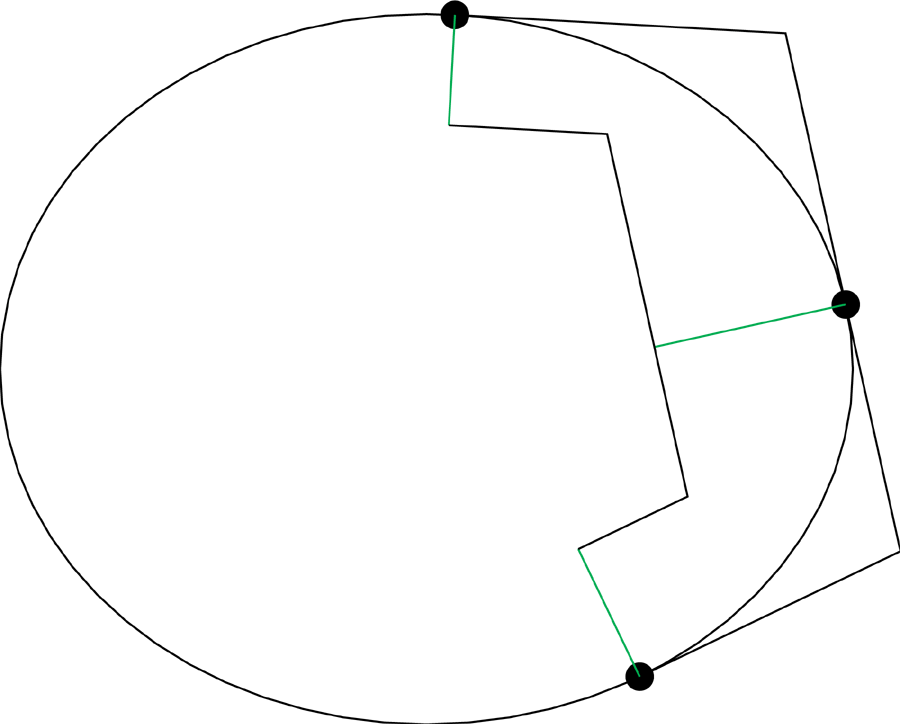
Now we cap the inward normals with lines parrallel to the tangents, and intersect these.
 

The line passing through the intersection of the tangents and the intersection of the "caps" will also path through the focus.  Therefore with three points, we can find two lines through the focus, so their intersection is the focus.

Why is this?
 

We first must understand angular momentum, which is what governs the speed of an orbiting planet.  It is the product of the velocity , the weight (a constant in our case), the radius and the sine of the angle between them.  It is more easily seen an area between the velocity vector and the radius vector.
 

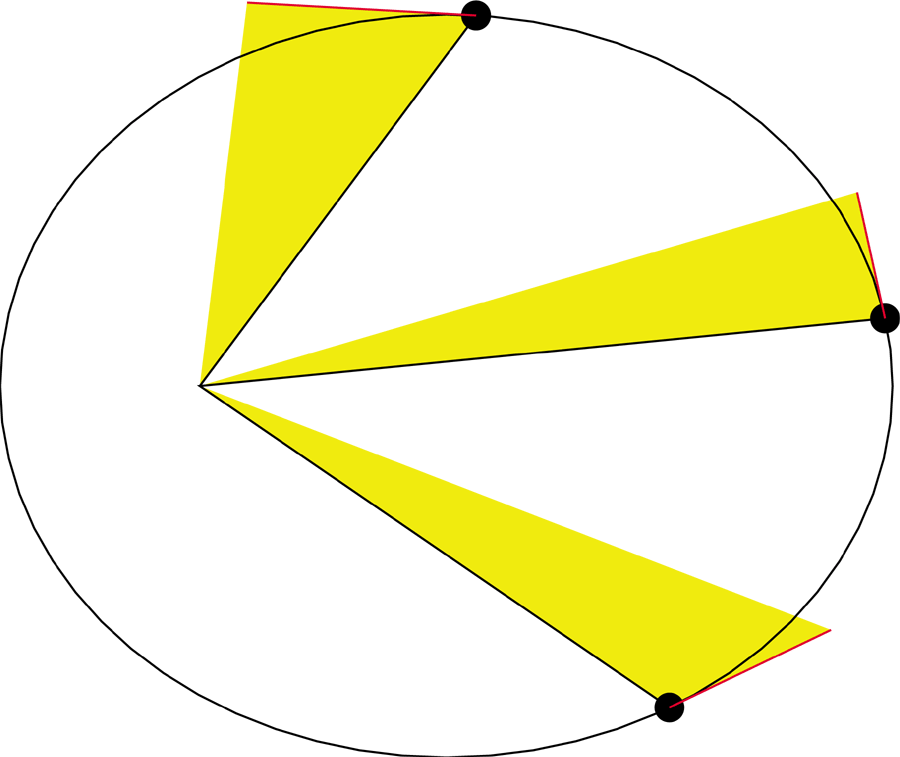
For an orbiting planet, the angular momentum is constant, so the areas of the yellow triangles are all equal.

Also, if we shear the triangles along the tangents until one of their edges are perpendicular, their areas stay equal, and the we now see that the normal to the tangent is inversely proportional to the velocity. 
 

Now, both the lines perpendicular to the tangent are inversely proportional to the velocity, they are directly proportional to each other.
 

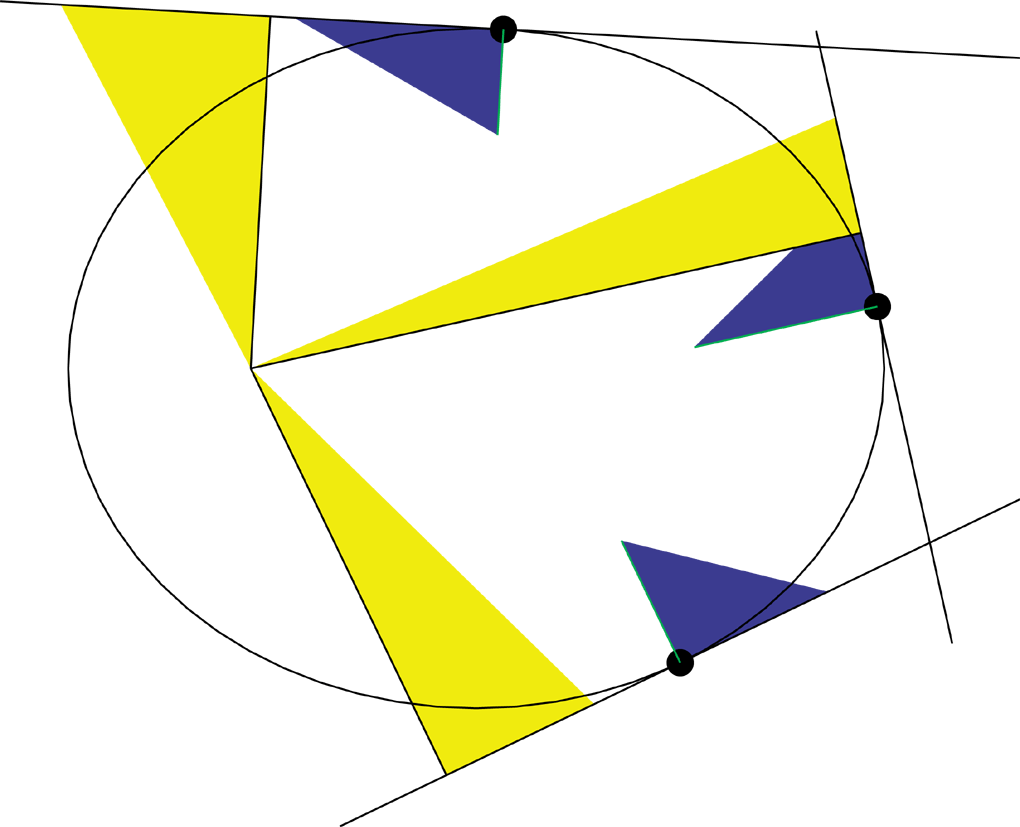
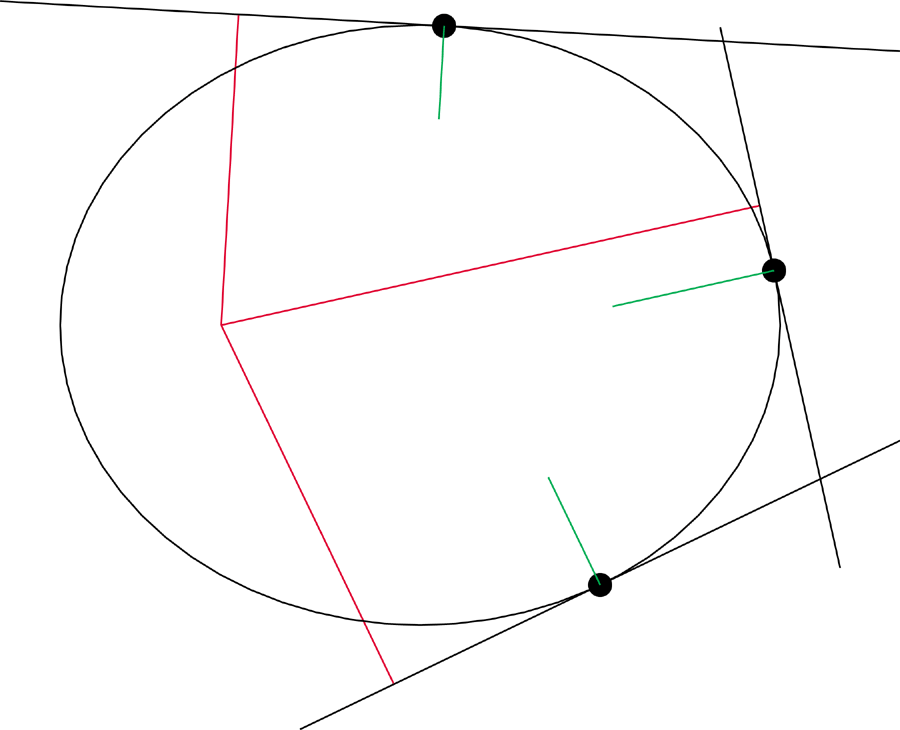
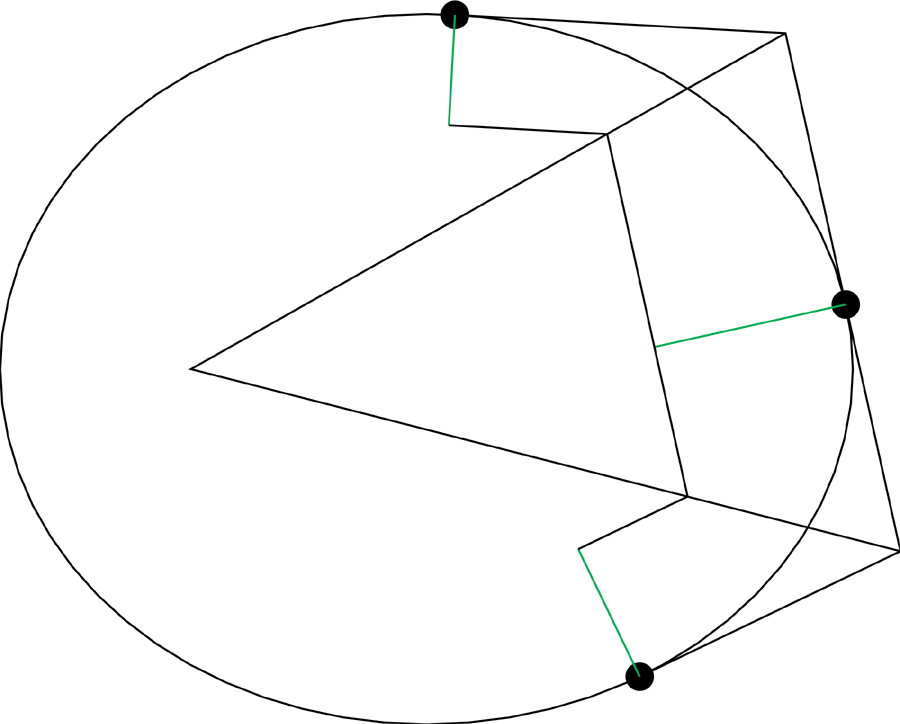
Reconstructing Newton's diagram, we can now add what we know about the relation between the inverse of the velocity and the distance form the tangent to the focus.  If we translate the inverse of the velocity over to the intersection of the "caps", we see something very interesting.......
 

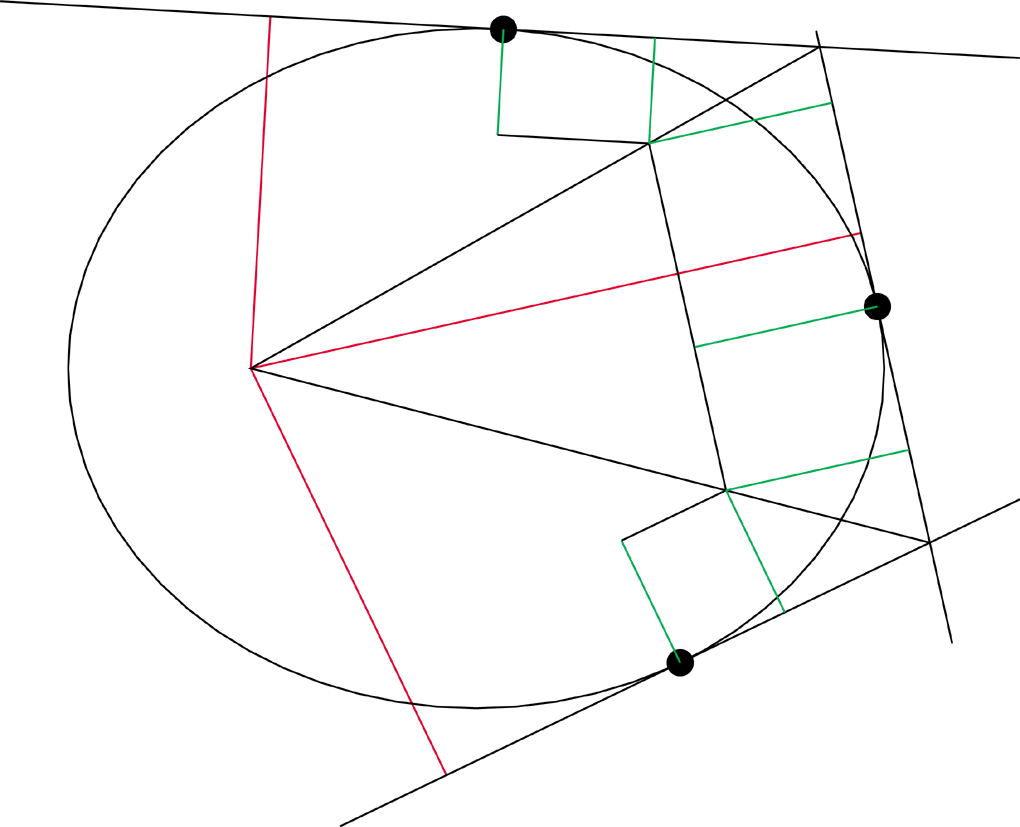
The quadrilaterals created by the inverses are similar to the quadrilaterals created by the normals to the tangents, so the line that cuts the first in half, also cuts the larger in a similar fashion, so that this line does path through the focus.
 

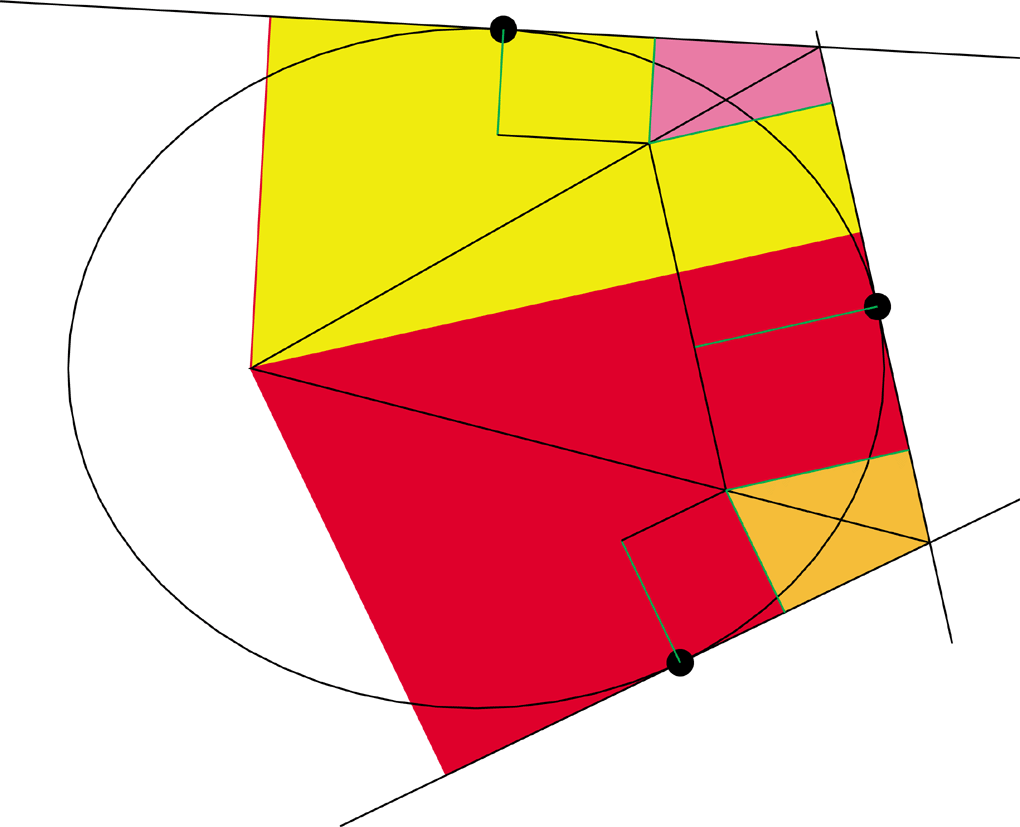
QED