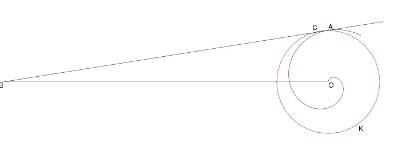
Archimedes' Spiral

Background

Click Below to Download Individual Ghostscript Files (.ps format)

• Archimedes' Tangent

• Proposition 7

• Proposition 8

• Proposition 14

• Proposition 15 and Corollary

Propositions 18 and 19

I.      If OA be the initial line, A the end of the first turn of the spiral, and if the tangent to the spiral at A be drawn, the straight line OB drawn from ) perpendicular to OA will meet the said tangent in some point B, and OB will be equal to the circumference of the "first circle".

Click on pictures to download Ghostscript files.

Proof:

Suppose OB is greater than c, the circumference of the first circle.

Suppose OB is less than c, the circumference of the first circle.

Since OB is not less than or greater than c, OB = c.

II.     If A' be the end of the second turn, the perpendicular OB will meet the tangent at A' in some point B', and OB' will be equal to 2(circumference of the "second circle").

Proof:

Suppose OB is greater than 2c', twice the circumference of the second circle.

Suppose OB is less than 2c', twice the circumference of the second circle.

Since OB is not less than or greater than 2c', OB = 2c'.

III.     Generally, if A_n be the end of the nth turn, and OB meet the tangent at A_n in B_n, then
 OB_n = nc_n,
where c_n is the circumference of the "nth circle"

The proof for this is similar to the proofs for the first and second circles.

Reference

Heath, T.L.  Archimedes. Dover Publications Inc. New York.  Reprint of 1897 Heath Addition.

A Math 309 Project By Darien Shannon
April 19, 2001