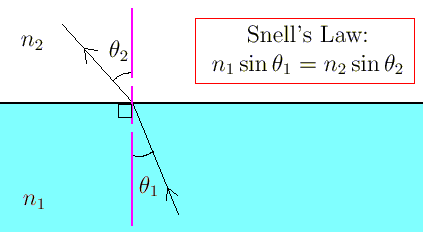
When light travels from one medium to another, it generally bends, or refracts. The law of refraction gives us a way of predicting the amount of bend. This law is more complicated than that for reflection, but an understanding of refraction will be necessary for our future discussion of lenses and their applications. The law of refraction is also known as Snell's Law, named for Willobrord Snell, who discovered the law in 1621.
Like with reflection, refraction also involves the angles that the incident ray and the refracted ray make with the normal to the surface at the point of refraction. Unlike reflection, refraction also depends on the media through which the light rays are travelling. This dependence is made explicit in Snell's Law via refractive indices, numbers which are constant for given media1.
Snell's Law is given in the following diagram.
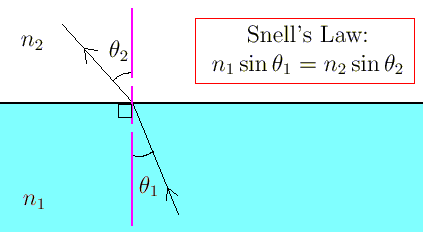
As in reflection, we measure the angles from the normal to the surface, at the point of contact. The constants n are the indices of refraction for the corresponding media.
Tables of refractive indices for many substances have been compiled.
| n for Light of Wavelength 600 nm | |
|---|---|
| Substance | Refractive Index, n |
| Air (1 atmosphere pressure, 0 degrees C) | 1.00029 |
| Water (20 degrees C) | 1.33 |
| Crown Glass | 1.52 |
| Flint Glass | 1.66 |
Say, in our simple example above, that we shine a light of wavelength 600 nm from water into air, so that it makes a 30o angle with the normal of the boundary. Suppose we wish to find the angle x that the outgoing ray makes with the boundary. Then, Snell's Law gives
Refraction certainly explains why fishing with a rod is a sport, while fishing with a spear is not2.
A more complicated illustration of Snell's Law proves something that seems intuitively correct, but is not obvious directly. If you stand behind a window made of uniform glass, then you know by now that the images of the things on the other side of the window have been refracted. Assuming that the air on both sides of your window have the same refractive indices, we have the following situation:
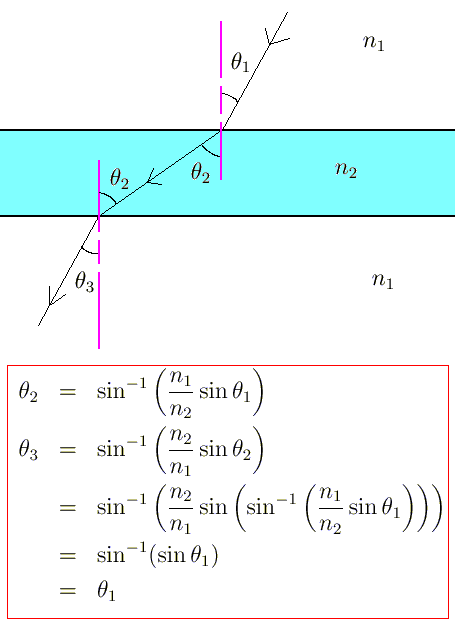
We find that the incoming and outgoing light beams are actually parallel.
Rearranging Snell's Law, with i and r being the incident and refracted angles,
a qualitative description of refraction becomes clear. When we are travelling from an area of higher index to an area of lower index, the ratio n1/n2 is greater than one, so that the angle r will be greater than the angle i; i.e. the refracted ray is bent away from the normal. When light travels from an area of lower index to an area of higher index, the ratio is less than one, and the refracted ray is smaller than the incident one; hence the incident ray is bent toward the normal as it hits the boundary.
Of course, refraction can also occur in a non-rectangular object (indeed, the objects that we are interested in, lenses, are not rectangular at all). The calculation of the normal direction is harder under these circumstances, but the behaviour is still predicted by Snell's Law.
Given a transparent substance, we can always find its index of refraction by using a setup like the example above. Surrounding the substance of unknown index n with a material with a known index of refraction, we can find the unknown n by measuring angles and applying Snell's Law.
However, calculating ns in this way, an obvious question arises. How did the first index get calculated? We could always choose an arbitrary substance as a meterstick, and calculate all other indices in terms of this base. However, indices of refraction arise in Maxwell's equations for electromagnetic waves; that, in fact, is how they are defined. We shall not delve into these equations here; instead we will note that n for air is very close to 1, and that we can therefore easily calcuate n for any other substance using our setup above.
An interesting case of refraction can occur when light travels from a medium of larger to smaller index. The light ray can actually bend so much that it never goes beyond the boundary between the two media. This case of refraction is called total internal reflection.
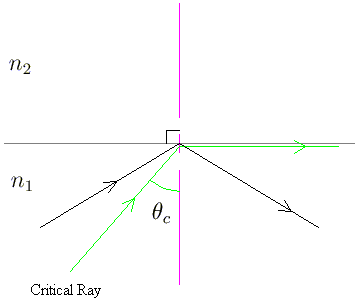
In the above diagram, imagine that we are trying to send a beam of light from a region with refractive index n1 to a region with index n2 and that n2 < n1. If x1, x2 are the angles made with the normal for the incident and refracted rays, then Snell's Law yields
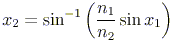
Since n2 < n1, we could potentially get an argument for the arcsin function that is greater than 1; an invalid value. The critical angle is the first angle for which the incident ray does not leave the first region, namely when the "refracted" angle is 90o. Any incident angle greater than the critical angle will consequently be reflected from the boundary instead of being refracted. For concreteness, pretend that we are shining light from water to air. To find the critical angle, we set x2 = 90o. Using Snell's Law, we see that any incident angle greater than about 41o will not leave the water.