
We call problems arising from a non-constant magnification of a lens distortion.
When the magnification of a lens differs at the edge of the lens and at the centre, the image of a square object will be abnormally curved.

In (a), the lens has too much magnification at its edges, causing a surfeit of magnification of the square at the corners. This is commonly called pincushion distortion (for the resulting shape), or positive distortion (for overmagnification). In (b), the lens has too little power at its edges, causing a barrel, or negative distortion.
Distortion can be explained using our basic position and magnification equations. We know that M = -i/s and 1/i + 1/s = 1/f. Solving in our position equation for i, we get

Substituting into our magnification equation, we find that
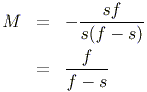
The magnification thus depends on the focus location. Now that we know that the distance from the optical axis has an effect on the focal length, we can infer from this that the magnification of a spherical lens is not constant.
Distortion is a paricularly vexing problem when one wishes to photograph large-scale structures such as buildings; the walls will seem to curve. Distortion is sometimes removed by using symmetric lens systems.