Effects with Cassini Ellipses
Standard Ellipse
By: Arsham Skrenes
There are a number of ways of describing an ellipse mathematically:
Cartesian equation: 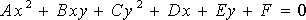
Parametric form: 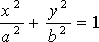
Gauss-mapped form: 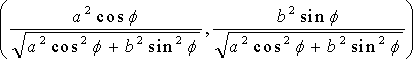
This is probably due to the fact that ellipses have a number of interesting properties. One such example is the fact that they can have two foci. I use this feature to demonstrate an interesting way of constructing an ellipse. To begin, you simply hammer in two nails into a single board. You then attach the ends of a single length of string to each nail. Finally, pushing outwards against the string with a pen you will draw a perfect ellipse with the foci at the nails. To illustrate this, click on the following graphic:
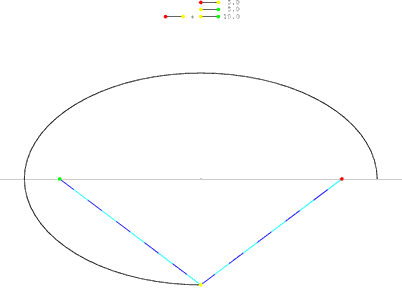
In this demonstration you will notice that the string stayed at a fixed length (you can visually see this by looking at the colors of the string or reading the numerical length above the diagram). This is because a standard ellipse has the following property:
All points on the ellipse represent the SUM of the distances from the two fixed points (the foci).