Effects with Cassini Ellipses
Cassini Ellipse
By: Arsham Skrenes
Named after Giovanni Cassini, the astronomer who also discovered the moons of Saturn, the Cassini ellipse is a modification on the pins-and-string construction of a regular ellipse. Unlike the regular ellipse, however, there is no known physical way to perform a pins-and-string construction of Cassini ellipses because it is constructed from the product of the distances instead of the sum. In other words, the Cassini ellipse has the following property:
All points on the ellipse represent the PRODUCT of the distances from the two fixed points (the foci).
This is fortunate for us because it gives us an insightful way of understanding the Cassini ellipses and their remarkable characteristics. Looking at the mathematical interpretations is not nearly as intuitive:
Cartesian equation: 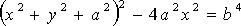
Bipolar equation: 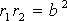
Polar equation: 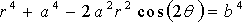
As mentioned before, there is no known way to physically perform the pins-and-string construction of Cassini ellipses; however, thanks to the ability of computer imaging, we can investigate this interesting and intuitive definition of Cassini ellipses.
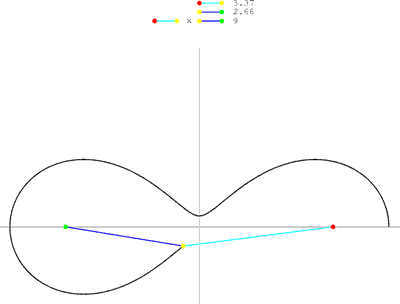
Notice how the product of the distances remains fixed. Since postscript is not interactive, I have included a lot of different scenarios of drawing Cassini ellipses – especially since these remarkable ellipses have such a variety of appearances based on the input variables. For an interactive Java version of this demonstration, be sure to follow up on my references.