The Mathematics of Artillery:
A Study in Modern Ballistics
Introduction
While for most
artillery users, the art of artillery has come down to inputting variables into
a computer program that is essentially a large experimentally derived spread
sheet, the science of ballistics has driven mathematics and physics for most of
the last millennium and complex theories have evolved around them. The trouble with ballistics is the
complexity of the formulas and the need for constant reevaluation in
flight.
Topics
History
The
study of ballistics began with the advent of the cannon which occurred
somewhere around 1327 when Edward III began producing Spingards, an early
cannon. For the next two centuries,
the mathematics of ballistics was left to those operating the cannons. At this point, it was believed that a
projectile would essentially travel in the same vector that they were fired and
would not deviate from this path more than from the inherent inaccuracies of
the device. Indeed, early in the
history of ballistic projectile warfare, cannons were more for show and fear
then for strategic value. As the
weapons became more reliable, gunners began to experiment with angles and power
compositions in an attempt to better aim their weapons.
Niccolo
Franco Tartaglia, an Italian mathematician, developed the science of
ballistics. Tartaglia was
determined to discover the ideal firing angle to achieve a maximum range. He experimented with a variety of
cannons and derived the correct answer of 45 degrees but was also aware of many
inaccuracies in his data due to external effects (such as drag). Tartaglia, who had experimented with
almost every type of cannon in existence in Europe, had a great deal of data on
cannons and so was able to develop the first ballistic firing tables; these
tables were instrumental in educating gunners and developing artillery as a
precise military tool.
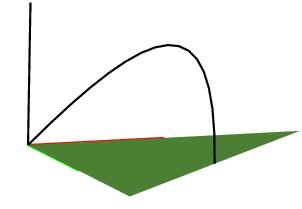
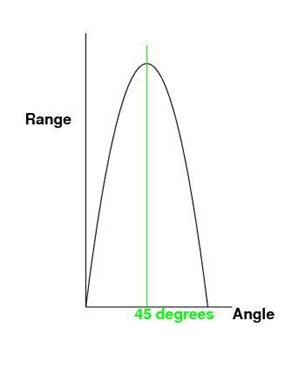 Range is maximized by a 45 degree
firing angle.
Range is maximized by a 45 degree
firing angle. 
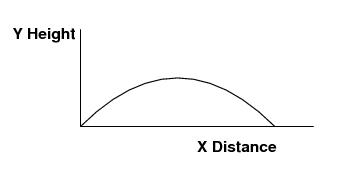
The next major
contribution to ballistics came from Galileo Galilei who showed that the
acceleration due to gravity is the same for all objects and air drag was the
factor that changed their descent velocities. He was able to determine that ballistic
trajectories are parabolic. He
theorized that the velocity of a projectile was related to the drag acting upon
the projectile but erroneously assumed that gravity a greater effect that
drag. He lacked the ability to
ascertain the effects of drag at high speed and so was unable to measure how
air drag retards a projectiles velocity.
The ability to
measure the velocity of a projectile and therefore study the effects of drag
was not conceived till 1730 when Englishman, Benjamin Robbins, invented the
Ballistic Pendulum. The ballistic
pendulum is essentially a block of wood suspended from a string. The projectile is fired horizontally
into the block of wood. The maximum
angle and the height to which the block swing allow their speed and momentum to
be calculated. From this data, the
blocks momentum and its speed just before impact can be easily determined. Robbins found both the initial velocity
of a projectile and also the change in velocity over considerable distances. He was able to observe the incredible
deceleration of a high speed projectile and found that drag affected a
projectile 50 – 100 times more than gravity.
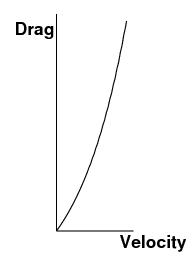
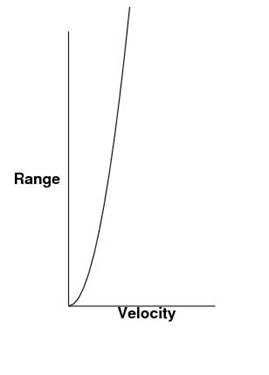 A
drag free environment would have an exponential range function.
A
drag free environment would have an exponential range function.
Sir Isaac
Newton made the most important contributions to ballistics and the study of
aerodynamic drag. In Principia, he
derived formulas and explained the mechanics of ballistics. He concluded that the retarding force
(drag) that acts on a projectile through air is proportional to the density of
air, the cross sectional area of the projectile and approximately the square of
its velocity. This relationship
holds fairly well even now for objects well below the speed of sound.
Leonard Euler tried (with some success) to solve the complex trajectories of ballistic flight. He developed the Euler method mainly to simplify ballistic equations and integrate the various stages of a flight path into one. The formulas that follow are along those lines of simplified trajectories.
Modern Ballistic Theory
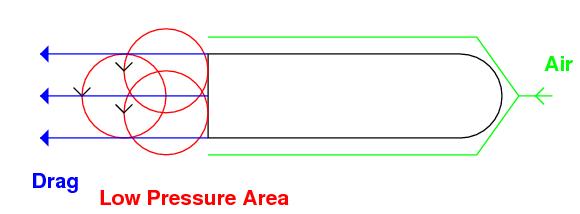
Aerodynamic
drag involves two forces: that of air pressure drag and that of skin
friction. Air pressure drag is
caused by the fact that an object disturbs the air flowing around it, causing the
air to separate from the objects surface.
Areas of low pressure form behind the object that result in a pressure
drag on the object, essentially pulling the object backwards. Skin friction drag occurs where the air
comes into contact with the surface of the object and is less of a factor than
air pressure drag.
The difficulty is to express
drag as a function related to the known ballistics equations.
![]()
Where V is velocity and and A
is deceleration due to drag.
F is a constant for a
particular projectile and so must be derived and recalculated for each
projectile and muzzle velocity (the velocity at which a projectile leaves the
artillery.)
F is c times the small range
interval in which a projectile loses 1/c of its remaining speed due to drag.
Example:
F = 2700 (which means for
every 27 meters, the projectile loses 1% of its velocity)
Say a projectile is fired at 1000
m/s, after traveling 27 meters, it will have had its velocity reduced to 0.99
(1000) = 990 meters and so on such that:
![]() Where r is the
distance traveled.
Where r is the
distance traveled.
F can be calculated by
comparing two velocities at two points:
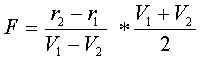
F is modeled proportional to
V raised to a power n such that: ![]()
To find n, values of F are
needed at two velocities and two ranges.
One can then use:
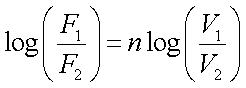 to find n.
to find n.
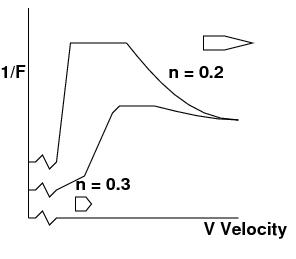 We
see two sets of experimentally determined retardation coefficients based on two
different caliber bullets. The n
values are approximated.
We
see two sets of experimentally determined retardation coefficients based on two
different caliber bullets. The n
values are approximated.
The peaks reflect when the projectiles pass through the sound barrier where they attain their maximum drag.
Gravity
can be ignored when compared with drag when velocity is considered.
Eg: On a horizontal trajectory over 300
yards, gravity causes 10 fps of downward velocity in relation to the original
vector while drag reduces the horizontal velocity by 630 fps (considering an
average retardation coefficient.) So using the Pythagorean theorem: ![]()
Hence gravity can be
essentially ignored.
Drag Changing as Velocity Decreases
Drag reduces
as the velocity decreases so the easiest way to calculate this change is to
recalculate the drag over several intervals. In general, the greatest percentage of
velocity is lost over a short period of time but a large distance and then the
change in distance over time reverses (longer time at a given range of velocity
but shorter distance.)
Comparing Flight Times of a Projectile using either a
Series of Steps or using one Interval
The formula
for computing flight time over a distance using drag is:
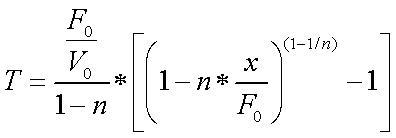
Where ![]() are the initial
retardation coefficient and the initial velocity.
are the initial
retardation coefficient and the initial velocity.
This was the area Euler made
his greatest developments in the field of ballistics.
With ![]() set at 3000 fps,
set at 3000 fps, ![]() set at 4000, n
starting at 0.5 and x = 1200 feet.
With n remaining the same, T = 0.46194 seconds, with three changes of n
as the velocity lowers (n =1/3, n =1/5 and n =0), T only changes by 0.00013
seconds or an 0.028% difference.
set at 4000, n
starting at 0.5 and x = 1200 feet.
With n remaining the same, T = 0.46194 seconds, with three changes of n
as the velocity lowers (n =1/3, n =1/5 and n =0), T only changes by 0.00013
seconds or an 0.028% difference.
The wind effects a projectile
with the following relation:
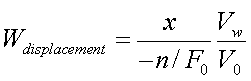 where
where ![]() is the velocity of the wind.
is the velocity of the wind.
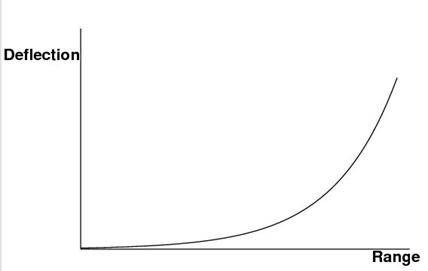 Shows
the increase in deflection (cm) as range increases (m)
Shows
the increase in deflection (cm) as range increases (m)
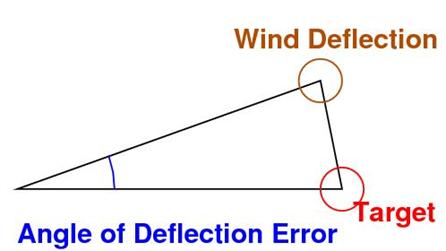
Knowing the deflection that
the wind will cause, one can then use the angle at which the wind is at to
determine where the wind will direct the projectile.
 The
Wind angle is the direction of the wind with relation to the original ballistic
path.
The
Wind angle is the direction of the wind with relation to the original ballistic
path.
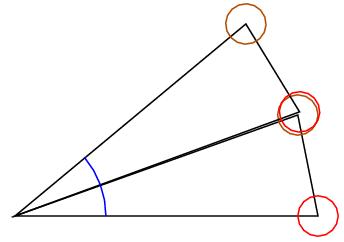 By
rotating the ballistic launcher by the angle of deflection error, just
have to alter range slightly to hit target.
By
rotating the ballistic launcher by the angle of deflection error, just
have to alter range slightly to hit target.
Moving Target
The
hitting of a moving target is actually simple than one would at first assume as
long as the target is on a predictable path with an observable velocity; the
key is to fire to lead a target to the correct distance. This lead is just distance that the
target will cover during the time taken for the projectile to reach its
target. In order to do this, one
must calculate the flight time (which has already been shown above) and then
multiply that by the target’s own velocity.
Eg. Muzzle velocity of 3000
fps, target at 400 yards and moving at 50 km/h or 44 fps (very close, but we
can imagine a tank versus tank battle where a moving target would be
important,) then the time to target would be T = 0.47 seconds. So: ![]() and so would have to fired
20.7 feet in front of the moving target.
and so would have to fired
20.7 feet in front of the moving target.
Ballistics Today
 3d
representation using Bezier curves
3d
representation using Bezier curves
Today, every gun of any size
or shape (whether battleship or air rifle) has had its ballistics analyzed to
determine every possible variable.
All this data is then put into vast spread sheets and a ballistics computer
breaks the data down into several categories.
-Muzzle Velocity
-Projectile Mass
-Projectile Shape Class (What
is it)
-Distance to target
-Wind speed and direction
-Target velocity
-Temperature
-Altitude
The computer then finds the
ideal firing sets based on pre-established data and returns that data.
The science of
ballistics has not changed much in the last 300 years from the point of view of
the person firing the artillery.
They are still just inputting data into a firing table (though now
computerized) and using that data to fire at a target. The science of ballistics has evolved
though as a greater study of the atmospheric conditions and the affects of drag
at higher speeds. The X-1 (the
first manned object to surpass the sound barrier) was designed to look like a
bullet with control surfaces mainly because it was known that a bullet could
exceed the sound barrier but not why.
Modern ballistics is all about designed a projectile that resists drag
at its prescribed flight profile (e.g. Supersonic vs. subsonic) rather than
getting to the target.
Created by: John P Knox 79314019
For: Math
308 Final Project: Professor Bill Casselman
Last Edited: December 16th, 2005