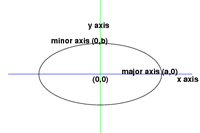
The path that the planets and even comets make around the sun are known to be elliptical. The most common equation for describing an ellipse is

x^2/a^2 + y^2/b^2 = 1

where a is the major radius and b is the minor radius with the origin being in the center of the ellipse

the parameterize version of this equation is

x = a cos ø, y = b sin ø

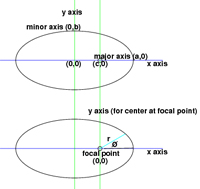
However these equations are unpractical. The sun does not reside at the center of the orbit but at one of the foci. the equation has to be modified so that the origin is positioned at the sun's center. Another point is that instead of using the minor radius b to help describe the orbit, it is better to use the eccentricity, e of the ellipse where

e = (1 - b^2/a^2)^(1/2)

Eccentricity describes the shape of the ellipse. When eccentricity is nearer to 1 the ellipse is flattened, more cigar shaped; when the eccentricity is nearer 0 it gives a more circular shape.

To find the focal point c, the initial equation is

c = ea = (1 - b^2/a^2)^(1/2)

Now using all the above equations, the polar cordinates that describe the ellipse with the origin at the focus is

r = a (1 - e^2)/(1 + e cosø), where r is radius from the focus

and the parameterize version of this equation is

x = a cos ø - e, y = a (1 - e^2)^(1/2) sin ø

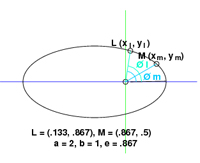
Starting with a 2-D scenerio, it takes two points on the path to find the major radius and eccentricity of the path of the orbiting body

L(xl,yl) and M(xm,ym) where

xl = a cos øl - e, øl = tan^-1(yl/xl) and

xm = a cos øm - e, øm = tan^-1(ym/xm)

from these four equations

a = (xm - xl)/(cos øm - cos øl)

and

e = (cos øm - xm)(xm - xl)/(cos øm - xm)

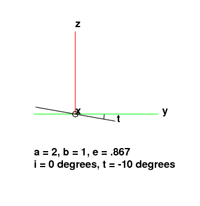
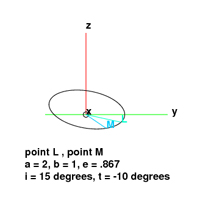
Now in 3-D, the ellipse can be inclined and/or tilted. Inclination, i is the rotation about the y-axis and tilt, t is the rotation about the x-axis. Again only two points are needed to find the major radius, eccentricity, inclination, and tilt of the path of the orbiting body, with one caveat, that both points are not at the minor radius, otherwise another point will need to be included.

To find the inclination of the path of the orbiting body, the normal, n of the plane that the ellipse resides on needs to be found. this can be done by using the cross product. Using the points L(xl,yl,zl ) and M(xm,ym,zm) and the origin, two vectors, u and v, can be created.

u = (-xl,-yl,-zl), v = (xm,ym,zm)

The normal is the outcome of taking the cross product of these two vectors divided by the lenght on the cross product.

n = u X v = [ x,y,z ; -xl,-yl,-zl ; xm,ym,zm ]

n = ((-yl)(zm)-(-zl)(ym), -(-xl)(zm)-(-zl)(xm), (xl)(ym)-(-yl)(xm))

and length of the normal,

p = ((((-yl)(zm)-(-zl)(ym))^2 +(-(-xl)(zm)-(-zl)(xm))^2 + ((xl)(ym)-(-yl)(xm))^2)^(1/2)

i = cos^-1(((xl)(ym)-(-yl)(xm))/p)

The tilt can be found by finding the angle between one of the vectors and its projection onto the y-z plane using the cosine law, just as long as that vector is not along the x-axis. the project of L (xl, yl, zl) onto the y-z plane is (0, yl, zl) and the vector that describes the y-z plane is (0, -1, 0)

t = cos^-1((0, -1, 0) • (0, yl, zl)/((yl^2 + zl^2)^(1/2))

So only two points and the focus are needed to find

major radius, a = (xm - xl)/(cos øm - cos øl)

eccentricity, e = (cos øm - xm)(xm - xl)/(cos øm - xm)

inclination, i = cos^-1(((xl)(ym)-(-yl)(xm))/p)

tilt, t = cos^-1((0, -1, 0) • (0, yl, zl)/((yl^2 + zl^2)^(1/2))

to describe the path of a celestial body orbiting the sun