ICOSAHEDRON



See the icosahedron rotating around the x, y, z axis.
Properties of the Icosahedron
  • Faces: 20 triangles
  • Vertices: 12, each with 5 edges meeting
  • Edges: 30
  • Dihedral angle: 138°11'
    • The Symmetry
    Surface Area

    The surface area of an icosahedron is made up of 20 regular triangles.
    Volume
    One way of calculating the volume: the octahedron can be divided into 20 tetrahedra.
    Each can be calculated using the pyramid method.
    To get the vertices, take a look at this picture:

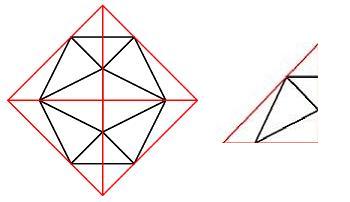
    Each vertex of the icosahedron lies on the edge of octahedron,
    is divided into 2 lines with the golden mean ratio Ø.
    Another way to calculate the volume is divide the icosahedron into 3 parts.
    The top part: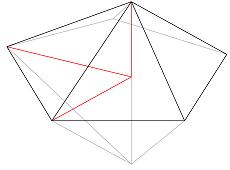
    The angle between the two red lines on the pentagon is 360/5=72°. Let r = radius of the pentagon, a = length of edge, by the cosine law:
    a² = r² + r ² - 2r²cos(72°)
    The height of the pyramid is calculated by the Pythagoras theorem. h² = r² + a².
    The bottom part of the icosahedron is the same.
    The top view of the middle piece: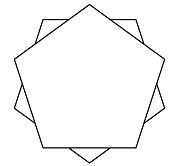
    V = [5 × (3 + √5) / 12]a³